Welcome to Educational Designer #16
This issue includes articles on many aspects of educational design, from the design of hands-on lessons suitable for huge classes in open-air classrooms in Africa, to university courses and school assessment using sophisticated technology tools.
The first article is by Charles Lovitt, the winner of the 2021 ISDDE Prize, drawing on his early experiences as a teacher. He recounts how he taught powerful numerical methods to early algebra students, which fostered confidence and success but seem to be ignored in decades of subsequent curriculum revisions. Brian Gane, Diksha Gaur, Samuel Arnold & Daniel Damelin present a framework for designing assessment of multiple dimensions of science learning, and illustrate challenges and successes with examples such as the distribution of water on earth. Dominika Majewska, Rachael Horsman and Janine Angove report on a collaboration to guide the redevelopment of lessons from Australia to meet US curriculum standards by mapping features such as the flow of ideas and whether all key concepts were well covered. Ian Lowe reports on his personal mission to use his expertise to help reduce educational inequality and enhance mathematics learning in Malawi. He designed hands-on lessons using very simple materials to improve learning in very large classes. Katie Stripe outlines how a short not-for-credit course designed for post-graduate students in one faculty has been able to be efficiently adapted to meet the needs of students from many different parts of the university by combining generic and bespoke faculty-specific skills, and incorporating digital personae for the interactive and reflective components. Leah Rosenbaum, Paul Reimer, Alik Palatnik and Dor Abrahamson describe their popular ‘Embodied Icosahedron’ activity, which is designed around body-scale movement, authentic embedding of disciplinary content within an activity, and constructionist pedagogy.
This journal depends on the hard work of volunteers - the editorial team and anonymous reviewers and especially to Daniel Pead our design editor who maintains the journal website and creates each issue and to the new associate editor Róisín Neururer. As this is my last issue as Editor in Chief, I thank the members of all the editorial teams since 2016 for their promptness, their sound advice and their insights into how excellence in educational design can be promoted by this journal. I also thank all the authors who have shared their innovative ideas and made editing this journal such a pleasure for me.
The editorial team hopes that readers will benefit from seeing the many possibilities for educational design showcased in this issue,
Kaye Stacey
Editor in Chief
A note from the design editor: First, I would like to offer my own thanks and best wishes to Kaye, who, as well as being a meticulous editor – helping to make my part of the job a pleasure – has played a vital role in encouraging and supporting authors.
Sadly, as this issue was in the last stages of production, I received the news that Hugh Burkhardt – who was a driving force behind the creation of both the ISDDE and this journal – had died suddenly at the age of 88. He was a persistent campaigner in the drive to improve mathematics education and assessment, both through his own work and his efforts in finding and nurturing new designers. Hugh, Susan McKenney and myself assembled and edited the first issue of Educational Designer in 2008 with the aim of raising the academic profile of the “research & development” of teaching materials and practices. He will be greatly missed.
Daniel Pead
Design Editor
Numerical Methods – A Curriculum Mystery

Read article
This opinion paper explores and questions why numerical (iterative) methods, so widely used in business and scientific endeavours, are largely underrepresented in school mathematics curricula. Mathematics topics such as solving quadratic equations by using the quadratic formula or using algebraic procedures to solve problems in measurement, geometry or probability are deeply entrenched in the teaching strategies employed by teachers and in the resources developed to support those behaviours. Iterative approaches to the same topics offer an alternative, and in many instances more efficient, approach. They are often more suited to struggling students and can lead to greater success and deeper understanding of the underlying mathematical concepts. Classroom examples are offered, the potential advantages discussed, and finally some thoughts are given on why in this digital STEM age numerical approaches have not penetrated school curricula to the extent they could or should.
Lovitt, C.
Numerical Methods – A Curriculum Mystery.
Educational Designer, 4(16). ISSN 1759-1325
http://www.educationaldesigner.org/ed/volume4/issue16/article61/
Multidimensional Science Assessment: Design Challenges and Technology Affordances
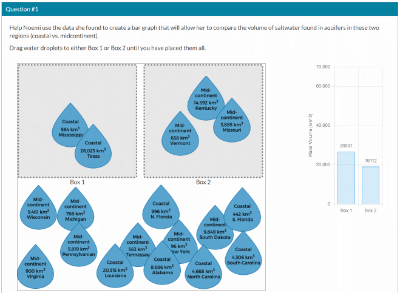
Read article
Contemporary views on what students should learn increasingly emphasize that students need to acquire more than a base of knowledge; they need to acquire the skills and abilities to use such knowledge in dynamic and flexible ways. To be most effective, learning environments need assessments that are aligned to these perspectives. Using a principled design framework can help guide assessment development toward such targets. Even when using a framework, however, thorny design challenges may arise. Technology-enhanced assessments offer opportunities to overcome such challenges but are not a solution in and of themselves and can also introduce new challenges. In this paper, we describe three challenges (conflict between multiple dimensions of science proficiency, authentic data, and grade-appropriate graphing tools) that we faced when designing for a specific Next Generation Science Standard, and the theoretical and design principles that guided us as we ideated design solutions. Through these designs we maintained alignment to our multidimensional assessment targets, a critical component of our larger assessment validity argument.
Gane, B.D., Gaur, D., Arnold, S., Damelin, D. (2024).
Multidimensional science assessment: Design challenges and technology affordances.
Educational Designer, 4(16). ISSN 1759-1325
Retrieved from:
http://www.educationaldesigner.org/ed/volume4/issue16/article62/
Mapping HOTmaths Lessons to the Common Core State Standards for Mathematics
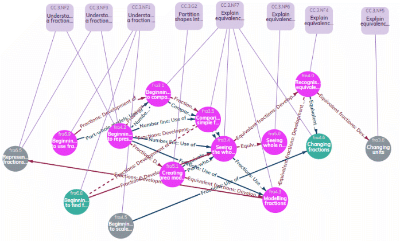
Read article
This article reports on a collaborative project between Cambridge Mathematics and HOTmaths, where the Cambridge Mathematics Framework was used to map HOTmaths fraction lessons to the fractions content in the USA’s Common Core State Standards for Mathematics, with focus on grades 3-8. This article describes the project, the processes involved in training the HOTmaths team to use the Cambridge Mathematics Framework to map their content onto the Common Core State Standards, and outcomes of the collaboration, such as using the mappings to identify places where HOTmaths lessons did not flow well. The article also gives some recommendations for future research.
Majewska, D., Horsman, R., Angove, J. (2024).
Mapping HOTmaths Lessons to the Common Core State Standards for Mathematics.
Educational Designer, 4(16). ISSN 1759-1325
Retrieved from:
http://www.educationaldesigner.org/ed/volume4/issue16/article63/
Hands-on Mathematics Activities in Malawian Primary Schools

Read article
Because of large class sizes and very few resources for schools, most classrooms in Malawi are dominated by teacher talk and pupils find learning mathematics hard. This article describes the outcomes of the author’s research and practical experiences in Malawi developing hands-on mathematics activities to increase conceptual understanding, problem solving, skills and engagement in this difficult context. After initial research in Malawian classrooms, the author achieved considerable success over five years in teacher in-service courses where teachers had first-hand experience of working together in small groups with hands-on materials. Simple, inexpensive, and effective hands-on materials made from paper and using playing cards are described. There is an impressive report of a teacher taking these methods back to her school. Small groups helped students learn from and support each other, often using the local language before formal English words are introduced. Even in large classes such as those in Malawi, carefully designed hands-on teaching activities using small group work are manageable.
Lowe, I. (2024).
Hands-on Mathematics Activities in Malawian Primary Schools.
Educational Designer, 4(16). ISSN 1759-1325
Retrieved from:
http://www.educationaldesigner.org/ed/volume4/issue16/article64/
Bespoke Learning Design – One Course, Multiple Cohorts
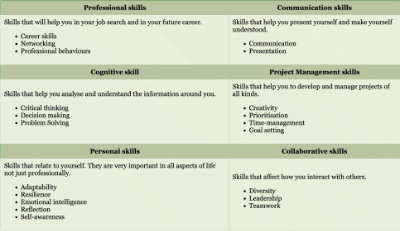
Read article
Creating content that is relevant and appropriate for specific cohorts of students is practically impossible to do at an institutional scale. Creating content on a faculty or departmental level gives much greater scope for a bespoke programme that addresses students’ needs but offers different challenges of scale and support. This paper describes how a cohort-specific course was developed and scaled up using a process whereby the bespoke elements of it could be easily modified and then combined with generic content to create a suite of courses that are easily managed, scalable, and provide tailored content to a variety of student groups.
Stripe, K. (2024).
Bespoke Learning Design – One Course, Multiple Cohorts.
Educational Designer, 4(16). ISSN 1759-1325
Retrieved from:
http://www.educationaldesigner.org/ed/volume4/issue16/article65/
Building Mathematical Spaces Through Multi-Faceted, Body-Scale Geometry

Read article
In the course of conducting educational design research, new learning activities may emerge, sometimes serendipitously, that resonate with educators’ intuitive understandings of what learning could and should be like. Articulating these activities’ ‘secret sauce’ could enable the creation of similar educational activities. This article examines one such activity from mathematics education research, the Embodied Icosahedron activity, which numerous practitioners have described as an ideal mathematics learning experience. To characterize the activity’s appeal, we first document how this activity was disseminated across education research, teacher education, professional development, classroom, and community settings. Next, we present and analyze interviews with educators who facilitated the activity in each of these educational contexts. At the intersection of these multiple testimonies, analysis reveals, is a shared appreciation of three design qualities: body-scale movement, authentic embedding of disciplinary content within an activity, and realizations of constructionist pedagogical philosophy. The realization of these qualities within a mathematics activity - a domain renowned for its reputation as abstract, impersonal, and boring - suggests a particularly promising approach to educational design. To achieve inclusive, empowering mathematics education, we speculate, we should pursue the design of authentic tasks at the intersection of mathematics and existing practices that already engender those types of transformative interaction.
Rosenbaum, L. F., Reimer, P., Palatnik, A., Abrahamson, D. (2024).
Building Mathematical Spaces Through Multi-Faceted, Body-Scale Geometry.
Educational Designer, 4(16). ISSN 1759-1325
Retrieved from:
http://www.educationaldesigner.org/ed/volume4/issue16/article66/