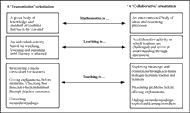
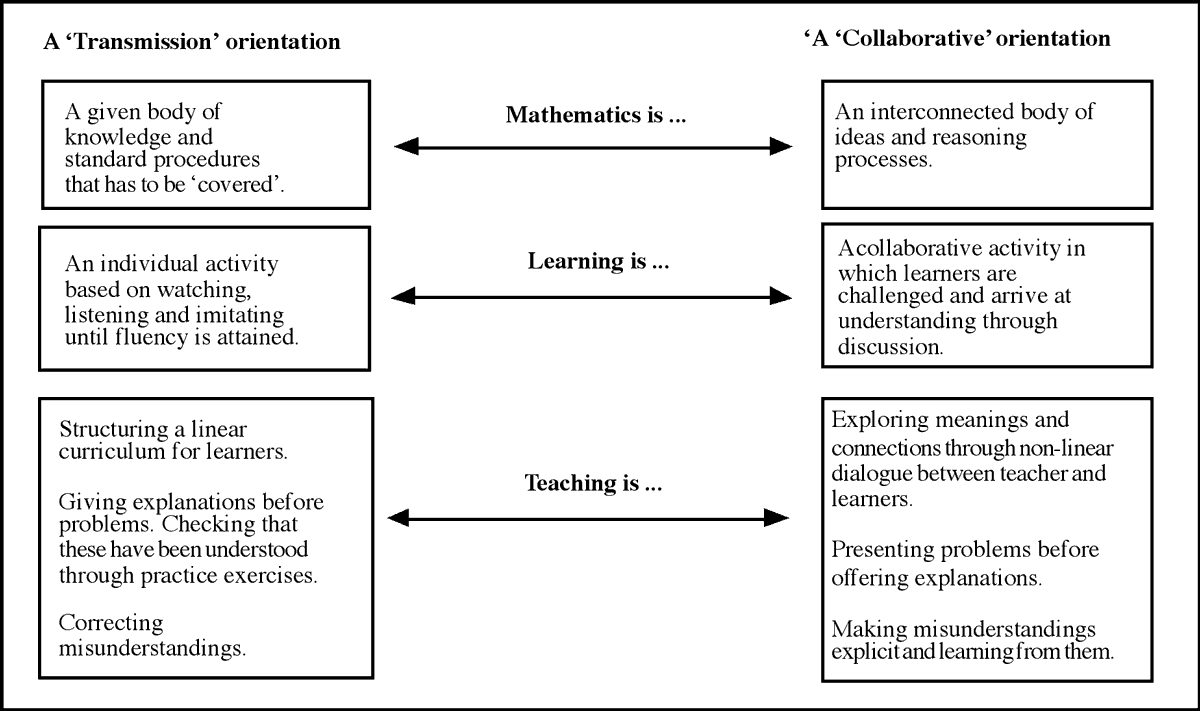
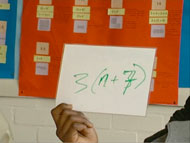These principles challenge many teachers' existing orientations towards mathematics, learning and teaching as outlined in Figure 1 (Swan, 2005). A 'transmission' orientation in which explanations, examples and exercises dominate must give way to a more collaborative orientation in which students work together on 'interconnected', 'challenging' tasks; tasks that confront common difficulties. This model of learning should not be confused with that of "discovery" teaching, where the teacher simply presents tasks and expects students to explore and discover the ideas for themselves. Here, the teacher's role includes: assessing students and making constructive use of prior knowledge; making the purposes of activities clear; challenging students through effective, probing questions; managing small group and whole class discussions; encouraging the discussion of alternative viewpoints; drawing out the important ideas in each lesson; and helping students to make connections between their ideas.

A Designer Speaks: Malcolm Swan
MARS/Shell Centre
University of Nottingham
England
Designing a Multiple Representation Learning Experience in Secondary Algebra
Abstract
1This paper describes some of the research-based principles that I use when designing learning experiences to foster conceptual understanding. These principles are illustrated through the discussion of one type of experience: that of sorting multiple representations. I refer to learning experiences rather than tasks, because tasks are only one component of the design. Close attention is also paid to the role of the teacher in creating an appropriate climate for learning to take place.
After a brief excursion into my own theoretical framework, I describe the educational objectives behind my design and provide a detailed explanation of it in one topic, that of algebraic notation. This is followed with an explanation of the principles that informed the design and the evolution of the task. Finally, I briefly indicate how the design might be generalised to include other topics.
Introduction
2My own designs for novel learning experiences are based on a three-way analysis of: the purposes they are intended to serve; the learning theories related to those purposes; and the empirically tested principles for design that emerge from these theories. Clearly, different learning theories apply when different learning outcomes are desired. A full analysis of these purposes, theories and principles is available in Swan (2006a).
There are perhaps five distinct purposes for learning mathematics: (i) developing fluency when recalling facts and performing skills; (ii) interpreting concepts and representations; (iii) developing strategies for investigation and problem solving; (iv) awareness of the nature and values of the educational system and (v) an appreciation of the power of mathematics in society (e.g. Cockcroft, 1982; NCTM, 1988; Stigler, Gonzales, Kawanaka, Knoll, & Serrano, 1999; Stigler & Hiebert, 1999). In the examples described below, my purpose is conceptual.
The learning theories I adopt for this purpose are derived from the social constructivists: concepts are co-created as language and symbols are appropriated and internalised (Bakhtin, 1981; Vygotsky, 1996). Collaborative discussion is therefore essential. Other relevant design principles include the importance of focusing directly on significant conceptual obstacles (Bell, 1993; Wigley, 1994); building on the knowledge students already have (Black & Wiliam, 1998); creating tension and cognitive conflict that may be resolved through discussion (Bell, 1993; A Bell, Swan, Onslow, Pratt, & Purdy, 1985; Brousseau, 1997); using tasks that are 'accessible, extendable, encourage decision-making, creativity and higher order questioning' (Ahmed, 1987); using multiple representations to create connections (Askew, Brown, Rhodes, Johnson, & Wiliam, 1997); and using tasks that allow students to shift roles and explain and teach one another (Bell, Swan, Crust, & Shannon, 1993b).
Of course, principles guide rather than determine a design; the quality of the outcome also involves both creative input, based on prior experience and imaginative extensions from it, and systematic development through feedback from trials. These are much more difficult to describe.
In coming to understand a concept, a student must single it out and bring it to the forefront of attention (identify); notice similarities and differences between this concept and other similar ones (discriminate); identify general properties of the concept in particular cases of it (generalise) and begins to perceive a unifying principle (synthesise) (Sierpinska, 1994). Working with teachers, I have developed five task 'types' that encourage these processes (Table 1).
| Classifying mathematical objects |
Students devise their own classifications for mathematical objects, and/or apply classifications devised by others. In doing this, they learn to discriminate carefully and recognise the properties of objects. They also develop mathematical language and definitions. The objects might be anything from shapes to quadratic equations. |
|---|---|
| Interpreting multiple representations |
Students work together matching cards that show different representations of the same mathematical idea. They draw links between representations and develop new mental images for concepts. |
| Evaluating mathematical statements |
Students decide whether given statements are always, sometimes
or never true. They are encouraged to develop mathematical arguments
and justifications, and devise examples and counterexamples to defend
their reasoning. For example, is the following statement always,
sometimes or never true? If sometimes, then when? |
| Creating problems |
Students are asked to create problems for other students to
solve. When the 'solver' becomes stuck, the problem 'creators' take on
the role of teacher and explainer. In these activities, the 'doing'
and 'undoing' processes of mathematics are exemplified. |
| Analysing reasoning and solutions |
Students compare different methods for doing a problem, organise solutions and/ or diagnose the causes of errors in solutions. They begin to recognise that there are alternative pathways through a problem, and develop their own chains of reasoning. |
The educational objectives of the design.
3I now describe a specific example of one of the task types, "Interpreting multiple representations". In this task, students sort cards showing alternative representations of algebraic expressions into sets, so that each set has equivalent meaning. In so doing, students must discriminate between commonly confused expressions and explain their differences. This task focuses on an aspect of mathematics content that is often taught, with limited success, in a mechanistic manner: the interpretation and manipulation of algebraic expressions. In particular, it involves: translating between algebraic expressions words, tables, and geometrical areas; recognising the order of arithmetic operations implied by conventional notation; recognising equivalent expessions; using the distributive laws of multiplication and division over addition. The design is taken from a nationally distributed resource for teachers (DfES, 2005), and was developed as part of a research project with low-attaining 16-19 year old students in Further Education Colleges (Swan, 2006a; Swan & Green, 2002).
An outline of the design
4The preparation for the lesson involves enlarging and cutting out sets of cards (Figure 3) so that they may be easily viewed by groups of 2 to 4 students. Before beginning the task, the teacher asks students to respond to a few algebra questions on paper, without consultation. These answers are not discussed, but are put to one side. The teacher explains that they will be reconsidered to at the end of the session. The purpose of these is to help students become aware of any changes in their own thinking. These questions are of the form:
What does 4(x+5) mean? Does it mean the same thing as 4x+5? If not what is the difference?
What does (5x)2 mean? Does it mean the same thing as 5x2? If not what is the difference?
What does (x+6)2 mean? Does it mean the same thing as x2+62? If not what is the difference?
Next, the teacher asks the students a few oral questions, to assess how well they can translate between words and symbols. Students present their answers using 'mini-whiteboards'. These are small, easily erasable laminated boards (Figure 2). Their advantage is that the teacher can rapidly assess many responses.
Show me an algebraic expression that means:
Add 7 to n, then multiply your answer by 3;
Multiply n by 3, then add 7;
Add 2 to n, then divide your answer by 4;
Multiply n by n, then multiply your answer by 4;
Multiply n by 6, then square your answer.
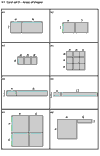
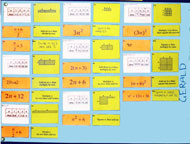
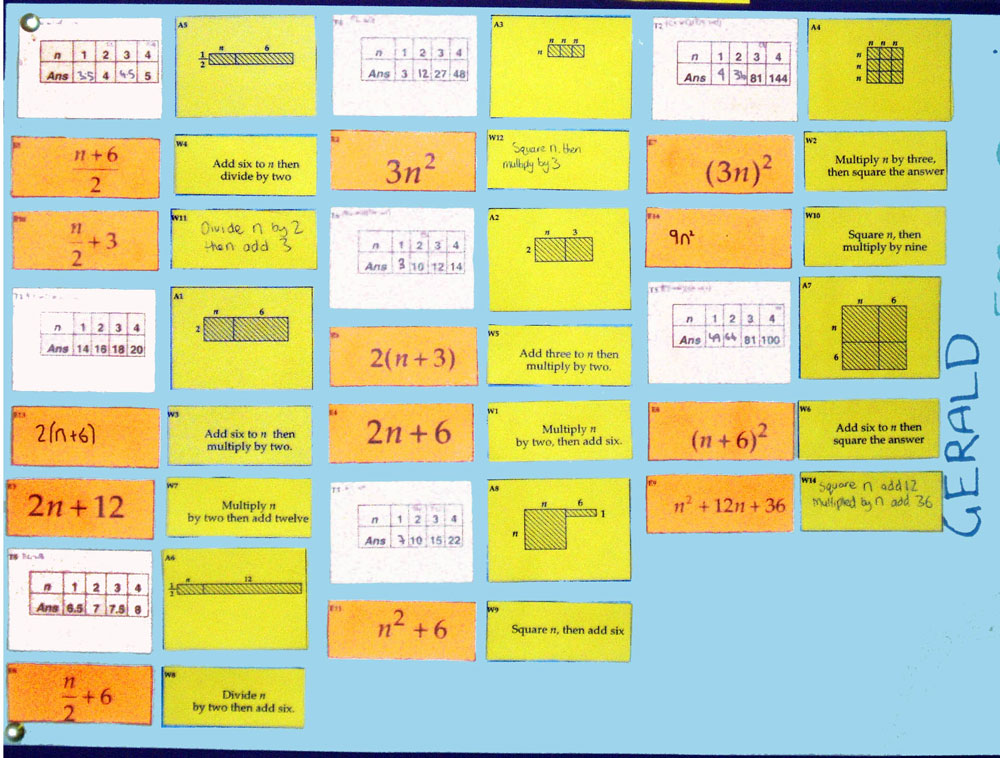
Students now work in groups. The set of cards (Figure 3) are presented in three stages.
| Figure 3: Cards for matching (DfES 2005) | |||
|---|---|---|---|
| Figure 3: Cards for matching (DfES 2005) | |||
|---|---|---|---|
 |
 |
||
 |
 |
||
First, students take it in turns to match the algebraic expressions to the written explanations. As they do this, they must lay the cards out side-by-side on the table. This activity forces students to attend to the order of operations. (So for example, students must discriminate between "Add six to n then multiply by two" from "multiply n by two then add six"). Students use the blank cards to produce additional expressions or explanations when they cannot find ones to match. Some students may notice that some expressions are equivalent, e.g. 2(n+3) and 2n+6. This is not commented on this at this stage.
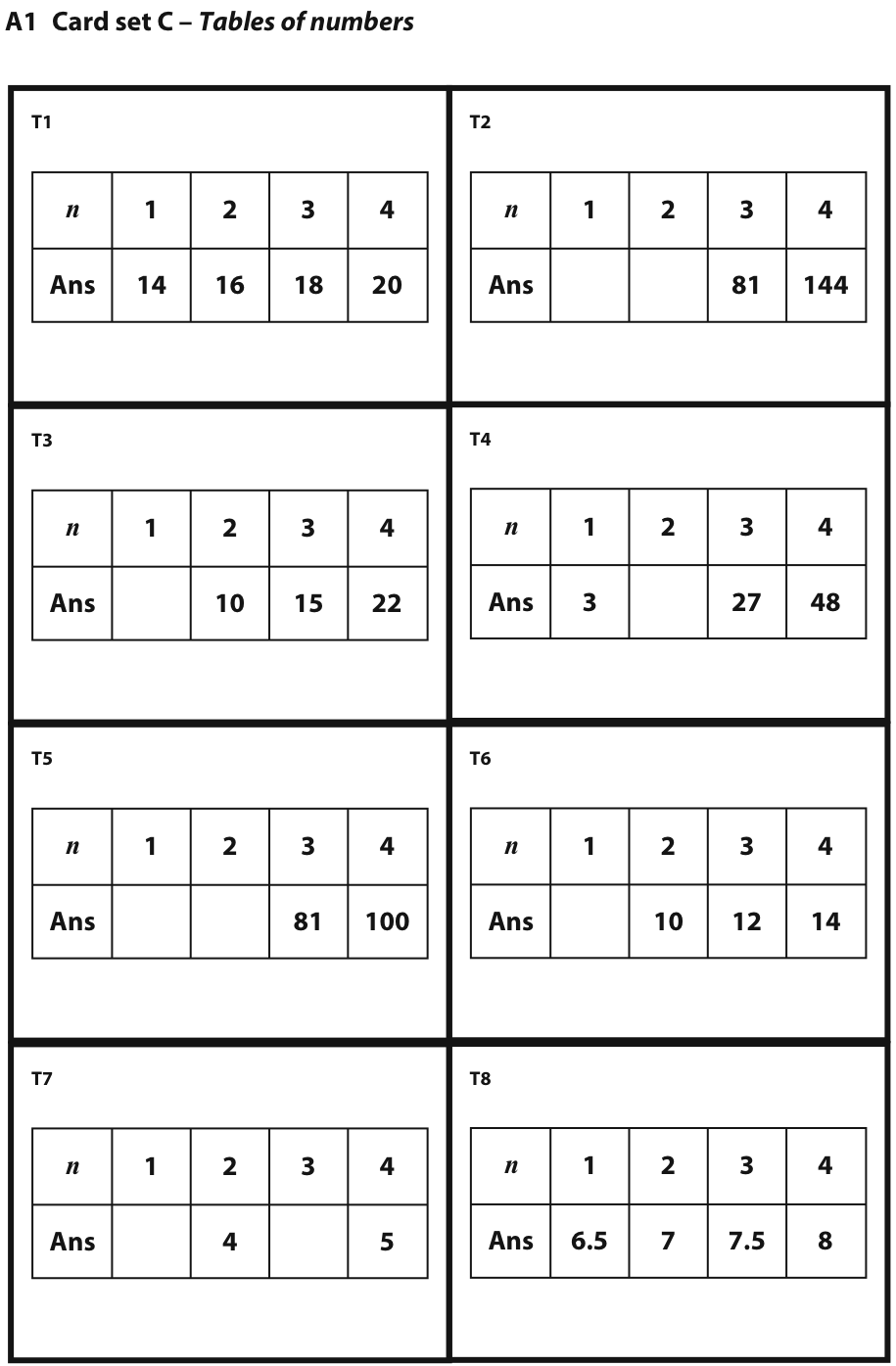
Secondly, students are given the cards showing tables of numbers. This time, there are no blank cards, but there are gaps in the tables that need completing. These ensure that students continue to make connections after matching.
Very soon, students complain that there are not enough of these cards for one-to-one matching and then, more slowly, begin to notice that in some cases, different expressions correspond to the same table, such as 2(n+3) and 2n+6; (n+6)/2 and n/2+3; (3n)2 and 9n2. At this stage, they have no explanation for this, it is simply an observation. The teacher encourages students to test these equivalences using other values for n, including very large numbers, decimal numbers and fractions: "Does this always match, even when you choose n = 250? n = 2.6? n = 1/3?"
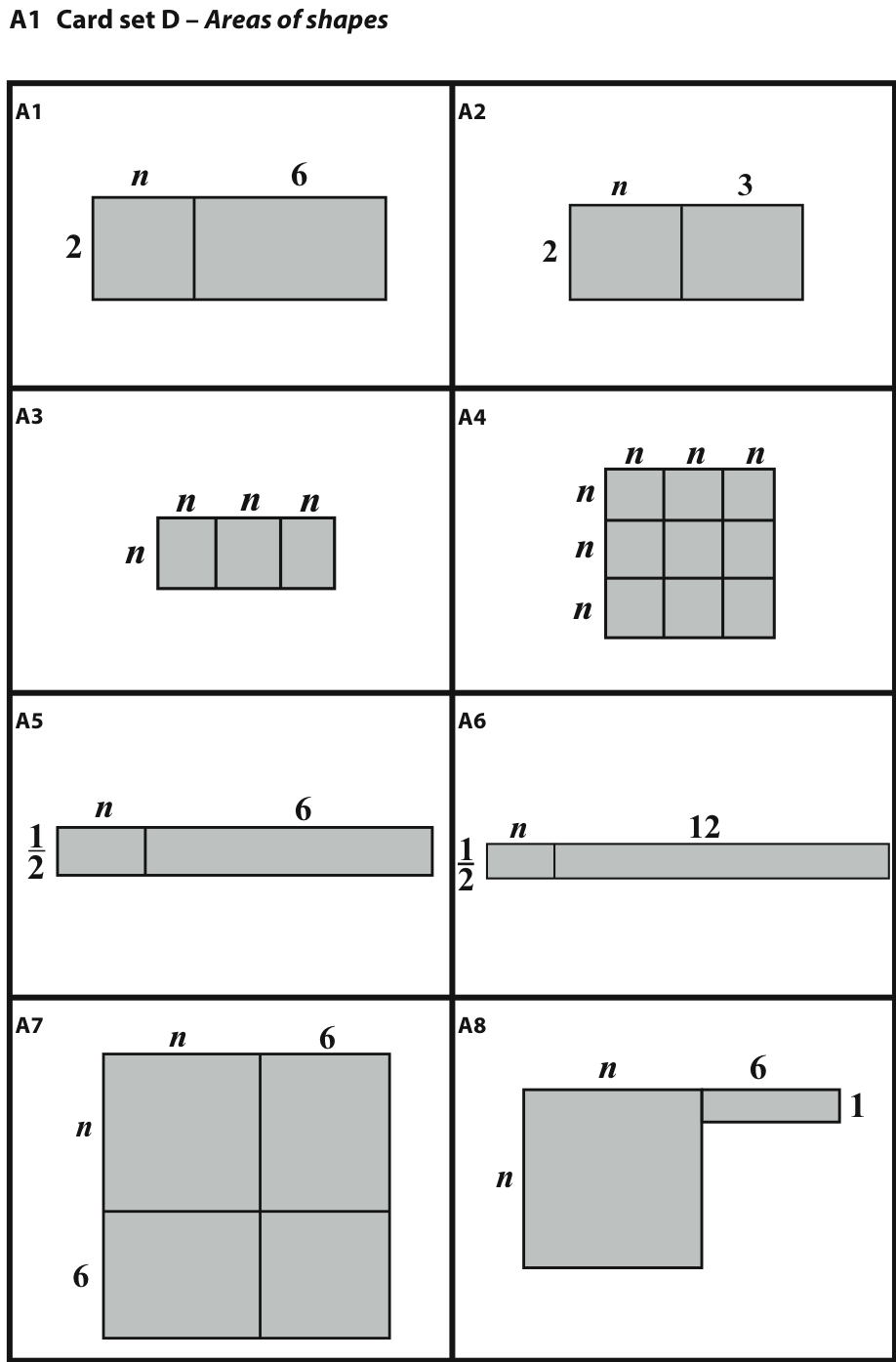
Thirdly, students are issued with the area cards and match these to the other cards, using the areas of these pictures to explain why different pairs of expressions might be equivalent. They do this by arranging the matching groups of cards onto posters and writing explanations alongside (Figure 4). Throughout this process, the teacher prompts students to make connections between representations: "How can you see that this area matches this expression directly?", "How can you see that these words match this table directly?"
A plenary discussion is now held in which the teacher encourages
students seeks to assess and generalise what they have discovered, using
further questioning. For example:
Draw me an area that shows this expression: 2(n+3).
Write me a different expression that gives the same area.
Now draw me an area that shows this expression: 4(x-7).
Finally, students revisit their answers to the questions that were asked at the very beginning of the session and (i) correct their work, (ii) describe the causes of their mistakes.
| Movies (from Swan & Green, 2002) | |
|---|---|
Movie 1:
Matching Cards  Click
to play Click
to play
This movie shows three students in discussion with the teacher. This class is a 16-19 year-old group of low-attaining students retaking Mathematics at an FE college. |
Movie 2:
Extending and Generalising  Click
to play Click
to play
This movie shows the end of a lesson, where the teacher tries to extend what students have discovered. |
Design principles that informed the design
5The following principles have been developed from my own research and a recent consultation with 150 mathematics educators (Swan, 2005; Swan & Lacey, 2008). These principles may be realised in the design, when it is faithfully implemented.
Teaching for conceptual understanding is more effective when we:
| Ground rules for students |
The role of the teacher. |
|---|---|
|
|
The process of the design
6In this section, I describe the process of designing the activity. The design presented here evolved from earlier versions, and no doubt will continue to evolve. In this case the final version (Figure 3) is similar to the first version (Figure 5) in many respects. The cards were originally devised to show combinations of symbols n, 2, 3, 6, together with pairs of operations add, multiply, divide and square. For each card, e.g. 2(n+3), an equivalent expression was devised, 2n+6, so that equivalent expressions could be deduced. In addition, a distracter, 2n+3, was introduced. Cards with the operations in the reverse order were introduced, so e.g. n2+6 was accompanied by (n+6)2. The area cards provided a spatial representation of these expressions. It was felt that students could review their knowledge of area while engaging with the task and use the areas to see why two algebra expressions might be equivalent.
The original version of the activity was in booklet form with advice to the teacher to make cards, if possible. When this was tried with teachers many did not take up this suggestion and they used the resource as though it were a textbook exercise. Students worked on the activity individually, in the order presented. The students wrote cryptic answers into exercise books like: 1-I; 2-F and so on. Towards the end of the session some teachers went through the answers using this notation and there was little discussion of the underlying concepts.
The original version suggested that the teacher should suggest that students substitute a number for n (n=4) to help them search for equivalent expressions. On reflection this did not encourage students to think of the letters as representing variables. Thus tables were introduced.
The original version contained no blank cards. This led students to match the final few expressions using elimination strategies. On reflection it appeared much more profitable to encourage students to devise cards of their own. In addition, some spaces were left on the tables cards, partly to encourage students to engage in substitution and also so that matching would be less easy to spot. Interestingly, the tables now make it possible to use new strategies for matching. For example, students who recognised square numbers in the table could search for a square area. Students were also surprised to discover that several expressions could correspond to the same table.
Comparing the original design to the final one it will also be noted that:
- Of the 12 algebra expressions in the original set, I have removed two simpler ones (9n2); 2(n+6) and introduced two more complex ones (n2 +12n +36), n2+62 along with some blank cards.
- Of the written explanation cards, I have removed two: “Square n then multiply by 3” and “Divide n by 2 then add three”.The diagrams are identical and the tables are all new.
The purpose of these changes was to challenge pupils in the following ways:
- They must use the written explanations to construct the two easier expressions cards (9n2); 2(n+6); and they already have two similar ones the teacher may refer to as a model (if this becomes necessary): (3n2); 2(n+3)
- They have to use the expressions cards to construct two easier written explanation cards: “Square n then multiply by three” and “Divide n by two then add three”; and they already have two similar ones to use as a model: “Square n then multiply by nine” and “Divide n by two then add six”
- They also have to construct two more complex written explanation cards: (n2 +12n +36), n2+62
The introduction of the two more complex expression cards also gives pupils the opportunity to distinguish (n+6)2 from n2+62 (an important realisation) and, as the little poster shows in figure 5a, they may also draw a diagram to show the difference. Secondly, they have a chance to look at the the equivalence of (n+6)2 and (n2 +12n +36). So, in short they are presented with the opportunity to deduce that (n+6)2 is equivalent to (n2 +12n +36), not n2+62, and give an explanation.
In conclusion, when designing the cards, I had to carefully consider:
- The affordances and limitations of each representation;
- How the cards would be used to expose common misconceptions;
- The order in which the representations must be presented to maximise conflict and discussion;
- The criteria that students will tend to use to match cards, and how I might minimise superficial matching;
- The degree to which sets of cards can open up the possibility for generalisation.

This page invites students to interpret the meanings of algebraic expressions. They then search for expressions which are equivalent, by substituting n = 4 into each one.
You will need to emphasize that expressions are only equivalent
if they give the same answer for every possible substitution.
If possible, introduce this as a card sorting activity. (A photocopiable
sheet is included on the next page.)
Card sorting frees the students from having to write and enables
them to pay more attention to the meanings of expressions.
When they have finished arranging and rearranging the cards, they may
then like to make a permanent copy by pasting their arrangement onto a
large sheet of paper.
As students sort the expressions, listen carefully and note their difficulties.
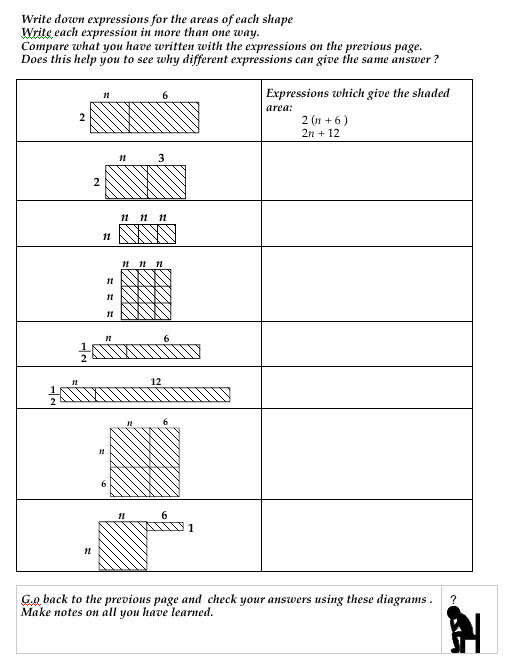
This page looks again at the same expressions, but this time links them to areas. This should help students to begin to see why different expressions are equivalent.
Ask students to match the expressions on the cards with the
shapes.
Encourage those that finish to invent additional expressions for each
shape.
Leave time for students to make notes on the important things they feel they have learned. When they have done this, ask some to read aloud what they have written and invite questions and comments from other members of the class.
Concluding remarks
7The appendix to this paper displays two further card sets that I have devised to illustrate how this task-type may be used across the mathematics curriculum. Although such complex activities pose considerable management challenges for teachers, they have been extremely popular with both teachers and students and have strongly featured in three recent projects in which I have been involved (DfES, 2005; NCEE, 2006; NRDC, 2006). The evidence from these suggests the above task types have been popular with students, have improved learning outcomes and have also had an impact on the beliefs and practices of many mathematics teachers (Swain & Swan, 2007; Swan, 2006a, 2006b, 2007).
The good thing about this was, instead of like working out of your textbook, you had to use your brain before you could go anywhere else with it. You had to actually sit down and think about it. And when you did think about it you had someone else to help you along with you if you couldn’t figure it out for yourself, so if they understood it and you didn’t they would help you out with it. If you were doing it out of a textbook you wouldn’t get that help. After I did it I found that I used a lot of brain power, but I felt dead clever. Do you know that when you have actually done something and you actually put all your effort into something.. it makes you feel dead clever. I’ve told all my friends that I have actually done a bit of work in maths. ‘Cause I never thought I was any good at maths, but I was alright with that. (Lauren, a 16-year-old low-attaining student).
Acknowledgements
8This research was funded at various stages by The Esmée Fairbairn Charitable Trust, The Learning and Skills Development Agency, and the Department for Education and Skills.
References
9Alexander, R. (2006). Towards Dialogic Teaching: Rethinking Classroom Talk (3 ed.). Thirsk: Dialogos.
Askew, M., Brown, M., Rhodes, V., Johnson, D., & Wiliam, D. (1997). Effective Teachers of Numeracy, Final Report. London: Kings College.
Bakhtin, M. M. (1981). The dialogic imagination: Four essays by M.M. Bakhtin (C. Emerson & M. Holquist, Trans.): University of Texas Press.
Bell. (1993). Principles for the Design of Teaching. Educational Studies in Mathematics, 24(1), 5-34.
Bell, A., Swan, M., Crust, R., & Shannon, A. (1993b). Awareness of Learning, Reflection and Transfer in School Mathematics; Report of ESRC Project R000-23-2329: Shell Centre for Mathematical Education, University of Nottingham.
Bell, A., Swan, M., Onslow, B., Pratt, K., & Purdy, D. (1985). Diagnostic Teaching for Long Term Learning. Report of ESRC Project HR8491/1: Shell Centre for Mathematical Education, University of Nottingham.
Black, P., & Wiliam, D. (1998). Inside the black box : raising standards through classroom assessment. London: King's College London School of Education 1998.
Brousseau, G. (1997). Theory of Didactical Situations in Mathematics (N. Balacheff, M. Cooper, R. Sutherland & V. Warfield, Trans. Vol. 19). Dordrecht: Kluwer.
DfES. (2005). Improving Learning in Mathematics. London: Standards Unit, Teaching and Learning Division.
NCTM. (1988). NCTM Curriculum and Evaluation Standards for School Mathematics: Responses from the Research Community. Journal for Research in Mathematics Education, 19, 338-344.
Stigler, J. W., Gonzales, P., Kawanaka, T., Knoll, S., & Serrano, A. (1999). The TIMSS Videotape Classroom Study: Methods and Findings from an Exploratory Research Project on Eighth-Grade Mathematics Instruction in Germany, Japan, and the United States (NCES 1999-074). Washington, DC: National Center for Education Statistics.
Swan, M. (2005). Improving Learning in Mathematics: Challenges and Strategies. Sheffield: Teaching and Learning Division, Department for Education and Skills Standards Unit.
Swan, M. (2006a). Collaborative Learning in Mathematics: A Challenge to our Beliefs and Practices. London: National Institute for Advanced and Continuing Education (NIACE); National Research and Development Centre for Adult Literacy and Numeracy (NRDC).
Swan, M. (2006b). Learning GCSE mathematics through discussion: What are the effects on students? Journal of Further and Higher Education, 30(3), 229-241.
Swan, M. (2007). The impact of task-based professional development on teachers' practices and beliefs: A design research study. Journal of Mathematics Teacher Education, 10(4-6), 217-237.
Swan, M., & Green, M. (2002). Learning Mathematics through Discussion and Reflection. London: Learning and Skills Development Agency.
Swan, M., & Lacey, P. (2008). Mathematics Matters - An Executive Summary: National Centre for Excellence in Teaching Mathematics.
Vygotsky, L. (1996). Thought and Language (A. Kouzlin, Trans. 9th ed.). Cambridge: Massachusetts Institute of Technology Press.
Watson, A., & Mason, J. (1998). Questions and prompts for mathematical thinking. Derby: Association of Teachers of Mathematics.
Wigley, A. (1994). Models for Mathematics Teaching. In A. Bloomfield & T. Harries (Eds.), Teaching and Learning Mathematics (pp. 22-25). Derby: Association of Teachers of Mathematics.
Appendices: Two further examples of multiple representation tasks
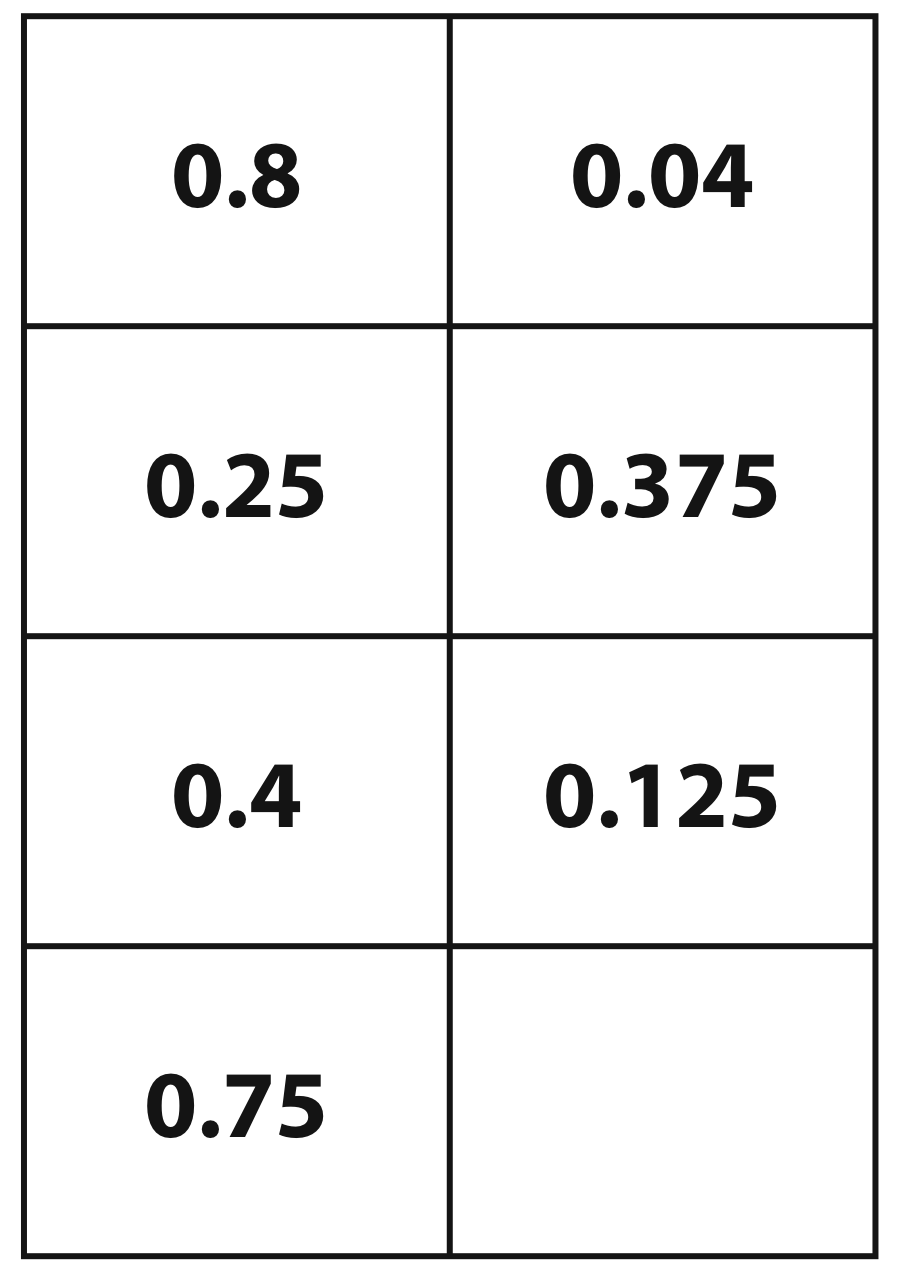
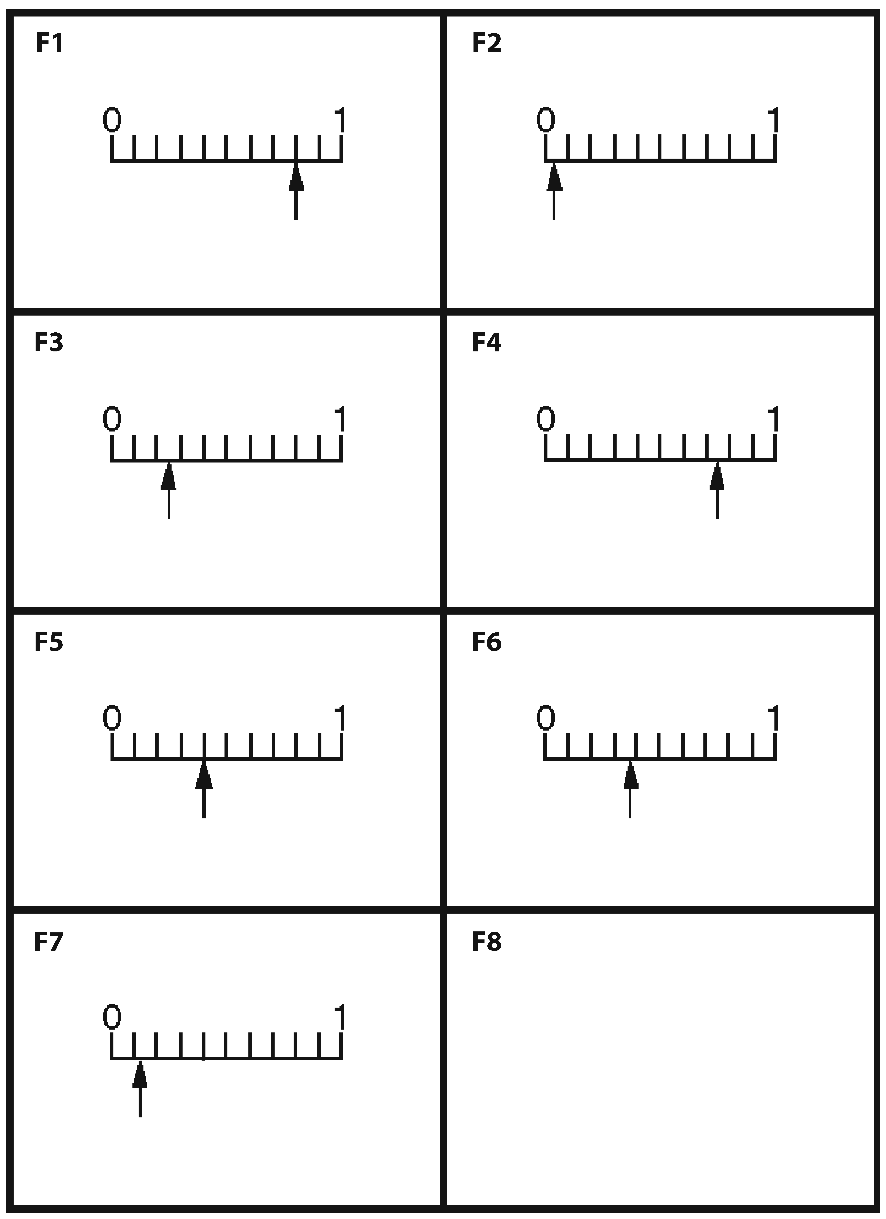
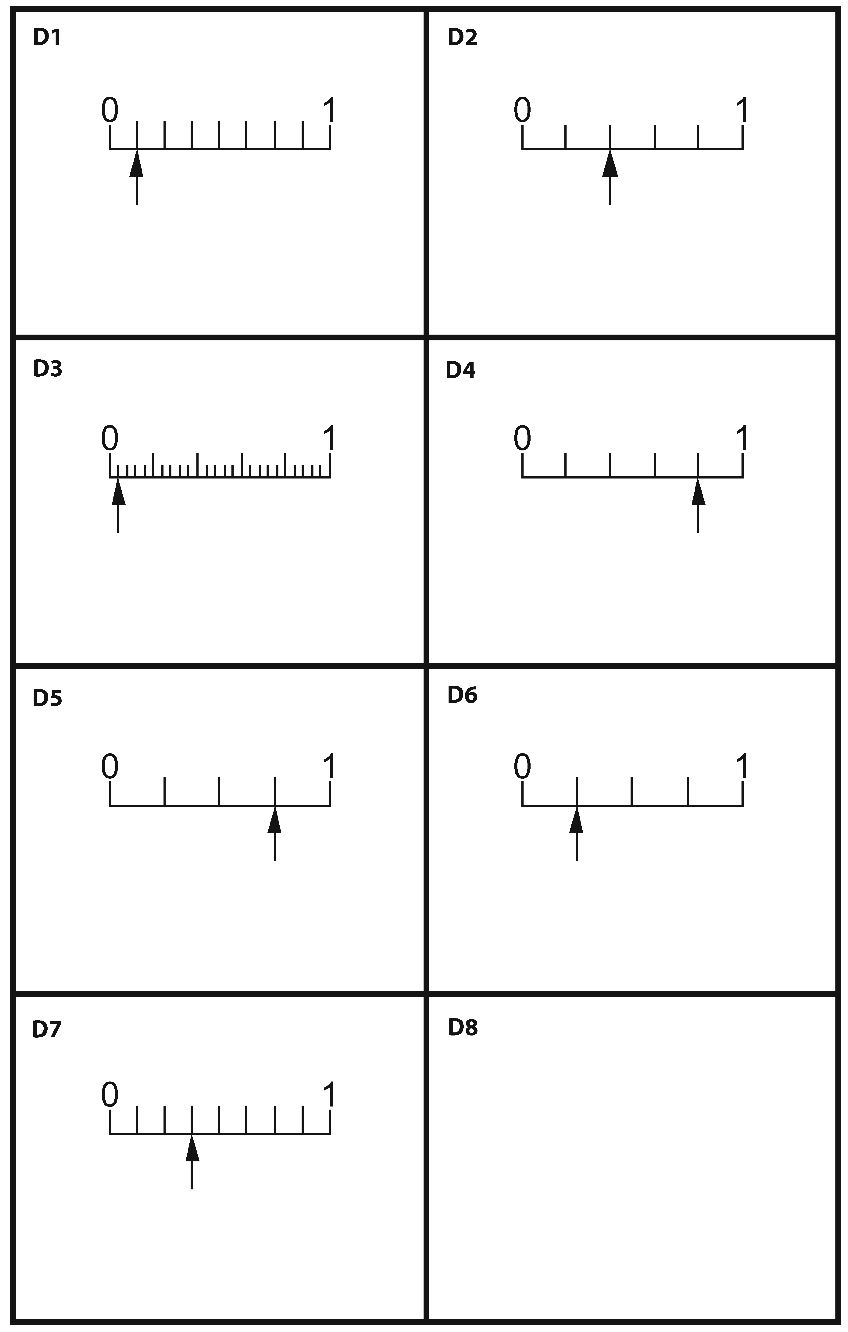
10Example 1: Visualising and ordering decimals and fractions (DfES, 2005)
In this example, students are first asked to order a set of decimals into order of size. This exposes many misconceptions (e.g., size is related to the number of digits). They are then given area and/or number line diagrams to help interpret the numbers. Finally groups of cards are arranged in order of size. The whole process is repeated with the fractions and, over several sessions the six sets are combined.
Decimals 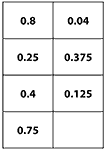 Enlarge Enlarge |
Proportions of a 100 square  Enlarge Enlarge |
Positions on a tenths scale 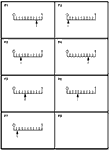 Enlarge Enlarge |
Fractions  Enlarge Enlarge |
Proportions
of a unit square 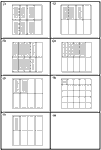 Enlarge Enlarge |
Positions
on assorted scales  Enlarge Enlarge |
Decimals |
Proportions of a 100 square |
Positions on a tenths scale |
|---|---|---|
 |
 |
 |
Fractions |
Proportions of a unit square |
Positions on assorted scales |
 |
 |
 |
Example 2: Frequency graphs, Cumulative frequency graphs, and Box and whisker plots (DfES, 2005)
This is an example of a much more demanding task, where students match frequency graphs, cumulative frequency graphs, and box and whisker plots, for large samples.
Words  Enlarge Enlarge |
Box and whisker plots  Enlarge Enlarge |
Frequency graphs  Enlarge Enlarge |
Cumulative frequency graphs  Enlarge Enlarge |
Words |
Box and whisker plots |
|---|---|
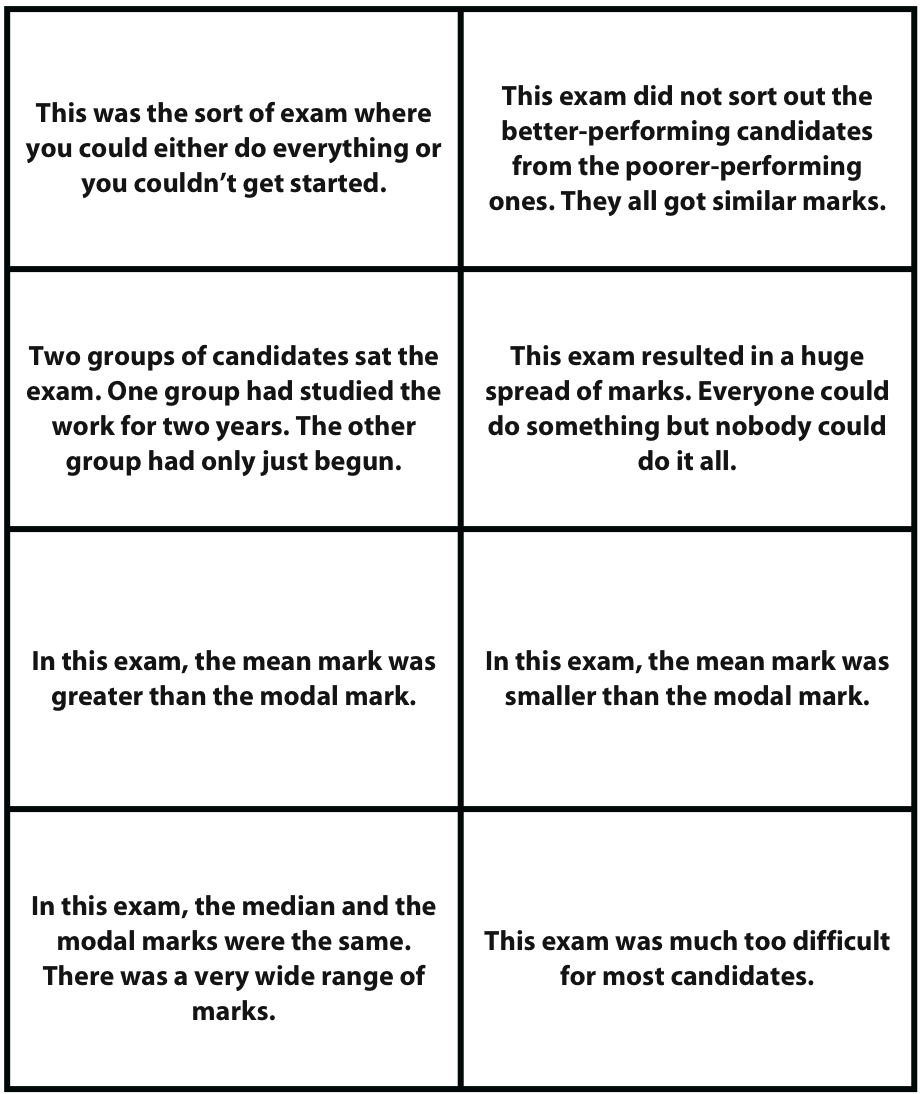 |
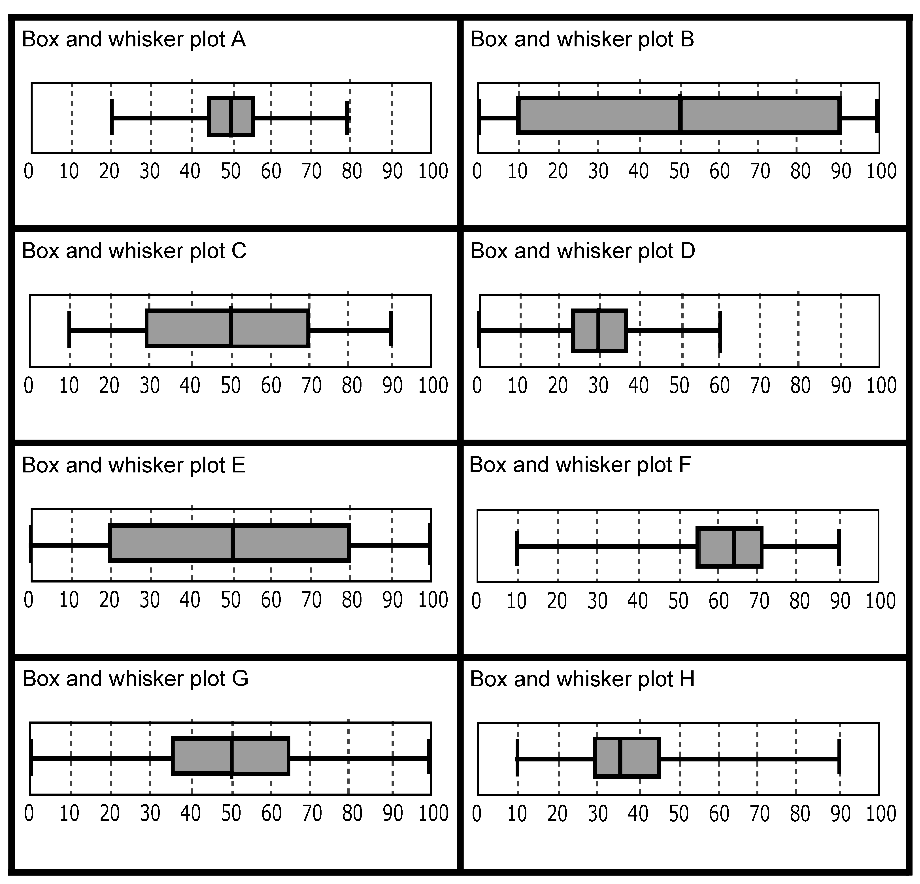 |
Frequency graphs |
Cumulative frequency graphs |
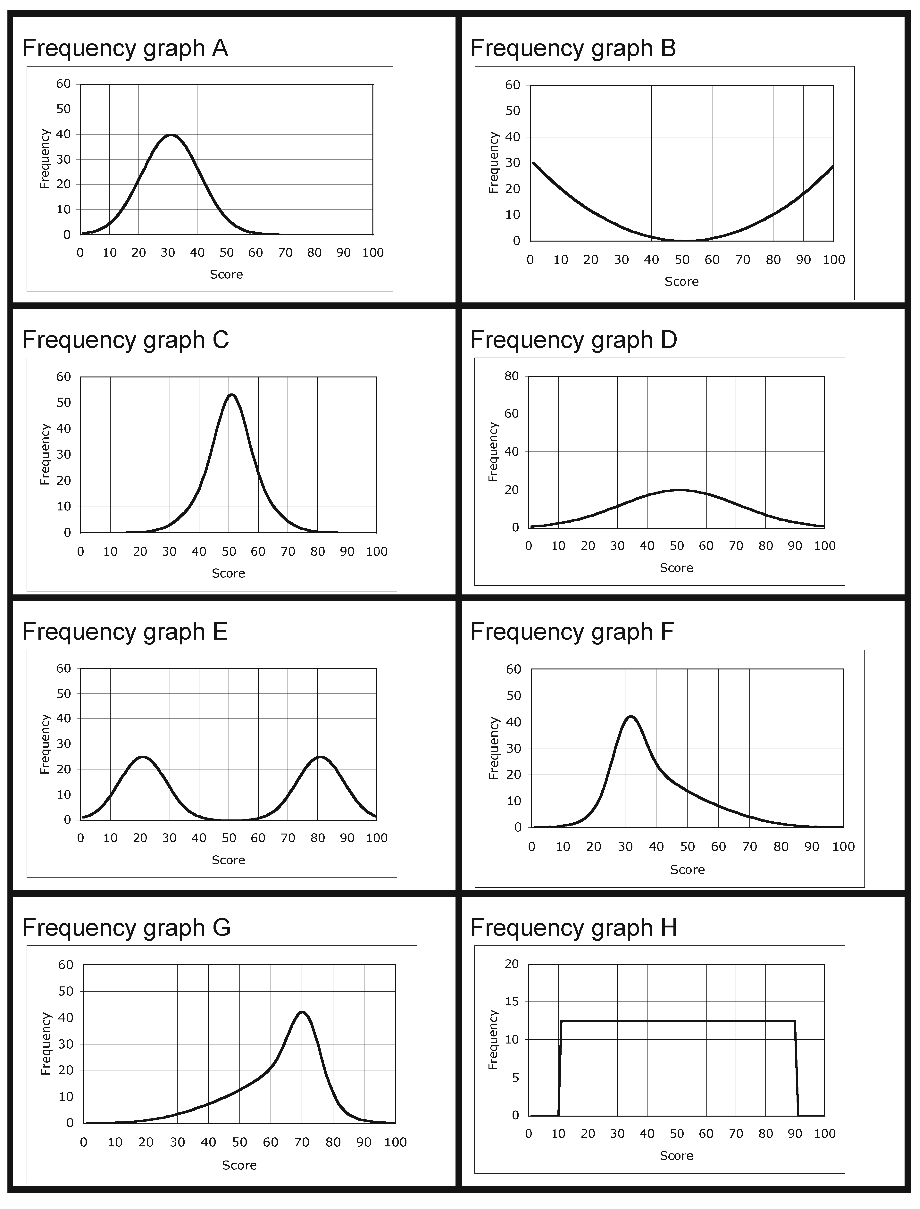 |
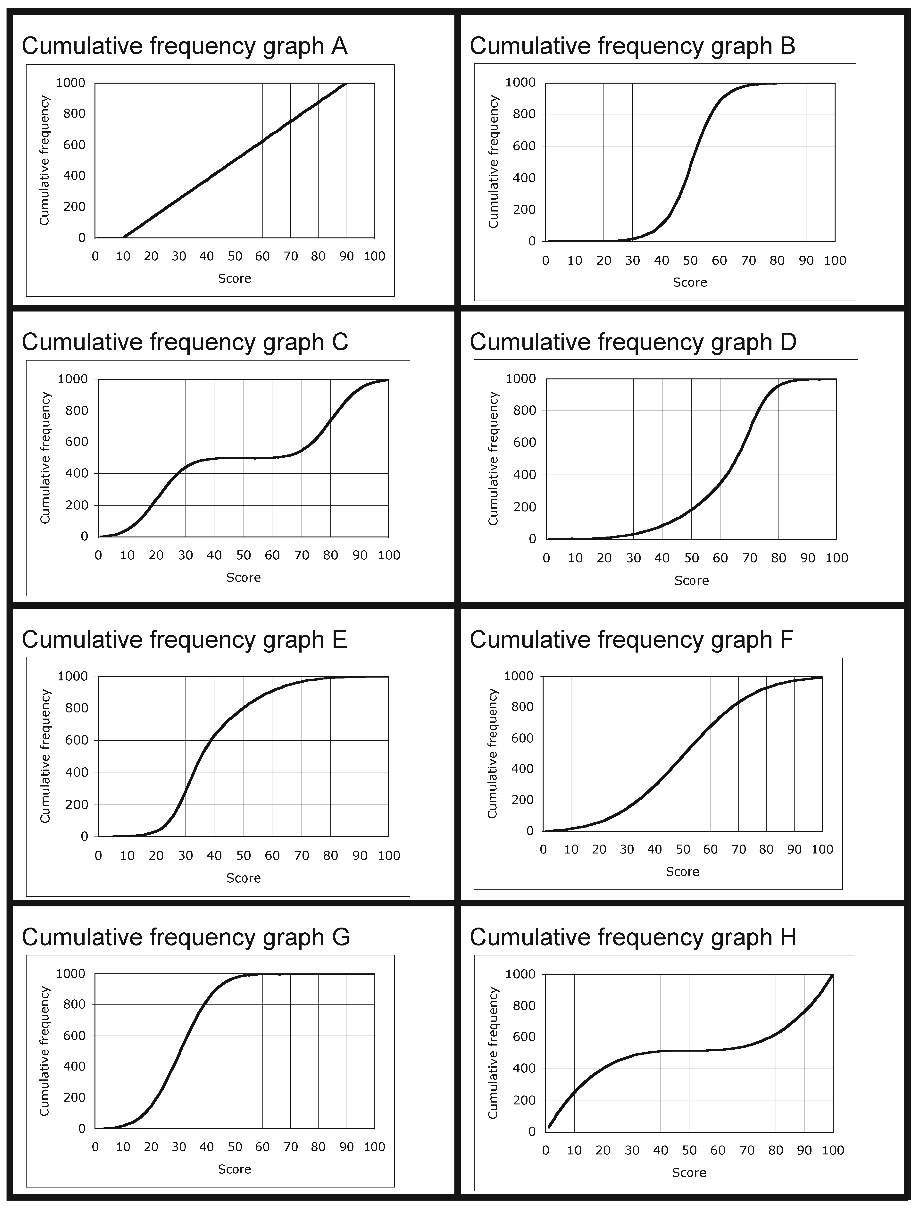 |
About the author
11Malcolm Swan is Associate Professor and Reader in Mathematics Education at the University of Nottingham and has been a leading designer-researcher since he joined the faculty in the Shell Centre for Mathematical Education in 1979. His interests lie in the design of teaching and assessment, particularly the design of situations which foster reflection, discussion and metacognitive activity, the design of situations in which learners are able to construct mathematical concepts, and the design of assessment methods that are balanced across learning goals – and thus have a positive backwash effect on teaching and learning. Diagnostic teaching, using ‘misconceptions’ to promote long term learning, has been an ongoing strand of this work.
He has led design teams on a sequence of internationally funded research and development projects including work for UK examination boards and the US NSF-funded Balanced Assessment project and the Mathematics Assessment Resource Service (MARS). He has designed courses and resources for the professional development of teachers, evaluating their impact on student learning and on the beliefs and practices of experienced teachers. These materials have been sent by the UK Government and the Bowland Trust to all schools and other relevant educational institutions. In 2008 he was awarded the ISDDE Prize for educational design for The Language of Functions and Graphs.