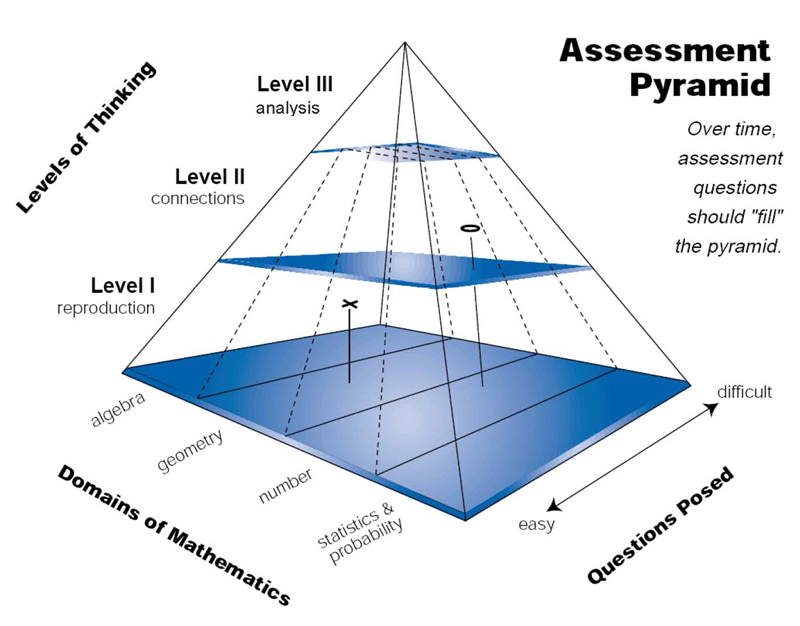
The assessment pyramid was first developed in 1995 by researchers at the Freudenthal Institute to support the design of the Dutch National Option for the Third International Mathematics and Science Study (Dekker, 2007) and later adapted by Shafer and Foster (1997) for use in research studies in the United States (see Figure 1). The relative distribution for the different levels of thinking – reproduction, connections, and analysis – illustrates that even though recall tasks still form the majority of assessment questions asked using this approach, to assess understanding they cannot be the only type of assessment task used with students. Teachers need to move beyond a battery of questions designed to assess student recall and include tasks that allow students to show that they can relate mathematical representations, communicate their reasoning, solve problems, generalize, and mathematize context problems. As part of CATCH, teachers engaged in activities designed to facilitate discernment of tasks used to elicit three types of mathematical reasoning: reproduction, connections and analysis.

Designing Professional Development
for Assessment
David C. Webb
University of Colorado at Boulder
Design considerations for a professional development model that supports teachers’ formative assessment practices
Abstract
1Teachers rarely have opportunities to engage in assessment design even though classroom assessment is fundamental to effective teaching. This article describes a process of design, implementation, reflection and redesign that was used to create a model for professional development to improve teachers’ assessment practices. The improvement of the professional development model occurred over a period of eight years, in two different research projects involving middle grades mathematics teachers in the United States. This article also describes the design principles that teachers used to design classroom assessments and “learning lines” to support formative assessment of student understanding.
Teachers who strive to teach for student understanding need to be able to assess student understanding. There are few opportunities, however, for teachers to develop their conceptions of assessment or to learn how to assess student understanding in ways that inform instruction and support student learning. In working with teachers from across all grade levels, it is clear that there is demand for additional support in classroom assessment and a willingness to admit limited expertise in several key facets of assessment. In fact, in contrast to teachers in other disciplines, there seems to be greater doubt expressed by mathematics teachers about the design of the quizzes and tests they use and the usefulness of those tasks for eliciting student responses that might exemplify student understanding of mathematics. Contrast the typical classroom assessments in mathematics with scientific inquiry promoted in student-initiated experiments in science labs, genre-based writing in language arts, extended conversations in a foreign language class. The comparison is easy to appreciate even without empirical evidence. Teachers’ limited conceptions of and confidence in assessment often restrict implementation of mathematics curricula designed to achieve more ambitious goals for student learning such as non-routine problem solving, modeling, generalization, proof and justification. At present, therefore, there is an urgent need to provide mathematics teachers opportunities to develop their expertise in classroom assessment.
The purpose of this article is to articulate the design process for professional development that aims to improve teacher expertise in the selection, adaptation, and design of assessment tasks, and the instructional decisions informed by their use. To provide a framework for this process, I will briefly outline some of the theoretical assumptions that drive the choices made to develop a learning trajectory for teachers and the related professional development activities. This is followed by a discussion of professional development activities that were developed within the context of the Classroom Assessment as a basis for Teacher CHange (CATCH) project and later used as part of the Boulder Partnership for Excellence in Mathematics Education (BPEME) project. Links to products developed by the BPEME teachers such as assessment tasks, interpretation guides, and maps to support formative assessment decisions, are included to exemplify the necessary interrelationship between assessment and curriculum. This article concludes with reflections about the design of professional development for classroom assessment and recommendations for future work in this area.
Design problem: Professional development for classroom assessment
2The origins of this design problem for professional development emerged as an unexpected result of work with mathematics and science teachers as they were implementing inquiry-oriented curricula in their classrooms. These teachers could be characterized as the restless innovators in their schools who were willing to use drafts of activity sequences with their students, sometimes encompassing four to six weeks of instruction. Our research group, which included faculty and graduate assistants at the University of Wisconsin and researchers from the Freudenthal Institute, had the opportunity to observe math and science teachers as they implemented challenging and thought-provoking material with their students (Romberg, 2004). Afterwards, in a series of semi-structured interviews with these innovative elementary, middle and high school teachers, we found that while they were thrilled at what their students were able to do with the new material, they were quite uncertain about how they could document what their students actually had learned in the form of summative assessments (Webb, Romberg, Burrill, & Ford, 2005). That is, there was a mismatch between the learning and emerging understanding that was evident in student engagement and classroom discourse about the activity and the manner in which teachers assessed what students had learned. Although some of the science teachers later shifted their attention to assessment opportunities that were present within the instructional activities, the mathematics teachers were less inclined to do so. This suggested some discipline-specific issues related to assessment and eventually led to a problematizing of the assumptions they made about assessment and grading (Her and Webb, 2004). Namely, how do teachers who strive to teach for student understanding assess student understanding of mathematics? How do students demonstrate understanding of mathematics and what types of tasks can be used to assess such understanding?
It is worth noting that at the time this design problem emerged, much had already been written in the United States about a new vision for classroom assessment in school mathematics (Lesh & Lamon, 1993; Romberg, 1995), many new mathematics curricula had been published that teachers could used to achieve this vision, and several noteworthy resources were available to support classroom assessment, such as the Mathematics Assessment Resource Service (http://www.nottingham.ac.uk/education/MARS/tasks/ ) and the Balanced Assessment in Mathematics (http://balancedassessment.concord.org/). However, while these materials are necessary to support change in classroom assessment, teachers are unlikely to learn how to use such materials effectively without reflecting on their current assessment practices and re-grounding such practices in principles that help articulate what it means to understand mathematics and how student understanding can be assessed. Professional development that aims to improve teachers’ assessment practices, therefore, needs to consider teachers’ conceptions of assessment and the ways in which their instructional goals might be demonstrated by students. Facilitating change in teachers’ assessment practice is not so much a resource problem as it is a problem of: a) creating opportunities for teachers to reconceptualize their instructional goals, b) re-evaluating the extent to which teachers’ assessment practices support those goals, and c) helping teachers develop a “designers’ eye” for selecting, adapting and designing tasks to assess student understanding.
Classroom Assessment as a Basis for Teacher Change (CATCH[1])
3The CATCH project sought to support middle school mathematics teachers’ assessment of student understanding through summer institutes and bi-monthly school meetings over a period of two years. As summarized by Dekker and Feijs (2006), “CATCH was meant to develop, apply and scale up a professional development program designed to bring about fundamental changes in teachers’ instruction by helping them change their formative assessment practices” (p. 237). The effort to “scale up” forced the project team to focus on a well-articulated model for assessing student understanding that would be relevant to a large number of mathematics teachers across various grade levels and school contexts, and so we decided to centralize our professional development around the Dutch assessment pyramid. This model and the project’s hypothetical professional development trajectory for assessment are outlined here as initial design principles that were reexamined and revised later for the BPEME project.
The Dutch Assessment Pyramid
(from Shafer & Foster, 1997, p. 3).
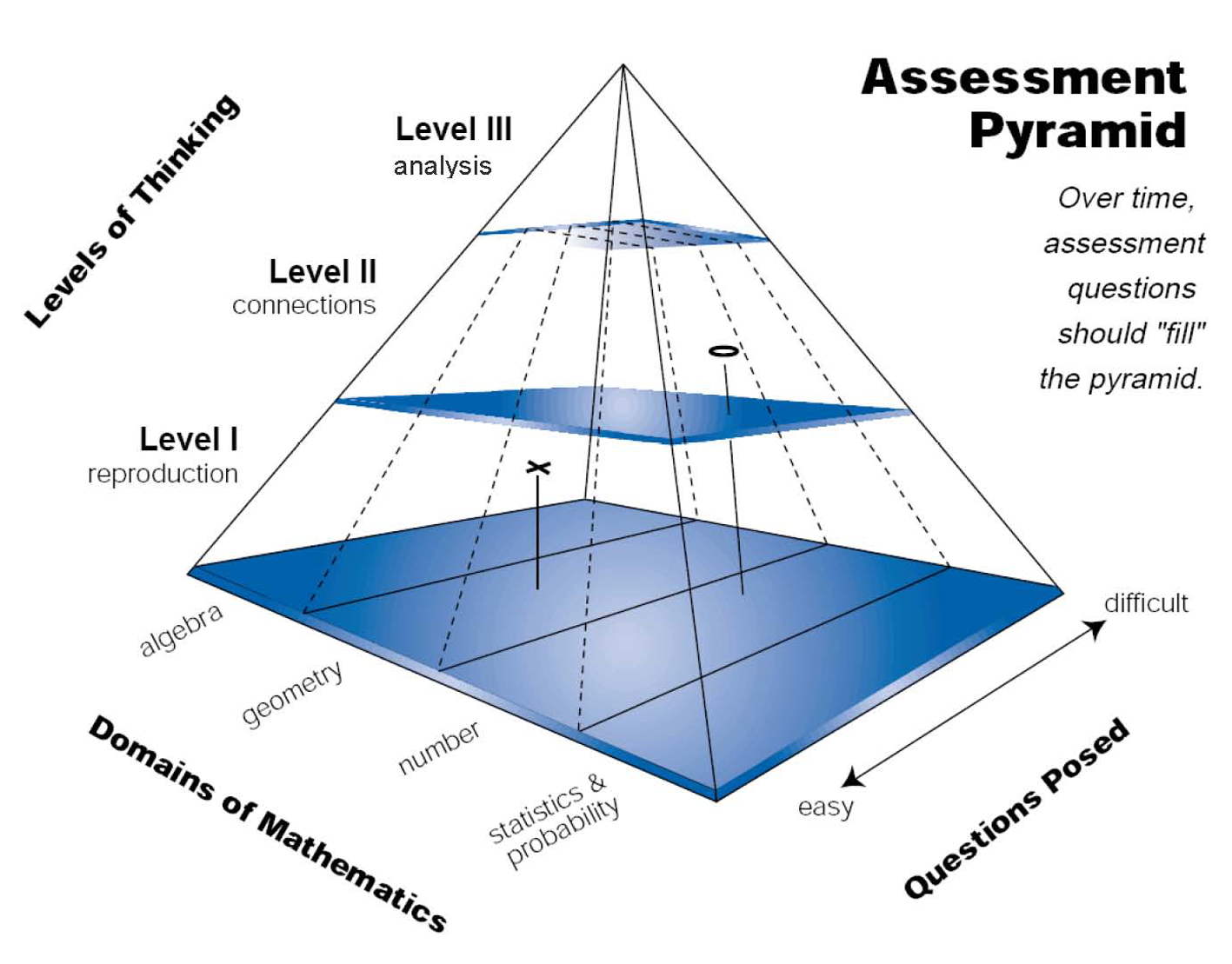
- Reproduction:
- The thinking at this level essentially involves reproduction, or recall, of practiced knowledge and skills. This level deals with knowing facts, recalling mathematical objects and properties, performing routine procedures, applying standard algorithms, and operating with statements and expressions containing symbols and formulas in “standard” form. These tasks are familiar to teachers, as they are found in the most commonly used tasks on standardized assessments and classroom summative tests, and tend to be the types of tasks teachers have an easier time creating on their own analysis.
- Connections:
- The reasoning at this level can involve connections within and between the different domains in mathematics. Students at this level are also expected to handle different representations according to situation and purpose, and they need to be able to distinguish and relate a variety of statements (e.g. definitions, claims, examples, conditioned assertions, proofs). Items at this level are often placed within a context and engage students in strategic mathematical decisions, where they might need to choose from various strategies and mathematical tools to solve simple problems. Therefore, these tasks tend to be more open to a range of representations and solutions.
- Analysis:
- At this level, students are asked to mathematize situations—that is, to recognize and extract the mathematics embedded in the situation and use mathematics to solve the problem, and to analyze, interpret, develop models and strategies, and make mathematical arguments, proofs, and generalizations. Problems at this level reveal students’ abilities to plan solution strategies and implement them in less familiar problem settings that may contain more elements than those in the connections cluster. Level III problems may also involve some ambiguity in their openness, requiring students to make assumptions that “bound” an open problem so that it may be solved.
It is also important to note another dimension illustrated by this pyramid – difficulty. That is, tasks at Level II and III are not necessarily more difficult than tasks from the reproduction level, although they often can be. To the contrary, some students who find Level I tasks difficult may be more successful in solving Level II or III problems, a phenomenon that was observed on several occasions by CATCH teachers.
Tasks from the Assessment Pyramid
Another feature of task design that is not articulated in the assessment pyramid, but seems to parallel the levels of thinking dimension, is task format. Tasks that are designed to elicit student recall generally appear in formats that are commonly found on large scale standardized assessments: multiple choice, short answer, matching, etc. As it turns out, these task formats also happen to be what many teachers use on their summative assessments, since they are easy to find and easy to score. Figure 2 is a representative example of a teachers’ summative assessment, collected prior to participating in professional development.
Also consider the student responses elicited from this assessment. In almost all cases, the answers are correct or incorrect with little opportunity for students to demonstrate partial understanding. While this eases the grading demands for the teacher, such responses limit the opportunities for teachers to offer feedback that relate students’ errors to potential misconceptions. At best, feedback in this case is directed toward “you either get it or you don’t” (Otero, 2006). Even though these types of tasks and the skills they assess are a necessary part of assessing student understanding (as suggested by the base of the pyramid), the possibilities for formative assessment are limited to practice and recall cycles. For teachers who strive to improve formative assessment, they find that offering substantive feedback to student responses to Level I tasks is a real challenge, motivating the need to use tasks that assess Level II and III reasoning. One exception to this can be accomplished by selecting a cluster of Level I tasks to address slightly different aspects of a related strategy or concept. With a cluster of tasks, instead of evaluating student work for each task, teachers can infer elements of student understanding and offer feedback based on a holistic, qualitative judgment of student work and strategy use across tasks.
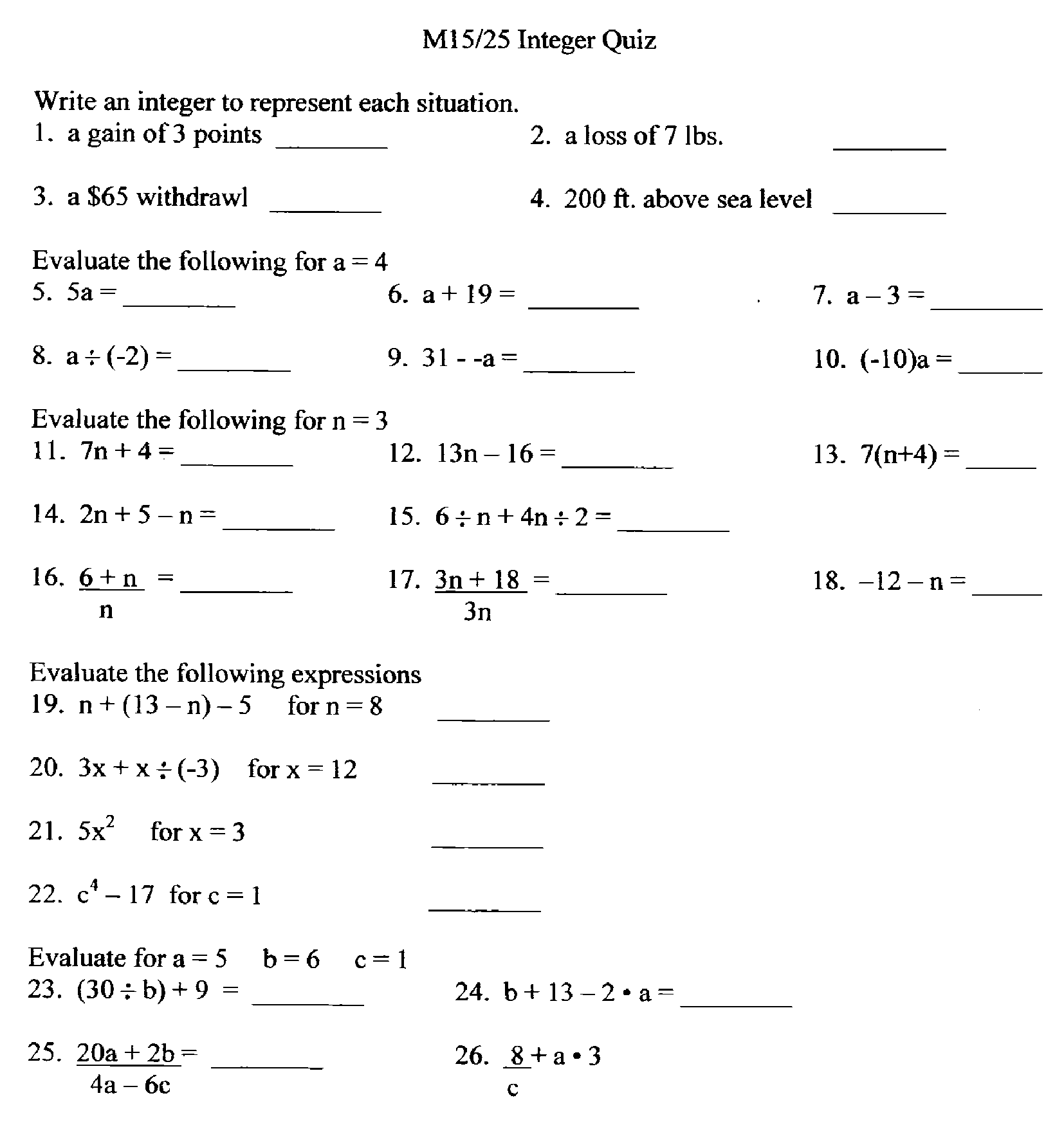
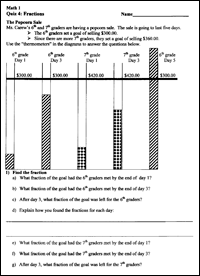
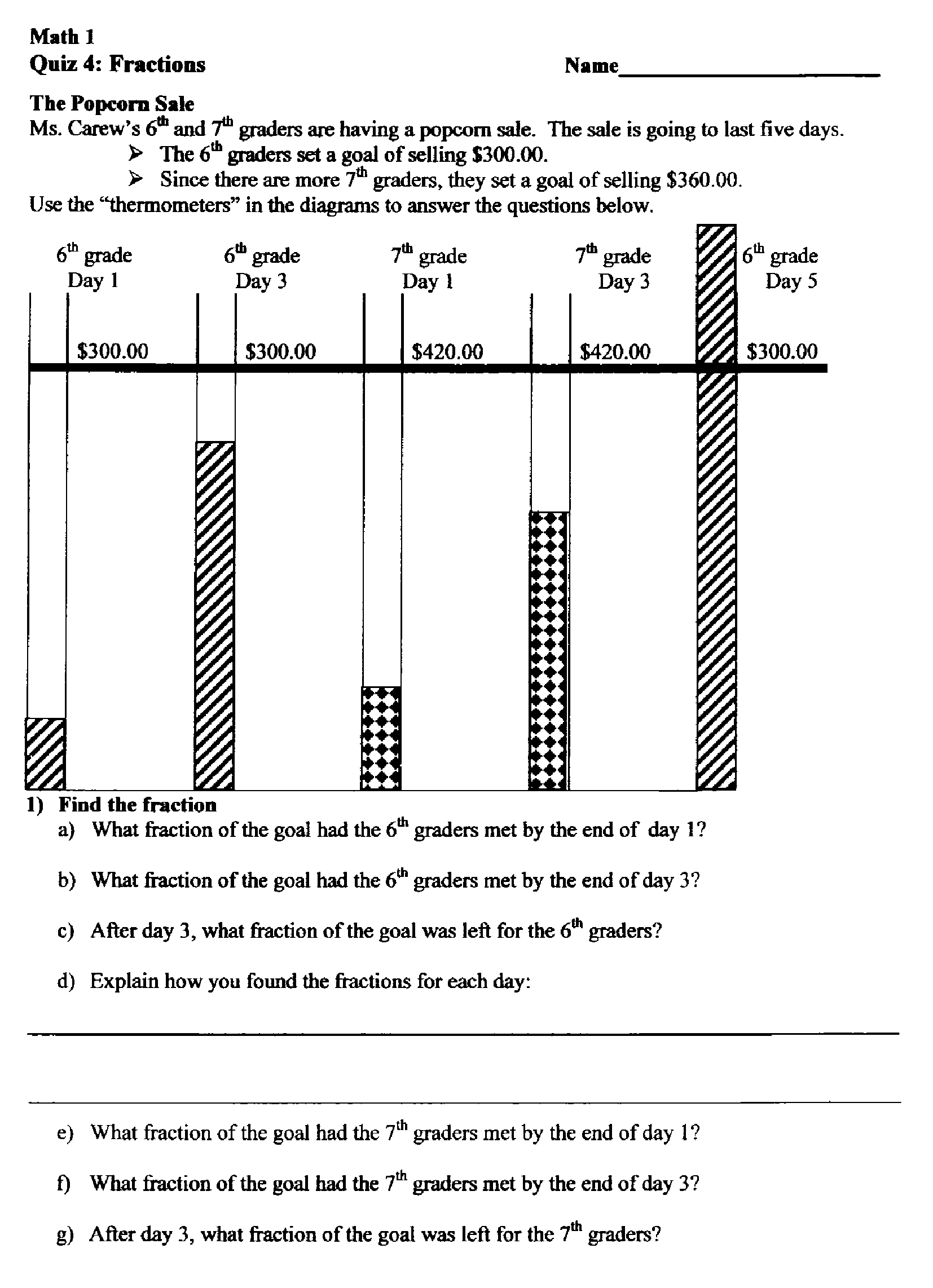
Level II tasks involve formats that are necessarily more open. They usually require students to construct responses rather than select responses. In some cases, a higher level task requires students to select between two or more options, however the emphasis is on how students justify their choice rather than what they choose. The “openness” of Level II problems to a range of student representations and solution strategies provides teachers much more information about students’ strategic competence, reasoning, mathematical communication, and their ability to apply skills and knowledge in new problem contexts. Figures 3 through 5 are a sample of Level II tasks designed by teachers participating in the CATCH and BPEME projects.
Figure 3 includes a set of fraction bars (with no measurement guides) that represent the amount of money collected for a school fundraiser. To find the different fractions that represent the shaded information, students need to choose from several different visually-oriented strategies or estimate (which, in this case, is not the teachers’ preferred strategy).
For example, to figure out the fractional amount shaded in the first thermometer students can continue to mark the measures for halves, fourths, and eights (by folding), use the shaded part to mark equal portions moving up the thermometer, or perhaps even use a ruler (there is no indication that this is not allowed). Part d also suggests that both the solution method and the answer are important. In addition to students’ explanations, the teacher could also look at the markings students make on each thermometer to deduce the strategy students use.
The problem in Figure 4 takes a direct approach to assess student understanding of what fractions represent. Students are prompted to describe a situation in which such a fraction might be used. For the given context they describe, students then explain what the numerator and denominator represent. Given students’ familiarity with fractions, this would be an easy Level II problem.
In the Choose and Defend problem (Figure 5), Justin and Jen offer different answers for simplifying an algebraic expression. Jen’s answer is a common error. The potential for eliciting Level II reasoning (i.e., justification) is in the second part of the question. Students can use several approaches (e.g. area model, substitute values, formal example of the distributive property) to defend their choice or to provide a counterexample for the incorrect choice.
In contrast to the Level I questions, student responses elicited from Level II tasks usually involve either short essay responses or a range of appropriate strategies and representations for the same task. Teachers need to interpret more than whether or not the answer is correct and, in many cases, the answer is often secondary to the student’s justification for his or her answer. This places greater demands on teacher interpretation of student work as it opens up a larger window of student reasoning that is more nuanced and complex. Depending on the type of task used, students’ responses may reveal: 1) their belief in a common misconception (e.g. that taking a 25% discount twice means the sale item should be half price), 2) understanding of a fundamental concept even though they cannot perform a related algorithm (e.g. demonstrating a sound understanding of division but confused about how to use the long division algorithm), 3) an ability to communicate their mathematical reasoning, and 4) that they can “see” the mathematical principles in an unfamiliar problem context. These responses generate new possibilities for feedback, for the student about his or her performance in relationship to the instructional goals, and for the teacher with respect to what students are learning from instruction. In a sense, when Level II and III tasks are added to the assessment plan, there is an increase in the quality of evidence that can be used to inform instruction and guide learning. With respect to formative assessment, Level II and III tasks also are more apt to extend the cycle length for formative assessment (Wiliam, 2007, p. 1064), allowing teachers to monitor students’ progress of process skills that cut across units and provide feedback that students will have an opportunity to take in to account in future revisions of arguments and justifications and the next version of an extended written response or project.
For teachers who strive to improve formative assessment, there is a challenge in providing feedback simply due to the sheer quantity of evidence available. As teachers become more familiar with student responses to Level II tasks, they find that the range is finite and often predictable. To support their interpretation of student responses, teachers also learn the importance of articulating how the assessment tasks relate to instructional goals, which can either cut across an entire course or are specific to a particular chapter or unit. As suggested in most current definitions of formative assessment, to offer feedback one needs to know the goals one is trying to achieve.
Since one of the signature features of Level II reasoning is “choosing an appropriate solution strategy or tool,” these tasks need to be more accessible to a range of approaches. To design tasks that are intentionally open to a range of strategies requires a deeper understanding of content and a broader awareness of different ways students solve problems. If teachers have not used instructional materials that are accessible to a range of strategies, or have used primarily Level I assessment tasks that do not elicit a range of strategies, this also creates a professional development challenge (which is addressed later in the discussion of the BPEME project).


Level III tasks, similar to Level II tasks, are also open-ended. They often involve a realistic problem context so that students to have something to “mathematize.” Patterns and situations, however, also serve as a context for generalization and so Level III problems do not always involve real-world phenomena. For example, having students explore features of number and arithmetic (e.g. “Show that if you add two odd numbers, the result is always even”) requires mathematization and generalization of the structure of numbers. As mentioned previously, some tasks categorized at this level are so open that they appear ambiguous, requiring students to set the boundaries by setting the parameters for the problem they are about to solve – in essence, the students are creating problems to solve. Figures 6 through 8b are examples of Level III problems adapted and designed by teachers in the BPEME project.
Figure 6 is a three-part problem that requires students to develop a formula for a rectangle using the area formula for a square. Part c is designed to assess student analysis of the formula they created in part b. Even though a student response requires limited written justification, the process of finding critical values is not something that is addressed in this class: this problem requires students to extend their reasoning to mathematical terrain that they have yet to explore.
Figure 7 is a task designed by a teacher for a unit test for fractions. Students need to recognize the commonalities and differences between the procedures for two operations that students often confuse with one another. Since the procedure of multiplying numerators and denominators when multiplying fractions often misleads students to add numerators and denominators when adding fractions, this task encourages students to make these differences explicit. The expected student response is a written description of the differences between these two operations, with possibly examples of the two fraction operations with labels.
A square has sides of length x centimeters. A new rectangle is created by increasing one dimension by 6 centimeters and decreasing the other dimension by 4.
- Make a sketch to show how the square is transformed into the new rectangle.
- Write an expression for the area of the original square and an expression for the area of the new rectangle.
- For what values of x is the area of the new rectangle greater than the area of the square?
For what values is the area of the new rectangle less than the area of the square? For what values are the areas equal?
The project task (Figures 8a & 8b) is an example of an open-ended assessment that requires an extended duration for student completion. This type of Level III task can include opportunities for teachers to provide feedback to students on progress as they complete the project. In fact, teachers will often choose to include regular checkpoints at different phases of the project to reconcile any differences between student work and the intended goals, giving the student opportunities to respond to the feedback and make necessary revisions.
Another common type of Level III problem designed by teachers is having students design their own problem. The reason this type of problem is categorized as Level III is that it requires students to understand the mathematical focus of the task and options for contexts that can address the mathematics. Students can, of course, draw upon recent experiences in class and recall of specific tasks for the selected topic. But more often than not, teachers have noticed that students choose to be more creative and will select contexts that are not directly drawn from their class activities.
The main challenges teachers cite when they are reluctant to incorporate Level III tasks in their assessments are: a) such tasks require greater demand on student and teacher time, b) these tasks are more difficult to design, and c) the teachers’ perception that it is unfair to ask students to complete tasks that are either ambiguous or unfamiliar on a summative assessment. The additional time students need for reflection and analysis in the generalization examples will infringe upon the time allotted to complete an assessment. To include projects in the menu of assessment formats, teachers need to consider the time it will take for students to complete the project outside of class, the time needed to provide individualized feedback, and the time needed to grade the projects. In spite of the demands on teachers’ busy schedules, some teachers continue to use projects because they address important instructional goals that are difficult to address on quizzes and tests, and they provide opportunities for student ownership, creativity, and application of mathematics.

Teachers often mentioned that while they were confident in their ability to design Level II tasks, the selection and design of Level III tasks was often elusive. Our response to this was heartfelt agreement! Knowing how to craft open-ended problems that had both a perceptible anchor for mathematization and a level of ambiguity that required assumptions to be made, is a challenge for designers with decades of experience. Even after conveying this reality to teachers they still were willing to take up the challenge of identifying Level III problems that appeared in their instructional materials and assessment resources. In fact, given the elusive nature of tasks that elicited Level III reasoning, participants expressed genuine respect when another design team was able to design a Level III task. To summarize, the design challenge for Level III problems should not be understated. Rather, the challenge needs to be explicitly discussed among teachers so that they can gain confidence in their emerging ability when they are able to identify and create their own Level III tasks.
The fairness issue is a genuine source of concern for many mathematics teachers. Quite often, the source of tasks for summative assessments are the problem sets teachers use for homework and class work. The problem with this particular concern is that it suggests that students should not have experiences with Level II and III questions apart from summative assessment. Quite the contrary! Students experiences with the full range of assessment tasks should occur as part of instruction and in various informal assessment contexts. To ease teacher concerns about fairness, we repeatedly encouraged them to use these tasks in low stakes, non-graded situations so they could focus on listening to students’ reasoning and observe different solution strategies. Whether for summative or formative purposes, the significance of using such tasks with students is that they create learning opportunities for students: to make connections, communicate their insights, and develop a greater understanding of mathematics.
Using the assessment pyramid: Key professional development activities from CATCH
To design activities for the CATCH project, we worked under the assumption that assessing student understanding was an implicit goal of participating teachers, even though they may not have yet understood how to operationalize this goal in their classroom practice. We also knew that some teachers might not see a need for change in practice. To motivate teachers to include tasks that assessed more than recall, we knew that we needed to design experiences in which they engaged in these tasks so that they could appreciate first-hand what Level II and III reasoning involved. Of course, it is one thing to expect teachers to solve Level II/III problems. The next challenge is that once teachers understood the reasoning elicited by such tasks, and the format and design principles related to Level II/III tasks, how could we convince teachers to use such tasks with their students? The core sequence of professional development activities for the assessment pyramid was therefore designed to address the following essential questions: What is classroom assessment? How is student understanding assessed? To what extent do our current practices assess student understanding? What are some ways to assess student understanding in mathematics that are practical and feasible?
What is classroom assessment? Unfortunately, teachers often develop a set of classroom assessment routines with little opportunity to examine and reflect on their concepts of classroom assessment and how this informs their decisions about the selection and design of questions and tasks, how they interpret student responses, and how to respond to students through instruction and feedback. As an introductory activity, to promote open communication among participants and provide the facilitators an informal assessment of teachers’ conceptions about assessment, we begin with a teacher reflection, sharing, and open discussion of the following questions:
- What is your definition of assessment?
- Why do you assess your students? How often?
- What type of assessments do you use to assess your students?
After several teachers have had an opportunity to share their opinions and common practices, the facilitators orient the discussion to articulate a broader view of classroom assessment, one that involves the familiar summative forms but also includes informal, non-graded assessment such as observing and listening to students engaged in class activities, listening to students' responses during instruction, noting differences in student engagement, and so on. Because several of the CATCH activities are focused on the design of written assessments, it is important to situate that work in the context of a broader and more complete conception of classroom assessment. Before teachers transition to the assessment pyramid activity, there is general agreement among the teachers that the purpose of formal assessment is mostly used to justify grades, and the goal of informal assessment is to identify the strengths and needs of students. This also leads to a discussion of the differences in purpose between formative and summative assessment, and the notion that both of these purposes can be addressed with formal assessment techniques.
Since the initial emphasis of CATCH and the Assessment Pyramid is on task design, we had to give careful attention to how this design work could help teachers understand how formative assessment can be used to inform instruction and promote student learning. As described by Black et al. (2003), assessment is formative when “it provides information to be used as feedback by teachers, and by their students in assessing themselves and each other, to modify the teaching and learning activities in which they are engaged,” (p. 2). We argued, however, that to inform instruction, teachers must be cognizant of methods and tools to assess students’ prior knowledge, skills, and understanding.
Since formative assessment has been used to justify everything from district policy directives (such as quarterly benchmark assessments) to handheld response devices for students (e.g. “clickers”), it is important to reconcile the rhetorical noise that is present in educational sales literature and district-sponsored inservices. Teachers need space to articulate their conceptions of formative assessment and the related instructional decisions they can expect to observe or experience. Later, the shared vision for formative assessment is revisited in practical explorations such as: What types of tasks are more likely to support formative assessment that informs instruction? Which tasks are more likely to create opportunities for more substantive feedback about concepts or procedures, and which tasks are more likely to focus on feedback limited to whether the answer is correct or not? And through examination of classroom video, what are examples of instances in which teachers are responsive to students’ responses?
The Leveling Activity. Before teachers are able to critique their own assessments they need to develop their interpretive skills to identify the reasoning elicited by different assessment tasks and be able to justify those choices. To prepare for the activity we collect various tasks from teacher resources, instructional materials, and standardized tests that exemplify the various levels of thinking. We also make sure to select some tasks that are designed by the teachers. As we sort through the tasks to select a sample to use with teachers, we make notes of our own reasons for classifying tasks at a particular level.
After reviewing principles for classroom assessment, and the need to assess more than recall, we present the assessment pyramid as an ideal distribution model for the tasks that should be used to promote and assess understanding. Definitions for each level are presented along with multiple exemplar tasks. It is also important to highlight the difference between difficulty and reasoning; they are, in fact, two different dimensions in the pyramid. After the overview, teachers are asked to complete several tasks that represent each of the reasoning levels and are reminded to reflect on their thought processes as they solve each problem. Next, they break into small groups to discuss the assessment tasks and classify the potential level of reasoning elicited. An important issue to discuss is that the level of reasoning elicited also depends on the instruction that preceded the task. For example, through additional instructional emphasis students can be taught how to set up and solve particular types of application problems, to the point where the reasoning required to solve the problem is reduced to recall. Teachers’ familiarity with problems that are common to a particular grade level or course should be brought to bear when classifying tasks.
As a follow-up to the leveling activity when teachers were asked to examine their own assessments with respect to the levels of thinking, teachers found that they rarely used assessment tasks designed to elicit a range of student strategies or evidence of student understanding. Teachers concluded they were not giving students opportunities to gain ownership of the mathematical content and were only asking students to reproduce what they had been practicing. Just as important, this motivated teachers to adapt their assessment practices to address more than student recall of skills and procedures. In situations in which teachers submitted a sample of their assessments in advance, we would select and discuss a small sample of tasks to demonstrate ways in which some colleagues were already utilizing Level II and III tasks. In the BPEME project, we noticed one teacher who regularly included a set of problems called “You Be the Teacher,” which included mathematics procedures with common errors that students needed to identify and correct. We regarded this type of error correction as Level II reasoning. Given teachers' familiarity with common student errors, this type of task and several other variations became a popular way to include Level II tasks in units that had a strong emphasis on procedures.
Assessment Design Experiments. Even though the Leveling Activity enhances teachers’ awareness of different features of assessment design, teachers are reluctant to incorporate Level II and III tasks into their regular assessment practices unless they have more compelling evidence that their students will benefit and be able to respond. They perceive the higher level tasks as more difficult, even though they may be easier for some students than the tasks requiring memorization and recall.
To encourage further teacher exploration into classroom assessment, we asked teachers to choose one aspect of classroom assessment that they would “experiment” with over the course of a school year. Since these choices drew from teachers’ prior experiences with, and conceptions of assessment, the assessment experiments were wide-ranging and idiosyncratic, similar to the teacher assessment explorations described in the King’s-Medway-Oxfordshire Formative Assessment Project (Black et al, 2003). One veteran teacher of 35 years chose to make greater use of problem contexts on her assessments. A high school mathematics teacher worked with a colleague to design and use at least one Level II or III task on each quiz or test in each class. One middle grades teacher incorporated more peer and self-assessment activities, while another designed and used more extended projects with her students. Even though, on the surface, many of the teacher experiments appeared to focus on formal, summative assessment practices, these changes in practice were often enough of a catalyst to encourage teachers to examine their instructional goals, interaction between teacher and students, and the need to collaborate in assessment design.
CATCH: Impact on teachers’ conceptions and practices
Over a period of two years, CATCH teachers completed a 4-day workshop with the CATCH design team, led bi-monthly meetings with fellow teachers, and co-facilitated two 4-day summer workshops. Teacher interviews, classroom observations and analysis of assessments used with students, collected at the beginning, middle, and conclusion of the CATCH project, revealed a broadening of teacher conceptions of classroom assessment, greater attention to problem contexts, greater use of Level II tasks, and a reduction in the quantity of tasks on summative assessments (Dekker & Feijs, 2006). Furthermore, as teachers adapted practices, they began to rethink the learning objectives of their curricula and the questions they used during instructional activities. Considering that most professional development sessions focused on the design of written tasks, the dissemination of CATCH design principles into teachers’ instructionally embedded assessment, in retrospect, was an unexpected but logical result.
Even though results from CATCH demonstrated change in teacher practice, we were not satisfied with the degree to which teachers designed new problems or their success in adapting problems to address broader reasoning goals. The most frequently observed change in practice was teacher selection of tasks to assess more than recall. To some extent, teacher adaptation and design of assessment tasks was limited by the instructional resources they used (i.e., teachers who used instructional materials that included few examples of Level II and III tasks had fewer examples to draw from). When we considered why some teachers were more successful than others with assessment design, we assumed that greater teacher engagement in the design process would require professional development that gives greater attention to teachers’ conceptions of how students learn mathematics in addition to teachers’ conceptions of assessment.
CATCH in retrospect: A professional development trajectory for assessment
After reflecting on the nature of professional development activities that characterized the CATCH project, we found that the organic, teacher-centered design process involving reiterative planning of “what should we do with teachers next,” played out as an implicit trajectory for teacher learning that we identified as four categories: initiate, investigate, interpret, and integrate (Figure 9).

Although these clusters are described as a trajectory for teacher activities, the development of teachers’ conceptions and expertise in assessment is not as predictable as a trajectory would imply. The collective beliefs and interests of participating teachers must be considered when designing specific professional development activities for these clusters.
- Initiate.
- Professional development activities in this category were designed to initiate and motivate teacher learning through critique of current practices and prior experiences with classroom assessment. Teachers’ current practice is used as a starting point for professional development as teachers examine, share, and discuss their conceptions of classroom assessment. Teachers completed assessment activities (as if they were students) and reviewed various assessments designed to exemplify the purpose and use of different formats. Expected teacher outcomes of the initiate phase were: reflection on the pros and cons of current assessment methods, and consideration of a goal-driven approach to assessment design that involves more than Level I tasks.
- Investigate.
- Professional development activities in this category were designed to engage teachers in the investigation, selection, and design of principled assessment practices. Using the levels of reasoning in the assessment pyramid, teachers developed practical expertise in selecting assessment tasks. Teachers were encouraged to select, adapt and design tasks to assess student understanding. Expected teacher outcomes of the investigate phase included teacher classification of tasks, greater classroom use of tasks from the connections and analysis levels, and use of other assessment formats (e.g. two-stage tasks, projects, writing prompts).
- Interpret.
- Professional development activities in this category supported teachers’ principled interpretation of student work. In general, when teachers had an opportunity to analyze students’ responses to problems from the connections and reflection levels, they gained a greater appreciation for the value of such tasks. Expected outcomes of the interpret phase included teachers’ improved ability to recognize different solution strategies and teachers using student representations to inform instruction.
- Integrate.
- Professional development activities in this category were designed to support teachers’ principled instructional assessment. Video selections of classroom practice (e.g. Bolster, 2001; Annenburg Media, 2009) were used to broaden teachers’ awareness of assessment opportunities and discuss how teachers used instructionally embedded assessment to guide instruction. Teachers discussed ways to assign a greater share of the assessment process to students, through use of peer and student self-assessment. The expected outcomes of the integrate phase were greater understanding of how assessment informs instruction, teacher experimentation with ways to use student written and verbal thinking to inform instruction, and greater responsiveness to students during instruction.
This trajectory is therefore a meta-level summary of CATCH activities over the course of the project that combined our expectations for teacher learning and observations of teacher change as witnessed in CATCH and other assessment-related projects (Romberg, 2004; Webb et al, 2005). This meta-analysis of project activities was motivated by our interest in continuing this work with CATCH teachers and our need to develop a generalized blueprint that could be used to respond to professional development requests we received from other school districts. Unfortunately, we were not able to secure funding for the continuation of CATCH and so we had to shift our attention to other projects. Several years later, however, we had the opportunity to revisit the elements of this trajectory and combine assessment design with learning progressions for mathematics content in the Boulder Partnership for Excellence in Mathematics Education (BPEME) project.
Teacher Change in Classroom Assessment Revisited – The BPEME Project
4The BPEME project was a three-year professional development program involving 32 middle grades math teachers from seven middle schools in the Boulder Valley School District (BVSD). The design team included BVSD math coaches, applied math and education faculty from the University of Colorado at Boulder, and researchers from the Freudenthal Institute. The design framework we used to select and sequence BPEME activities integrated the previously described assessment design trajectory and the sustained exploration of the development of student skills and reasoning within three essential content areas for middle grades mathematics in the United States: operations with rational numbers, proportional reasoning, and algebraic reasoning. In addition to the assessment and content objectives for teacher learning, the underlying goal of BPEME was to support classroom assessment practices that would be more likely to increase student access to mathematics to reduce the achievement gap between different student demographic groups. This goal was explicitly requested by the funding agency, the Colorado Department of Education, in their solicitation for grant proposals and was certainly a result we hoped would emerge from such work as well. In contrast to CATCH however, rather than considering student achievement as an implicit rationale for improving teachers’ classroom assessment practices – as suggested in Black and Wiliam’s (1998) well-known meta-analysis of research in classroom assessment – the collective effort to “close the achievement gap” was a goal that was explicitly and repeatedly emphasized in BPEME sessions. This achievement orientation influenced the work of the design team in the selection and discussion of activities, and in the evaluation of project results; this orientation also influenced teachers’ motives and their sustained participation in BPEME.
BPEME: An iterative model for professional development in assessment
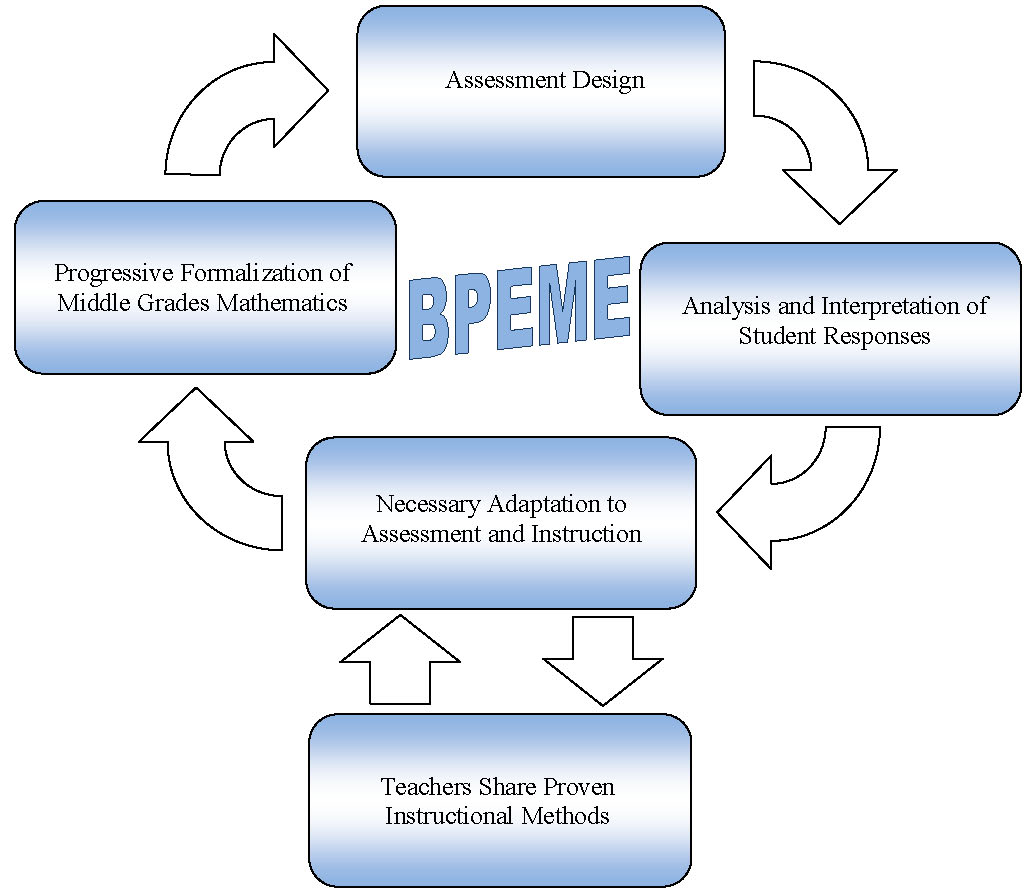
The professional development model for BPEME was based on a learning cycle that integrated teacher learning with assessment development in four inter-related phases (Figure 10). The first phase addressed essential concepts and skills in select areas of mathematics, elaborated using the principle of progressive formalization (described in more detail below). In the second phase, teachers selected, adapted and designed assessment tasks that could elicit a range of student strategies and representations within the domain of mathematics that teachers had previously explored and discussed in the previous phase. The third phase involved analysis and interpretation of the responses students made to the assessment tasks teachers designed for, and used with, them; additional attention was given to responses of students who were flagged by teachers as underperforming in their classrooms and on state assessments. The fourth phase involved teacher responses and adaptations to the assessment tasks and application of instructional strategies based on the interpretation of student responses. These adaptations focused on increasing access to mathematics for the students who had been identified by teachers in phase three. A spin-off phase resulted from these adaptations, during which teachers presented and discussed strategies they had found to be successful in supporting underperforming students.
This cycle was repeated several times in each of the mathematics domains over the course of the project. While each of these phases was theoretically distinct, they interacted with each other in practice through BPEME meetings and in the work of the teachers in their classrooms.
The BPEME model incorporated the professional development trajectory illustrated for CATCH. The Initiate and Investigate activities were included in the BPEME Assessment Design phase; the Interpret phase in CATCH was the Analysis and Interpretation phase in BPEME; and the Integrate activities from CATCH were addressed in the Adaptation phase in BPEME. The additional phases in BPEME were included to address the new program goals of enhancing teacher understanding of mathematics and closing the achievement gap. The cyclic approach allowed teachers to revisit assessment design principles for specific domains of mathematics.
Progressive formalization as a complementary design principle for assessment
The approach we used to explore the development of mathematics with teachers was based on Realistic Mathematics Education (e.g. Gravemeijer, 1994), particularly the principle of progressive formalization, a mathematical instantiation of constructivist learning theories (Bransford, Brown & Cocking, 2000). Progressive formalization suggests that learners should access mathematical concepts initially by relating their informal representations to more structured, pre-formal models, strategies and representations for solving problems (e.g. array models for multiplying fractions, ratio tables for proportions, percent bars for solving percent problems, combination charts for solving systems of equations, etc.). When appropriate, the teacher orients instruction to build upon students’ less formal representations. The teacher either draws upon strategies by other students in the classroom that are progressively more formal, or introduces the students to new pre-formal strategies and models. Because pre-formal models are usually more accessible to students who struggle with formal algorithms, they are encouraged to refer back to the less formal representations when needed to deepen their understanding of a procedure or concept. Pre-formal models also tend to involve a more visual representation of mathematical processes, which further facilitates student sense-making and understanding of related formal strategies. Through careful attention to students’ prior knowledge, expected informal strategies, and known pre-formal models, teachers can select and adapt formative assessment tasks that are more likely to elicit representations that are accessible to students.
Progressive formalization in an iceberg: Key professional development activities from BPEME
From our work in the CATCH project we recognized that limitations in a teacher’s understanding of mathematics content influenced his or her ability to select or design tasks that were accessible to various student strategies (e.g. connections). Even though the teachers in the project had strong knowledge of formal mathematics, and also saw value in the less formal strategies their students preferred, the teachers seemed to view the less formal strategies as a collection of convenient tools rather than as a significant part of the overall development of student understanding of mathematics.
Iceberg activity. To draw on the teachers’ collective understanding of the content domains of rational number, proportion and algebraic reasoning, we asked teachers to share and demonstrate their various strategies and representations for solving problems in these domains (each content domain was addressed in a separate cycle of BPEME activities). To deepen teachers’ understanding of mathematics, and to encourage their appreciation of pre-formal and informal models, we gave them challenging problems to solve, and allowed them to discover how they, like their students, were inclined to utilize less formal representations and strategies when faced with solving unfamiliar problems.
At various times throughout this activity, we would ask a teacher to share his or her strategy for solving the problem. The group then discussed the strategy and categorized it as informal, pre-formal or formal. In a number of cases, we found that teachers pre-formal strategies were sometimes more efficient and accessible to the group than the formal approaches.
As we focused on topics specific to middle grades mathematics, the teachers met with each other in smaller groups to discuss informal, contextual representations, and pre-formal strategies and models, that were related to a set of formal representations for a given topic (e.g. y = mx + b for Linear Functions). From these small groups, lists of representations were generated to share with the entire group. If one small group shared any strategies or representations that the rest of the group was not familiar with, a volunteer would present the new material to the large group (this happened more often than expected). Rich conversations occurred regarding the mathematics.
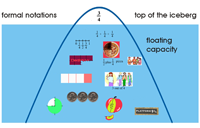
We then turned to a model that teachers could use to distinguish between informal, pre-formal and formal representations for different mathematical topics. We refer to this model as a “mathematical iceberg.” The “tip of the iceberg” represents formal mathematical goals. The pre-formal representations are at the “water line,” and informal representations are at the bottom (Webb, Boswinkel, & Dekker, 2008). The pre-formal and informal representations under the water line – the “floating capacity” – suggest that underneath the formal mathematics exists an important network of representations that can be used to increase student access to and support student understanding of mathematics (Figure 11). We gave the teachers the opportunity, in groups, to complete their own mathematical icebergs based on general subtopics in a given content area. Some groups took liberty with the metaphor and chose to use Colorado’s Rocky Mountains instead of icebergs (Figure 12), but, in either case informal representations were placed at the base, formal goals at the tip, and pre-formal models in between. Because of the need for each group to come to a consensus about the classification and placement of representations, the interaction within the groups was often lively and sustained for a significant period of time. Co-facilitators repeatedly remarked that teachers “were having great conversations about mathematics.”
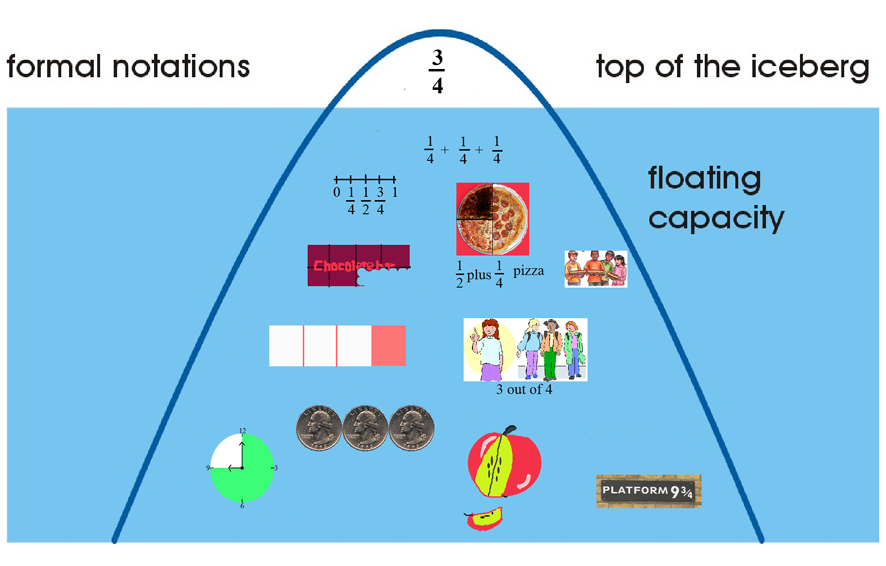

After initial drafts of the icebergs were constructed, each group had an opportunity to share, with the larger group, their iceberg and the mathematical representations they selected for each level. The teachers were given time to offer suggestions and feedback about the placement of models, representations, strategies and tools. As groups shared their icebergs, it also provided an opportunity for some teachers to teach their colleagues about less familiar strategies.
The BPEME professional development was the first time we used the “Build an Iceberg” activity with teachers. From the facilitators’ point of view, the icebergs offered a portrait of the teachers’ collective understanding for a particular content area, and helped us to flag aspects of mathematics that needed to be addressed in later sessions. As one might expect, the icebergs varied in quality and detail, but became a valuable tool for discussions about different content areas in middle grades mathematics that we would return to in successive BPEME cycles. The teacher-designed icebergs also became a reference that teachers used when suggesting different representations and strategies that should be taken into account when designing tasks to elicit a wider range of student responses.
Design and interpretation of mini-assessments. When we shifted our attention to assessment design, we used the same pyramid and trajectory of activities that we used with CATCH teachers, starting with the articulation of the levels of thinking in the pyramid and developing teachers’ interpretive skills regarding how tasks are designed to elicit types of student reasoning. With BPEME teachers, the prior content work with the Iceberg Model gave us all a common reference, allowing us to concentrate on assessment design within a particular domain of mathematics. This was a significant benefit, as we expected.
During the initial cycle, the iceberg activity followed the assessment pyramid leveling activity. Unexpectedly, a clash of two models occurred, creating confusion for some of the teachers since there was a subtle overlap between tasks found at the base of the pyramid (recall) and the representations found at the tip of the iceberg (formal). From this we realized that, during the initial cycle, it would be helpful to introduce the progressive formalization and assessment design in separate sessions, to allow time for reflection on the practical application of one model. In subsequent cycles, as distinctions are clarified through additional experience with task design and interpretation of student work, this separation of models is not needed.
The other challenge we encountered with assessment design was inadvertently trying to address too many topics in the same assessment. Our first attempt at collaborative assessment design in BPEME was a set of grade-level diagnostic assessments that could be used as pre-assessments at the beginning of the school year. We found out, however, that the parameters for a diagnostic assessment were too ambitious, resulting in the production of lengthy assessments that left little time for teachers to select or develop Level II and III questions.
In an attempt to keep the process focused and productive, we decided, in later iterations of assessment design, to restrict the design goal to mini-assessments, containing only 3 to 6 tasks addressing one topic within a content domain. Each mini-assessment needed at least one Level II or III task and had to use at least one relevant problem context. Since, over the course of the project, many teachers described that their increased use of pre-formal models in the classroom allowed students who consistently struggled with proportional reasoning to engage in solving more context-based problems, we also asked teachers to include some tasks that were accessible to pre-formal solution strategies. Given the opportunity to focus on one topic for a limited set of tasks, the design groups were much more successful in creating assessments that applied the design principles of progressive formalization and assessing student understanding.
These teacher-designed mini-assessments became a source of in-class experimentation (similar to the CATCH project) and were a catalyst for school-based collaboration around assessment design, student responses, and proposed instructional responses. BPEME facilitators sat in on many of these school-based sessions and encouraged teachers to share their findings with the larger group at the district wide meetings. In the final year of BPEME these showcase sessions emerged as one of the most popular sessions as indicated on teacher surveys and signaled a shift in the project toward a more distributed leadership model as we approached the final summer session.
Using icebergs to build long learning lines for formative assessment
Ideally, to leverage the relationship between mathematics content, formative assessment, and instructional decisions, professional development activities should promote teacher awareness of how instructional activities can be organized according to long learning lines within a content domain (van den Heuvel-Panhuizen, 2001). If one assumes that a characteristic of effective formative assessment is the ability to relate students’ responses to instructional goals, and knowing the instructional responses that promote student progress towards those goals, then conceptual mapping of the mathematical terrain should support how teachers interpret student responses and adapt instruction accordingly. As argued by Shepard (2002), when teachers develop an understanding of the progression of content in a particular subject area, they use these learning progressions to move backward and forward in framing instruction for individual students (p. 27).
Learning line activity. Through the sustained study of progressive formalization across the BPEME cycles, we found that teachers were able to recognize informal, pre-formal and formal representations in their instructional materials (fortunately, some teachers used materials that made use of these less formal representations). Teachers also explained that they perceived gaps in their instructional materials, sections that they felt needed additional representations of one type or another to bridge these gaps. Therefore, as a unique and somewhat ambitious attempt to synthesize what the teachers had learned, we decided to design a Learning Line activity as a culminating event for the project during the final BPEME summer workshop. The outcome of this activity would be Internet-ready icebergs that would illustrate potential instructional sequences for 10 different topics. Each of these icebergs were to include: detailed descriptions and/or visuals of the key representations, identification of crucial learning moments (marked in red border), instructional activities to address one or more perceived gaps, and several mini-assessments that could be used to document student progress. Links could also be provided to relevant applets that could be used to enhance student learning.
There were several major design obstacles that had to be addressed to ensure the success of this activity: 1) To produce a technology-based resource, we needed access to Internet-ready computers, printers, and scanners; 2) We needed web-page development software that teachers could quickly learn and use to produce their materials and; 3) We required sufficient design and production time so that the teachers would be satisfied with the final product.
The first challenge was a resource issue that we were able to address by finding an adequate professional development site. The third challenge required additional planning to evaluate the feasibility of this activity. Two of the district instructional coaches who were part of the BPEME leadership team, Michael Matassa and Paige Larson, agreed to develop a prototype of the final product using the web-authoring features of Inspiration®, a concept-mapping software tool. As they developed the prototype they kept track of the time demands for the overall product and the list of proposed resources. The topic they selected for the prototype was Patterns and Generalization[2]. At various stages of developing the prototype it became clear that the software tool was somewhat user-friendly and intuitive (this addressed challenge 2), and that the final product would be a resource that offered much greater potential for cross-district communication and ongoing usability than collecting hard copies of summer institute resources.
The introduction of the Learning Line activity was phased in over the summer institute, with the last three days devoted entirely to the planning, design, production, and presentation of the learning line. Knowing in advance the characteristics of the culminating product and the requisite intellectual demands that would be placed on teachers influenced the overall structure of the summer session, the sequence of activities, and the design of specific sessions on learning lines and their role in supporting formative assessment. The activity was first introduced with an overview of the goals of the activity, expected products, and an overview of main features of the prototype learning line. A brief session on the essentials of the web-design software was also included. The teachers identified rational number, algebra, operations with integers, and the Pythagorean Theorem as topics of interest (the latter two were not topics we had explored in the design cycle) and then set out to complete their learning lines.
What participants seemed to appreciate most about the activity was that it was an opportunity to use the design principles and decision processes that had been learned over the course of BPEME to create something that seemed practical and readily available to colleagues. As new insights about assessment and mathematics were elicited in BPEME, teachers wanted more time for collaborative planning so these ideas could be incorporated into future lessons. Essentially, the learning line activity was an opportunity for collaborative planning with an underlying set of design principles and desired outcomes.
During the development of the prototype we realized that the design groups would be in a better position to make sense of what they had created. There was no guarantee that the ideas expressed in each iceberg could be communicated to groups that did not contribute to its development. To help facilitate improvements in communication and design, we organized showcase sessions so that other groups could ask questions of clarification, suggest corrections, or flag aspects of the learning line that did not make sense. The leadership team also circulated among the groups to offer ongoing feedback and suggestions throughout the process. Some design teams had the opportunity to revise and improve their learning lines, and other groups needed the entire time to develop the first version of their learning line[3].
For the participating teachers, the learning line activity was an open-ended Level III problem that required substantive discussions and justification of decisions about mathematics curriculum, instruction, and assessment. In a manner similar to when teachers assign projects to their students, we outlined expectations for the learning line activity, offered an exemplar, and created instructional space to offer ongoing support and feedback as groups deliberated different options for curriculum plans, assessment questions, and progressive formalization for a particular content area. Likewise, these products are also representative assessments of the mathematics the teachers learned throughout BPEME, their understanding of design principles for assessment, and how they intend to use these ideas in their classrooms.
Reflections on the BPEME model for professional development
5Often with professional development the products that teachers collect end up in a 3-ring binder to find a place on a resource shelf. These resources seldom find their way into teachers’ classrooms. Quite unexpectedly, because of the dual work with content and assessment, teachers were given an opportunity in BPEME to develop an instructional resource that could be shared beyond their school and district boundaries. These products serve multiple purposes. First, they serve as a model for a resource developed by teachers that can be used to support other teachers’ formative assessment practices. Second, they are adaptable resources that can be edited, improved and appended as time permits. Teachers can add additional assessments as they are developed and strengthen learning lines that are needed. Third, they represent an application, by teachers in the United States, of design principles for assessment and instruction that were originally developed by research faculty from the Freudenthal Institute. That is, these design principles are accessible to novice and experienced teachers. Teachers use these principles to interpret instructional materials, assessment tasks, and classroom practice. Lastly, these resources serve as an authentic assessment that represents teachers’ understanding of assessment, mathematics, and instructional approaches that support student understanding of mathematics.
The impact of BPEME professional development on teachers’ assessment practice and student achievement has been reported elsewhere (Webb, 2008) and additional results are forthcoming, yet these teacher artifacts are compelling portraits of the impact of BPEME on participating teachers’ conceptions of how students learn mathematics and the role of formative assessment. They further demonstrate that teachers are interested in and, with the proper resources, can engage in, the design of assessment and instruction that supports student understanding of mathematics.
Concluding Remarks
6The design process for professional development is quite different from the design process for, say, assessment design. Professional development programs rarely have a sustained audience that allows a design team to test the relative merit of activities to meet the learning objectives established for teachers. Furthermore, during challenging economic times, school districts and funding agencies are less inclined to fund professional development and often reallocate funds to higher priorities such as maintaining teacher positions and classroom facilities. Professional development, unfortunately, is often seen as a luxury rather than a necessity for teacher growth. With this in mind, I have been quite fortunate to have several opportunities to revisit and re-evaluate assumptions about the types of professional development experiences teachers need to improving their classroom assessment practices.
It is quite likely that the professional development model for BPEME could be used with other disciplines (cf. Hodgen & Marshall, 2005), as there are close associations between the levels of mathematical reasoning articulated in the assessment pyramid and expectations for student literacy in science, language arts, and other domains. Overarching goals of the discipline (e.g. scientific inquiry) would be exemplified through tasks located in the higher levels of the assessment pyramid. Even though progressive formalization might not be the best way to characterize student learning in science and other disciplines, similar types of long learning lines could be constructed based on how students come to understand core ideas of the discipline.
Acknowledgements
7This article has benefitted greatly from encouragement and feedback offered by Hugh Burkhardt, Paul Black, Truus Dekker, Beth Webb, and anonymous reviewers for Educational Designer.
The work described in this article was the result of ongoing collaboration with colleagues and friends from the University of Wisconsin and the Freudenthal Institute for Science and Mathematics Education. Thomas A. Romberg and Jan de Lange were co-directors of the CATCH project. I am grateful for their early encouragement and support in the study of classroom assessment. The CATCH and BPEME projects also benefitted from ongoing collaboration with research faculty from the Freudenthal Institute, some of the finest designers in mathematics assessment and curriculum that I have had the privilege of working with. Contributing research faculty from the FiSME included Mieke Abels, Peter Boon, Nina Boswinkel, Truus Dekker, Els Feijs, Henk van der Kooij, Nanda Querelle, and Martin van Reeuwijk. Likewise, the work of the BPEME project would not have been possible without the contributions of Anne Dougherty, Paige Larson, Michael Matassa, Mary Nelson, Mary Pittman, Tim Stoelinga, and the many inspiring mathematics teachers from the Boulder Valley School District who trusted the design team and challenged us to rethink our conceptions of what professional development should be.
References
8Annenburg Media (2009). http://www.learner.org/ [retrieved on February 9, 2009].
Black, P., & Wiliam, D. (1998). Assessment and classroom learning. Assessment in Education, 5(1), 7-74.
Black, P., Harrison, C., Lee, C., Marshall, B., Wiliam, D. (2003). Assessment for Learning: Putting it into Practice. New York: Open University Press.
Dekker, T. (2007). A model for constructing higher level assessments. Mathematics Teacher, 101(1), 56 – 61.
Dekker, T., & Feijs, E. (2006). Scaling up strategies for change: change in formative assessment practices. Assessment in Education, 17(3), 237-254.
Gravemeijer, K.P.E. (1994). Developing Realistic Mathematics Education. Utrecht: CD-β Press/Freudenthal Institute.
Her, T., & Webb, D. C. (2004). Retracing a Path to Assessing for Understanding. In T. A. Romberg (Ed.), Standards-Based Mathematics Assessment in Middle School: Rethinking Classroom Practice (pp. 200-220). New York: Teachers College Press.
Hodgen, J., & Marshall, B. (2005). Assessment for Learning in Mathematics and English: contrasts and resemblances. The Curriculum Journal, 16(2), 153-176.
Lesh, R., & Lamon, S. J. (Eds.) (1993). Assessment of authentic performance in school mathematics. Washington, DC: AAAS.
Otero, V. (2006). Moving beyond the “get it or don’t” conception of formative assessment. Journal of Teacher Education, 57, 247-255.
Romberg, T. A. (Ed.) (1995). Reform in school mathematics and authentic assessment. Albany, NY: SUNY Press.
Romberg, T. A. (Ed.) (2004). Standards-Based Mathematics Assessment in Middle School: Rethinking Classroom Practice. New York: Teachers College Press.
Shafer, M. C., & Foster, S. (1997, Fall). The changing face of assessment. Principled Practice in Mathematics and Science Education, 1(2), 1 – 8.
Retrieved on April 23, 2009 from http://ncisla.wceruw.org/publications/newsletters/fall97.pdf.
Shepard, L. A. (2002, January). The contest between large-scale accountability testing and assessment in the service of learning: 1970–2001. Paper presented at the 30th anniversary conference of the Spencer Foundation, Chicago.
van den Heuvel-Panhuizen, M. (2001). Learning-teaching trajectories with intermediate attainment targets. In M. van den Heuvel-Panhuizen (Ed.), Children learn mathematics (pp. 13–22). Utrecht, The Netherlands: Freudenthal Institute/SLO.
Webb, D. C. (2008, August). Progressive Formalization as an Interpretive Lens for Increasing the Learning Potentials of Classroom Assessment. Poster presented at the Biennial Joint European Association for Research in Learning and Instruction/Northumbria SIG Assessment Conference, Potsdam, Germany.
Webb, D. C., Boswinkel, N., & Dekker, T. (2008). Beneath the Tip of the Iceberg: Using Representations to Support Student Understanding. Mathematics Teaching in the Middle School, 14(2), 110-113.
Webb, D. C., Romberg, T. A., Burrill, J., & Ford, M. J. (2005). Teacher Collaboration: Focusing on Problems of Practice. In T. A. Romberg & T. P. Carpenter (Eds.), Understanding Math and Science Matters (pp. 231-251). Mahwah. NJ: Lawrence Erlbaum Associates.
Webb, D. C., Romberg, T. A., Dekker, T., de Lange, J., & Abels, M. (2004). Classroom Assessment as a Basis for Teacher Change. In T. A. Romberg (Ed.), Standards-Based Mathematics Assessment in Middle School: Rethinking Classroom Practice (pp. 223-235). New York: Teachers College Press.
Wiliam, D. (2007). Keeping learning on track: classroom assessment and the regulation of learning. In F. K. Lester Jr (Ed.), Second handbook of mathematics teaching and learning (pp. 1053-1098). Greenwich, CT: Information Age Publishing.
Footnotes
[1] For more details about the CATCH project, and related resources and results, see Webb, Romberg, Dekker, de Lange & Abels (2004), Dekker & Feijs (2005), and http://www.fi.uu.nl/catch/
[2] The final prototype can be found at: http://schools.bvsd.org/manhattan/BPEME/learning%20trajectories/patternsgeneralizationPM/pattgenMP.htm
[3] Other examples of teacher-designed learning lines can be found at the BPEME website: http://schools.bvsd.org/manhattan/BPEME/INDEX.HTM
About the Author
9David C. Webb is an Assistant Professor of Mathematics Education at the University of Colorado at Boulder and is also the Executive Director of Freudenthal Institute USA. His research focuses on teachers’ classroom assessment practices, curricula that support formative assessment, and the design of professional development activities. Recent research projects have also included the design and use of tasks to assess student understanding in the contexts of game design, computer programming, and interactive science simulations.
He taught mathematics and computer applications courses in middle and high school in Southern California. He currently teaches methods courses for prospective secondary mathematics teachers, and graduate level seminars that focus on research and design in assessment and the nature of mathematics and mathematics education.