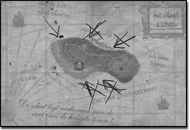
The research we report on here started as a study to improve a computer game called Treasure Island[1] (see Figure 1). In this game, captain Kwark sails around the island of Lund, which has three towers: the lighthouse, the tower of Zilt (a pirate), and the church tower. A little circle on the map shows where the captain's boat is. By moving the little circle, one changes the place of the boat. When the player clicks on a pair of binoculars, the towers are shown from Kwark's point of view. In order to stimulate thinking, this image disappears when the boat is moved and only comes back when the binoculars are clicked again.



The actor's and observer's point of view
A geometry applet as an example
Nisa Figueiredo and Frans van Galen
Freudenthal Institute (FIsme), Utrecht, Netherlands
Koeno Gravemeijer
Eindhoven School of Education, Netherlands
Abstract
1When designing mathematical educational tasks, a designer tries to anticipate how students will react. Students, however, may look at a task in a way that differs much from how teachers or instructional designers look at it. In relation to this, one speaks of the difference between the actor's and the observer's point of view. In this article, we elaborate on this distinction, outlining a theoretical and empirical perspective on the differences between these two points of view. To do so, we use the data from a small scale teaching experiment with a geometry applet that we had designed.
Introduction
2According to socio-constructivism, students construct their own mathematical knowledge. This is also the basic idea of Realistic Mathematics Education (RME), the domain-specific instruction-theory that has been developed in the Netherlands over the past 40 years. According to this theory, students should be given the opportunity to reinvent mathematics. Designers of educational tasks adhere to the principle of guided reinvention (Freudenthal, 1973). They try to help students to construct new and important mathematical ideas by providing them with suitable tasks.
The problem with designing for mathematics education is that the designer already knows the mathematical concepts, which are the goals of the tasks. Designers have to forget this, in a sense, and put themselves in the shoes of the learner. This asks for a shift in perspective, which is called a shift from an observer's point of view to an actor's point of view (Gravemeijer, 2004; Cobb & Bowers, 1999; Cobb, 1987). When designing computer tasks, where students work largely on their own, taking into account the actor's perspective is even more important. In more traditional educational tasks, the teacher is present and can guide the learning process.
In this article, we try to substantiate the differences between an actor's and an observer's point of view by analysing a teaching experiment with a geometry applet.
It is worthwhile to analyse the differences between these two perspectives for two reasons. First, it may yield valuable information for educational designers. They should be aware of the fact that students may interpret a task in a way that differs from how it was intended. Secondly, it may yield valuable information to teachers. By definition they have much more knowledge about mathematics than the students, and their task is to change the way students look at things mathematically. If a teacher is not aware of how his own perception of the world may be different from the students' perception, this may lead to misunderstandings, where students give solutions that are plausible from their perspective, but are considered by the teacher to be incorrect.
Research context
3An important aspect of geometry has to do with understanding and describing the relative position of objects in space, and the position of an observer in relation to those objects. This leads to activities where students take different positions in space, and observe and describe how they see objects from those positions (Hershkowitz, Paszysz & Dormolen, 1996; Heuvel-Panhuizen & Buys, 2005). The real world is the best setting for such activities, but meaningful activities are also possible in a computer learning environment. Computer programs, or applets, give students the possibility to analyse how they see things in ways which are not always possible in the real world.
 Click to run the Applet
The live applet can be run from the online version
Click to run the Applet
The live applet can be run from the online versionIn an earlier study (Van Galen, 2000), it was found that students did not show much reflection when they played the game. It was decided to develop a new set of questions and investigate the possibilities of the applet to foster reasoning with “vision lines'. In the design process, we analyzed the context and wording of the tasks carefully in order to make sure they would fit what students knew and were capable of, stimulating them to use their informal knowledge. In doing so, we developed a hypothetical learning trajectory (cf. Simon, 1995). When we tested our new tasks, however, the students appeared to come up with solutions and ways of reasoning we had not expected, and some of which we couldn't even explain at that moment.
When we studied the reactions of the students, it became clear that several of them illustrated how we, as designers, had looked at the tasks from a mathematically more sophisticated point of view, whereas the students interpreted the situation in very concrete terms. So there was a difference between our perspective as observers, watching the students solving the problems, and the perspective of the students as actors. The focus of our study then changed towards trying to explain this difference.
Theoretical framework
4Present-day teaching and learning theories are dominated by the idea that students construct their own knowledge. According to socio-constructivism, these constructions are influenced by the students' interaction with the learning environment. Learning mathematics is understood as a process where students, as a group and together with the teacher, develop mathematical knowledge. Cobb, Yackel, and Wood (1992) call this knowledge taken-as-shared because it is not possible to know if this knowledge is in fact shared. Teacher and students construct knowledge together, in a process that is influenced by the socio-norms and socio-mathematical norms of the class. These norms refer to the expectations that teachers and students have of each others role, they refer to what are acceptable explanations and justifications, and they refer to what mathematics is and how it should be learned.
The idea that students construct their own knowledge is in agreement with Freudenthals' idea of mathematics as a ‘human activity’ (Freudenthal, 1973), which constitutes the basis of RME. According to this idea, students should be given the opportunity to learn mathematics by mathematizing, which includes mathematizing everyday life subject matter as well as mathematizing their own mathematical activity. It is important that students perceive the starting point for this activity as experientially real.
What is real for a particular student, however, does not have to be real for another student or for the teacher. In relation to this, Van Hiele (1973) has pointed out that students and teachers have different frames of reference, caused by a difference in their level of thinking. Van Hiele analyzed the communication processes between teacher and students and found that the words they use may have different meanings (Gravemeijer, 1994). The mathematical knowledge which teachers have, and students do not have, provides them with different frames of reference from which concepts derive their meanings.
This difference in frames of reference is also the problem pointed out by Cobb, Yackel and Wood (1992) who take the use of concrete materials such as the Dienes blocks as an example. They argue that students do not know yet the decimal system, which they ought to see in the materials. Bereiter (1985) called this the learning paradox, which is explained by Cobb et al. (1992, p. 5) as follows:
The assumption that students will inevitably construct the correct internal representation from the materials presented implies that their learning is triggered by the mathematical relationships they are to construct before they have constructed them. (…) How then, if students can only make sense of their worlds in terms of their internal representations, is it possible for them to recognize mathematical relationships that are developmentally more advanced than their internal representations?
As an alternative we may try to foster a situation in which students construct more sophisticated mathematics by themselves. In order to do so, teachers and designers have to anticipate what students might do and what they might think when they participate in the instructional activities we have in mind for them. This boils down to what Simon (1995) calls hypothetical learning trajectories. To develop these, the designer should try to take the student's point of view – the actor's point of view (Gravemeijer, 2004; Cobb & Bowers, 1999) - and try to envision which knowledge and insights students will bring to the tasks, which meanings they will give to contexts, etc. In this process, the instructional designer tries to ‘see’ how the student sees the mathematics from his/her perspective and at the same time see ‘our’ mathematics in the work of the students. This is what Ball (1993. p. 159) calls a bifocal perspective:
Perceiving mathematics through the mind of the learner while perceiving the mind of the learner through the mathematics.
This, however, is not easy, as the instructional designer and the teacher will have to stand in the shoes of someone with less knowledge. They know the mathematics and, therefore, ‘see’ the mathematics in the tasks, which is not the case for the students.
Besides these differences in mathematical knowledge, there are also differences in expectations. The teacher or instructional designer has certain expectations about, for instance, how far the context should be taken into account when solving a mathematical problem, and these expectations may differ from those of the students. In relation to this, Cobb and Yackel (1996) speak of socio-mathematical norms. Gravemeijer (2004, p. 6) uses the following word problems from the research of Verschaffel, Greer and De Corte (2000) to illustrate this:
Jim has 5 planks of 2 metres. How many planks of 1 metre can he make?
John has 4 planks of 2 1/2 metres. How many planks of 1 metre can he make?
Verschaffel et al. (2000) point out that students usually give ten as the solution for both problems, while this is not a realistic answer for the second problem. The correct solution is eight since one has to get whole planks, and, therefore, students should take the context into account. In the first problem, however, even though everybody is convinced the solution should be ten, the context is also ignored up to a certain point. For this answer does not take into account the width of the cut. So it seems, there is an implicit understanding, that this fact should not be taken into account.
In this section we have outlined two aspects in which the actor's point of view and the observer's point of view may differ. These concern differences in frames of reference due to differences in mathematical knowledge and differences in socio-mathematical norms. We shall now turn to the teaching experiment with the geometry applet to bring the two things together in the discussion section.
The tasks: point, line, region
5The new series of tasks[2] we designed starts with a story about captain Kwark who sails around an island that has three towers: a lighthouse, a church tower and the tower of Zilt, the pirate.
The first task is similar to the one of Figure 1. The computer screen shows a picture of the island with the three towers and the question is: “From which place in sea can this picture have been taken?” The second task shows a picture of the three towers and a map of the island, with a point highlighted from where Kwark is said to have taken the picture. The question is whether the picture could have been taken from that point. In this task, the binoculars are not available anymore, so it is not possible to check the situation with the binoculars.
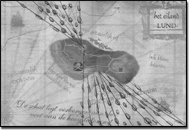
In the following tasks, no picture is given. Task 3 (Figure 2) shows the map and the binoculars. The question is: “Look for a place where you can only see two towers through the binoculars.” The designers had in mind those places where one of the towers is hidden behind another one. A little circle on the map tells where the boat is and by clicking on the binoculars the student gets an image of the towers from that point of view. In Task 4, the students no longer have the binoculars tool available. On their worksheets, they have a map of the island and they are asked to mark all possible spots from which Kwark cannot see the church tower. This task asks for a generalization of the answer to Task 3.
In Task 5, students can use the binoculars again. The question is: “Look for a place where you can take a picture with the lighthouse somewhere between the other two towers.” Task 6 asks again for a generalisation. The students are asked to mark on their worksheet all possible places from which the captain would see the lighthouse between the other two towers.
Finally, Task 7 turns the situation around. Now the question is not about a picture taken from the boat, but about what Zilt can see from his tower. The text says that Zilt sees a big ship between the lighthouse and the church tower. Students are asked to mark all possible places where this ship can be on their worksheet map.
The tasks are designed in such a way that Tasks 2, 4 and 6 ask for a generalisation of the answer to the task that precedes it. Tasks 1 and 2 are about looking from a given point; Tasks 3 and 4 are about lines; and Tasks 5, 6 and 7 are about regions. There were 10 tasks in total, but we will leave the last three tasks out of our discussions.
In the tasks, a line is seen from the designers - mathematical - perspective as (1) a ‘vision line’ or line of sight, but (2) also as a set of points from where one can see something in a certain way. A region is a set of points for which a certain rule applies, such as that from each point one sees something in a certain way. A region is bordered by lines with specific properties.
Research method
6The research we report here can be characterized as an explorative qualitative research with a participant observer, and is very similar to what Steffe (1983) calls a ‘teaching experiment’. In such a teaching experiment, the researcher interacts with one or two students in order to explore their reasoning, audio- or video-taping the activity for a retrospective analysis (Steffe, 1983; Steffe & Thompson, 2000). The goal of the analysis is to understand what students did and why, trying to understand the mathematical reality of the students.
The tasks that were developed around the island applet were presented in two sessions to grade 5 students from a primary school. Ten students participated, six boys and four girls, working in pairs. The students worked approximately half an hour in each session, with an interval of one week between the sessions. All group work was video-taped. The students were asked to work together on the tasks, even though they both had their own worksheets, with spaces for draft sketches and final answers. By giving each student a worksheet we hoped to stimulate each one to work on the tasks and not only the one with the worksheet.
The researcher was sitting next to the students and tried to interfere as little as possible. As the original goal of the study was to improve the computer tasks, students were expected to work autonomously. The researcher only asked questions when students had a solution (right, wrong or incomplete) or when they did not know how to continue. The goal was, on the one hand, to understand the students' thinking, and, on the other hand, to stimulate reflection and to foster higher-level thinking.
The researcher asked the following types of questions:
- Requests for explanation, like: “How did you come to that solution?”
- Questions about the completeness of answers, like: “Are those all the possible places?” Or: “What about this place here?”
- Questions about evidence, like: “Can you show me why this is correct?”
- Questions stimulating cooperative work, like: “I see differences between your solutions, so have a look at it together”. Or: “I heard him saying that…, what does he mean? See if you both agree on that”.
The data consisted of video-tapes of the groups' work, the students' worksheets and the notes of the researcher.
The method for data analysis was based on the method of Cobb & Whitenack (1996), which in turn is based on the constant comparative method of Glaser and Strauss (1967). First, we made small reports on the work of the children, based on the field notes, global analyses of the video-tapes and the worksheets of the students. Using these reports, we found certain aspects which showed up repeatedly in different groups and tasks and which ought to be analyzed more carefully. This gave us a first frame to analyse the worksheets and video-tapes once again.
In this first phase of the analysis, we made a detailed description of the students' work for each task, complemented with pieces of a transcript and a reconstruction of the symbolizing activity of each student. In this manner, we were able to identify within each aspect certain patterns which were formulated in terms of conjectures, about what actually happened.
In the second phase, we went back to the data to test the conjectures. We asked ourselves: “Does this indeed happen repeatedly? And where it does not happen, is that contradicting our conjecture?” While testing the conjectures we noticed new things and formulated new conjectures to be tested in the other tasks. Working this way, we came to a preliminary list of what we called explanatory observations.
Finally, these explanatory observations became data and were analyzed at a more meta-level: “How do the findings relate to each other, and how are they all related to the theoretical framework?”
Students at work – the findings
7In this section we analyse the students’ answers to Tasks 3 up to 7, with an emphasis on the problems that ask for a generalization (Tasks 4, 6 and 7). We discuss how the responses of the students differed from what the instructional designers had anticipated, and how these differences can be explained by making a distinction between an actor’s and an observer’s point of view.
A different interpretation of ‘seeing’
We find a first case in the different way that students and designers interpreted the word ‘seeing’ in the problems. With ‘seeing’ - for example in: “On that spot the captain does not see the church tower (but he sees the other towers)” - the designers meant looking-around-and-seeing, while for students it meant keeping your head still. This looks like a simple misunderstanding but it is more than that. Our explanation is that the designers used a mathematical interpretation of the context, while the students interpreted the context in more concrete terms.
A first example can be found in Task 4, where students have to show on the map of their worksheet where the captain can be such that he cannot see the church tower. Silvana comes up with two possibilities: “there is a tower in front, or the vision field is too small”. Her first answer is what the designers had in mind but with her second answer she is saying that the church tower falls outside the captain’s field of vision while he is keeping his head still.
This interpretation of ‘seeing’ also explains what Annika does in this same task. She draws five arrows that show the direction in which the captain may be looking (see Figure 3). Two of those arrows are next to the church tower but according to Annika the captain can not see the tower from that place. She explains how the field of vision plays a role:
Annika: “Because, if you look from here, make a photograph, you can't see that (the church tower). (…) if I make a picture there (she makes a frame with her hands looking through it with one eye as if she is taking a picture), then I see those two, but not that one.”
The solutions the designers had in mind here were the line segment through the church tower and the tower of Zilt and the line segment through the church tower and the lighthouse. The students, however, came up with solutions that originated from a more literal interpretation of ‘seeing’: there are always things you cannot see because they are to the left, to the right or behind you.
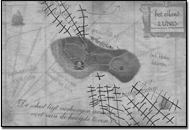
Another example can be found in Task 7. The text says that Zilt sees a big ship somewhere between the church tower and the lighthouse. Students interpret this as if Zilt can see the two towers and the ship at the same time, without moving his head. For this reason, three of the five pairs of students do not draw the lines as far as the church tower. Figure 4 shows the work of Han who is very explicit about Zilt’s field of vision.
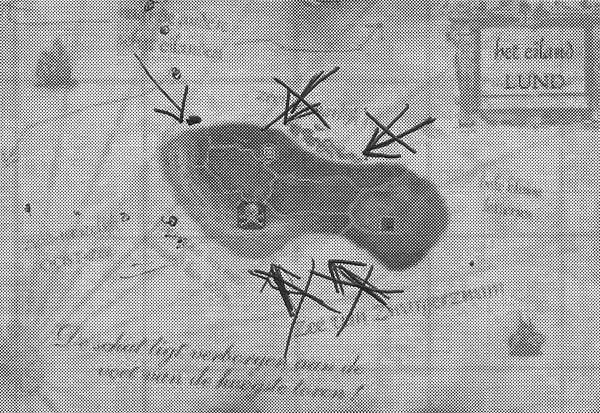 Figure 3. Task 4: Captain Kwark sees two towers, but he does not see the church tower. Where can he be? Annika’s solution
Figure 3. Task 4: Captain Kwark sees two towers, but he does not see the church tower. Where can he be? Annika’s solution  Figure 4. Task 7: Pirate Zilt sees a big ship between lighthouse and church tower. Where can it be, this ship? Han’s solution.
Figure 4. Task 7: Pirate Zilt sees a big ship between lighthouse and church tower. Where can it be, this ship? Han’s solution. Han: (pointing at the church tower and the lighthouse)
“He looks from his tower and he sees these two.”
Leo: “Yes, he can decide for himself to which tower he looks.”
Han: “No, look, (he reads) he sees a big ship between the lighthouse and the
church tower. If he looks at this, he might also see that as well, I think, and
that, and there in between there's where the ship should be.”
Leo: “Or he has a curved look”.
Han: (laughs) “Very curved…(pointing to the church tower)
There you have the mirror! (laughs).”
Also in this task, students interpret ‘looking’ and ‘seeing’ differently than the designers expected. The latter thought of the region limited by the lines one can draw between the Zilt tower and each of the other two towers. Whether Zilt could see the lighthouse and the church tower without moving his head did not matter in their interpretation of ‘seeing’. The students, however, interpreted this idea in a static way: it is about what can be seen within the vision field of someone who keeps his head still.
We can understand this difference in interpretation when we take into account the difference in levels of mathematical thinking of students and designers. The designers had interpreted the situation in mathematical terms - lines, angles and regions - which brought them to a dynamic interpretation of ‘seeing’. For the students, who did not have this mathematical knowledge, such an interpretation was not obvious. Their interpretation was based on the context and the computer program and on their knowledge of ‘seeing’ in the real world. It is highly probable that this interpretation of students was partly influenced by the computer program itself, as the binoculars give a static picture of the towers. The students often call it, ‘a photo’. Their static interpretation of ‘seeing’ is, therefore, not so strange. A way to avoid this misunderstanding between designers and students could be to make it possible to change the direction of the binoculars in the computer program. That would make it clearer that ‘seeing’ here also means ‘looking around’.
It should be noted, incidentally, that the angle of view provided by the computer binoculars is in fact too wide for real binoculars. If we compare it to camera lenses, the binoculars resemble a wide angle lens more than a telephoto lens. The choice to use binoculars instead of a camera in the computer program had to do with the context, as binoculars fit better the context of a captain sailing around an island .
We are aware that this misunderstanding between designer and student could probably be avoided partly by being more explicit in the text about the meaning of the word ‘seeing’, or maybe by using a very different word for it. This, however, only stresses the point we want to make: the designer (observer) had a different interpretation of the tasks’ questions than the students (actors) and that is due to the fact that the designers can ‘see’ the mathematics in the problems and therefore think of the problems’ situation in a more mathematical manner.
A different concept of ‘line’ and ‘region’
8The way students represented their solutions on the worksheets was also different than what the designers had expected. The students use representations that at first sight look strange and cumbersome, but that make sense when one considers that the students use a different concept of ‘line’ and ‘region’ than the designers.
An example can be seen in the work of Maura (Figure 5). She does not simply colour the regions, but she draws a lot of lines with dots on it. Maura was not an exception, as half of the students did this in at least one of the three generalisation tasks (Tasks 4,6 and 7). There is a student that even does so in all three tasks and also a pair of students that draw these points as boats. Lukas' solution for task 6 (Figure 6) is another example.
A first question that arises is why she and other students felt the need to draw dots or marks on the lines. Our interpretation is that lines for the students are first of all lines of sight: they denote looking directions. The place from where someone is looking has still to be indicated separately. With their dots and marks students, however, do not only mean those particular places. It is their way to show that there are a lot of places. As they do not yet see a line as an infinite set of points, they come up with their own representations.
 Figure 5. Task 6: Captain Kwark sees the lighthouse between the other two towers. Where can he be? Maura’s solution.
Figure 5. Task 6: Captain Kwark sees the lighthouse between the other two towers. Where can he be? Maura’s solution. Figure 6. Task 6: Captain Kwark sees the lighthouse between the other two towers.
Where can he be? Lukas' solution.
Figure 6. Task 6: Captain Kwark sees the lighthouse between the other two towers.
Where can he be? Lukas' solution.The fact that in Task 4 students easily change their solution from one spot to a set of spots when questioned by the researcher, also supports this interpretation. The task was to point out the places from where the captain could not see the church tower. At first, all students only pointed out single points; only one student came up with a line as solution. The other students indicated a single point behind each of the other two towers. The researcher responded to this by asking about another place just behind these points. Most of the students reacted to this in a similar way as Ricky:
“Oh, that doesn't really matter. Just on this line then”.
Only Silvana reacted with surprise.
Silvana: “He can not be here too (further back on that line), because
he would look in the same line, and then you can better do like, here a
dot, there a dot, there a dot” (she draws dots behind each other in a line
– see figure 7).
Observer: “But aren’t those different places?”
Silvana: “Yes, off course, but that’s a bit unfair, actually.”
Observer: “But these
are different places.”
Silvana: “Yes, but I don’t think that’s the purpose
of it.”
Observer: “Why not?”
Silvana: “Well, then you can just… like
this, very small dots, and than you can do a thousand of those.”
Silvana thinks that all those spots behind each other belong to the same solution and therefore she finds it “a bit unfair” to draw more spots in the same direction. So Silvana is aware that there are many spots where the captain can be - there are “a thousand of those” - but she marks only one spot because it is impossible to mark them all. The other students do not find this a problem as they give a different meaning to those dots and marks. They are not seen as ‘the solutions’ but they are given as examples, showing that there are many spots.
 Figure 7. Task 4: Captain Kwark sees two towers, but he does not see the church tower. Where can he be? Silvana’s solution.
Figure 7. Task 4: Captain Kwark sees two towers, but he does not see the church tower. Where can he be? Silvana’s solution.We suggest a similar interpretation for the fact that students do not just colour a region but instead draw a lot of different lines. Examples can be seen in Figure 5 and Figure 6, from Maura and Lukas, who worked separately. In Task 6, the question is where the captain can be such that he can see the lighthouse somewhere between the other two towers. From the perspective of the designers, the correct answer is to draw two regions, one above and one under the island, limited by the lines that go through the towers. From their perspective it is enough to draw these lines and colour the region in between. There was only one student who directly gave a region as solution to the problem.
Most students started to point out single spots, only to draw lines through these points afterwards. To indicate that there are many places from where the captain can see the lighthouse in between the other two towers, they drew a series of lines. Our interpretation is that students used these lines to indicate the direction in which the captain is looking. Maura draws her lines with a ruler and let them pass through the lighthouse. Lukas draws some parallel lines but his reasoning was probably not very different from that of Maura. In Task 7, Han is also very explicit about the fact that his lines show a direction (see figure 4). When he draws the lines he says “He (the captain) looks in this direction...”
Like the spots before, we think that Maura and Lukas give the lines as examples of possible solutions. When the researcher asked these students about spots between those lines, these spots were also recognised as possible solutions. This means that the solutions of the students were in fact as general as the solution the designers had in mind, and that only their representation was different . Our interpretation is that students came up with their own representations because they did not know yet the mathematical concepts of ‘line’, ‘point’ and ‘region’. For someone with more mathematical knowledge, lines and regions are representations of an infinite set of points and therefore it is enough, to mark a region by drawing its borders.
The map is interpreted differently
The three towers are shown on the map as little black blocks. These blocks were meant as symbols by the designers, but the students interpreted them as if they represented the real measurements of the towers. The students interpreted, in other words, the picture not as a map, but as an aerial view. In Tasks 4 and 6, almost all students did so. Some of them were quite explicit about it, like Simone who explained that the lines should go “till the edge of the towers”. It can also be seen in the drawings that students made like Maura’s drawing of Figure 5.
From the perspective of the students, it is logical that the width of the towers has to be taken into account, as the width is of real importance also in the computer program. If, for example, one has found a spot with the binoculars , where the lighthouse is behind the church tower, the boat can still be moved a little to the side while the lighthouse remains hidden.
So, here also we see a difference between the perspective of the designers and the perspective of the students. What was only a symbol in the eyes of the designers, indicating a point on the map, was interpreted by the students as a picture of a tower, as seen from above.
A different idea about which aspects of reality should be taken into account
Another difference between the designers and the students is that they hold different views about which aspects of reality are important in order to solve the problems. In Task 7, for instance, it is said that Zilt sees a ‘big ship’ between the other two towers. The word ‘big’ was used by the designers only to make the story more exciting, but Maura draws the conclusion that the ship must be near the coast. She says: “Zilt sees it big and therefore it can't be far from the coast”. To defend her idea for her peer and the researcher, she brings up several aspects of reality: the weather conditions (“It can be foggy, and then one cannot see very far”), the scale of the map (“It is a small map, but actually it is very big”) and the fact that things that are far away look small. Her peer Silvana, however, shows that she has a different opinion. :
Maura: “He sees it big, the ship”.
Silvana: (to Maura) “yes, but that is just
... that belongs to the story. The task is ’where can the ship be?’”
Silvana shows here that she knows that in mathematics one doesn’t have to take all contextual elements into account. Some of the aspects just “belong to the story”. One could say that Maura and Silvana do not share the same socio-mathematical norms with respect to the question which aspects of reality should be taken into account.
The designers had not expected that describing the ship as a ‘big ship’ would influence the way a student would try to solve the problem. Like Silvana they had a different socio-mathematical norm in mind. We believe this has also to do with a different level of mathematical thinking. Designers look upon the task from a mathematical point of view, which makes them see lines and regions instead of the concrete situation.
Discussion
9In the previous section we have analyzed the teaching experiment in order to offer a detailed elaboration of what constitutes the actor's and the observer's point of view with a concrete example. In this section, we will expand on this elaboration, by analyzing the observed differences from a more theoretical perspective.
We may summarize the differences between the designers’ expectations and the ways students reasoned as follows. The designers did not anticipate that students would not think of ‘seeing’ as ‘looking-around-and-seeing’ but as seeing without moving your head. They expected students to think of lines and regions to construct their answers, while students felt the need to use different representations, drawing points (dots or crosses) on the line segments, and drawing series of lines and points to indicate regions. Finally, the designers and the students had very different ideas about the meaning of the symbols for the towers on the map, as well as about which aspects of reality are to be taken into account.
To analyze these differences from the perspective of an actor’s and an observer’s point of view one has to look at what both parties bring to the situation. We found that the following differences in the backgrounds of designers and the student play a significant role: a difference in the level of mathematical thinking, a difference in beliefs about what aspects of reality should be taken into account, and a difference in mathematical (or non-mathematical) attitude. We will elucidate this in the following.
Differences in level of mathematical thinking
Instructional designers and students may both use mathematical terms as ‘point’ and ‘line’. But—according to the Van Hiele (1973) theory—these words may have different meanings for both parties. Applied to points and lines, the Van Hiele theory suggests that, for students, points and lines are things with a certain size and shape, which you can see and draw, while they are mathematical objects for the instructional designers. Following Van Hiele, we may speak of two different levels of thinking. On a ground level points and lines are visual entities, but on the next level points and lines have become mathematical objects. Or, to use Van Hiele’s terminology, they have become junctions in a network of mathematical relations. Points and lines have become thought objects that differ significantly from their material counterparts. Mathematical points are infinitesimally small, and a line is defined as a set that consists of an infinite number of such points.
The notion of a line as a set of points, plays a distinctive role in the way one answers some of the tasks. Take task number 4, for instance. This task requires the students to find out where the captain would see only two of the three towers. With the idea of a line as a set of points in the back of your mind it seems self evident to choose line segments as solutions to this question. Without this mathematical notion it is much more natural to look for or represent individual points.
Differences in taking aspects of reality into account
The students appeared much more inclined to take various aspects of reality into account than the designers had anticipated. We may assume that the instructional designers were guided by the mathematics they could ‘see’ in the tasks, when considering which contextual elements are important for the problem. At the same time, they may have be unaware of the extent to which the mathematical content of the task differs from the real-life context. Students, however, are often very sensitive to such differences. They may focus on the context, and look for those contextual elements that can help them to make sense of what is asked of them. In this process of grasping the problem, they use their life experience creating a context for that activity. Or, as Mercer (1992, p. 31-32) puts it:
“Pupils accomplish educational activities by using what they know to make sense of what they are asked to do. As best they can they create a meaningful context for an activity, and the contexts they create consist of whatever knowledge they invoke to make sense of the task situation.”
The context and knowledge about the real world played a central role in the solution processes of the students. We may explain this from their lack of familiarity with the mathematics, but we can also relate this to the socio-mathematical norms (Cobb & Yackel, 1995) to which the students were accustomed. The extent to which the context must be taken into account when solving a contextual problem in a certain classroom, is a typical part of the socio-mathematical norms of that classroom. So the fact that the students incorporated aspects of reality on a larger scale than the designers expected, might also be explained by socio-mathematical norms of the classroom. The students may have acted in accordance with what they perceived as what the norms in their classroom were in regard to dealing with aspects of reality. It might, however, also be the case that the students experienced the classroom social norms and socio-mathematical norms as situated (Lave & Wenger, 1991). The computer activities might have constituted a different situation for them, where the norms of the classroom did not apply.
Mathematical attitude
A third difference between the students and the designers may reside in the mathematical attitude. In reflection on the above, we may observe that the influence of differences in level of mathematical thinking merges with the influence of socio-mathematical norms. The socio-mathematical norms delineate how and in how far elements of the context are to be taken into account. The way, in which elements of the context actually are taken into account, however, will not be solely defined by socio-mathematical norms, but will also be influenced by the level of mathematical thinking. One cannot expect students to come up with solutions that correspond with mathematical ideas they have not yet acquired. In addition to this, we should note that the measure in which one has a mathematical attitude will play a role too.
Krutetskii (1976) found that mathematically gifted students tended to solve problems by generalizing the problem, solve the problem on this general level, and finally translate this solution back to the specific problem at hand. In a similar sense, mathematically disposed persons such as instructional designers may be inclined to look for more general solutions, without even being aware of it.This mathematical attitude may also explain the difference in interpretation of the map; as the designers may have developed a habit of ‘decontextualizing’ contextual problems as part of a mathematical attitude. Consequently, when they look at the map, they see a mathematical model of the situation, and not like students, a picture or an aerial photograph of the island. The designers considered the symbols of the towers on the map as points, while students interpreted those symbols as top views of the towers.
Instructional design recommendations
We close this discussion with some remarks on what measures might be taken to improve the computer game. We start by noting that the observed consequences of the differences between the observer’s and the actor’s points of view, caution instructional designers to consider the contextual situation of the tasks carefully, and not underestimate the differences between a real world interpretation of a contextual problem and a mathematical interpretation of that problem. As a rule, one should try to look at the tasks' context from the point of view of the students. Further, it seems essential to include in the designing process small teaching experiments that aim at coming to understand the students' point of view.
We saw that the students eventually came to see line segments as legitimate solutions, as a result of the interaction with the researcher. So we may ask ourselves whether it would be possible to adapt the computer program in such a manner that it would support this kind of shift. If we take the task to be on the position from where the captain will only see two towers, the program might, for instance, first ask for one position, then five, and finally ask for all possibilities.
In regard to the interpretation of the map of the island, a recommendation would be to make the difference between the reality and the model more explicit. One of the problems of the tasks had to do with the fact that the instructional designers ‘see’ the map as a model of the reality, while students see it as a realistic picture. The step from the reality to the model could be made more explicitly by working with two representations, a realistic top view of the island, and a schematic picture of the island on which the towers are represented with points.
The idea of looking around could also be made more explicit in the text of the tasks, and supported by binoculars which students can change the direction of, and so actually look around.In relation to this, we would suggest to enhance the context of the problem by constructing a reason why one might want to find an answer to a given question. This reason then might guide the way in which the students think about the problem.
Finally we turn to the social norms, the socio-mathematical norms, and mathematical attitude. Classroom norms are constructed on the basis of experiences, in an interactive and accumulative process, which is guided by the classroom teacher. We argued that an educational computer game constitutes a situation that may be experienced as quite different from the classroom, in which different norms apply. In order to prepare the students for inquiry-based computer tasks, the classroom teacher will have to establish inquiry-orientated classroom social norms, and appropriate socio-mathematical norms. Moreover, the teacher needs to try to cultivate a mathematical attitude. Still, students may disregard those norms when interacting with the computer environment. We doubt whether it would be possible to shape the computer program in such a manner that it can effectively influence the beliefs of the students in this respect. Maybe some well-designed tasks, and some tailored feedback may have some influence, but, considering the complexity of this learning process, the limitations of computer learning environments, and the richness of possible student reactions, we believe that there will always be an essential role for the teacher to interact with the students who work on educational computer games in mathematics.
References
10Doerr, H.M. & R. Zangor (2000). Creating Meaning for and with the Graphing Calculator. Educational Studies in Mathematics, 41, 143-163.
Gravemeijer, K.P.E. (2002). Preamble: From models to modeling. In: K. Gravemeijer R. Lehrer, B. van Oers & L. Verschaffel (eds.). Symbolizing, Modeling and Tool Use in Mathematics Education. Dordrecht: Kluwer Academic Publishers, 7-22.
Hiebert, J., Carpenter, T.P., Fennema, E., Fuson, K., Wearne, D., Murray, H., Olivier, A. and Human, P. (1997). Making Sense: Teaching and Learning Mathematics with Understanding. Heinemann, Portsmouth, NH.
Footnotes
11[1] Treasure Island was designed by Frans van Galen. The illustrations here are taken from the English translation. The applet can be found at http://www.fi.uu.nl/toepassingen/00032/en/eiland1.html (English) or http://www.fi.uu.nl/toepassingen/00032/nieuwst/eiland1.html (Dutch).
[2] The English translations of these tasks can be found at http://www.fi.uu.nl/toepassingen/00032/islandstudy/en/ (English) or http://www.fi.uu.nl/toepassingen/00032/islandstudy/nl/ (Dutch)
About the Authors
12Nisa Figueiredo is a staff member of the Freudenthal’s Institute with experience in curriculum development and research in mathematics at the primary school level. Her research interests include longitudinal teaching-learning trajectories, professional development of primary school teachers and mathematics education for children with Special Needs.
Frans van Galen is a senior curriculum developer at the Freudenthal institute. He has a wide range of expertise in the area of mathematics education and the use of computers. He has been author of an RME textbook series for Dutch primary schools, and was involved in the development of the textbook series for the American Middle School "Mathematics in Contexts". He is a key designer for many of the Institute's educational applets and a developer of interactive content for educational publishers.
Koeno Gravemeijer is professor in Science and Technology Education at Eindhoven University of Technology. Earlier he was professor in Mathematics Education at Utrecht University and Vanderbilt University. His research interests concern curriculum development, instructional design, domain-specific instruction theories (such as the theory for realistic mathematics education, RME), teacher professional development, and students’ use of symbols and modeling. In relation to the latter he developed the so-called ‘emergent modeling’ design heuristic. He has been the main author of an RME textbook series for Dutch primary schools, and was also involved in the development of the textbook series for the American Middle School "Mathematics in Contexts". He directed a national project that elaborated learning routes and attainment targets in primary school for rational numbers, and measurement & geometry in 6th, 7th, and 8th Grade. He was also the coordinator of a cluster of research projects on mathematics and information technology.