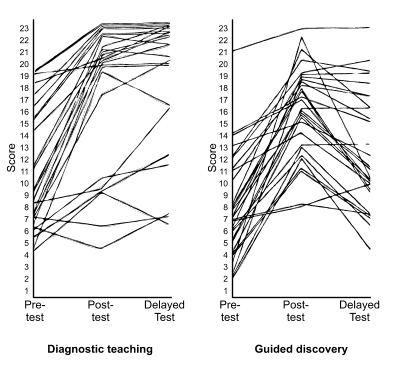
To give just one example, the study on reflections (Birks 1987) compared the effectiveness of the diagnostic approach with a popular guided-discovery textbook approach. Both methods involved ‘predict and check’ activities, which might lead to cognitive conflict. The main difference between the methods, however, was in the emphasis laid down in the diagnostic teaching lessons on making intuitive methods and common errors explicit, encouraging students to articulate theories and challenging ideas produced by other groups. In the ‘guided-discovery’ lessons, students worked individually with little discussion and debate. Students in both groups took the same pre-, post- and delayed post-tests (10 weeks after the experiment had finished), using items drawn from the CSMS research study (Hart et al. 1985). The results revealed that both groups made similar learning gains during the lessons, but the “conflict + discussion” approach was significantly more effective for longer-term learning (see Figure 1).


Lesson Design for Formative Assessment
Malcolm Swan & Hugh Burkhardt
Shell Centre for Mathematical Education
University of Nottingham, England
Summary
1The potential power of formative assessment to enhance student learning is clear from research. This, however, demands a different learning culture and a broader range of teaching approaches than are found in most mathematics classrooms. Earlier efforts to introduce formative assessment for learning have focused on teacher professional development. Here we describe a major project that explores how this change may be stimulated and supported by teaching materials that embody the principles of formative assessment. We describe the design challenges we faced, the previous research and development experience we drew upon, and the principles that directed our designs. We illustrate these elements with examples of the products themselves, some outcomes and lessons learned.
Introduction
2The potential power of formative assessment for enhancing learning in mathematics classrooms was brought to widespread attention by the research review of Paul Black and Dylan Wiliam (1998) and subsequent publications (Black et al. 2003; Black et al. 1999). This work was brought together in a practical guide by Wiliam and Thompson (2007), while Black and Wiliam ( 2009, 2014) have developed further the theoretical aspects of formative assessment.
They and others launched programs of work that aimed to turn these insights into impact on practice, mainly focusing on the professional development of teachers. They found, however, that regular meetings over a period of years were needed to enable a substantial proportion of teachers to acquire and deploy the “adaptive expertise” (Hatano & Inagaki 1986; Swan 2006a) needed for self-directed formative assessment. This is clearly an approach that is difficult to implement on a large scale. Since Black and Wiliam’s research was published, the term “formative assessment” has entered teachers’ common language though it has often been corrupted to mean more frequent testing, scoring and record keeping[1]. Their original use of the term includes:
"… all those activities undertaken by teachers, and by their students in assessing themselves, which provide information to be used as feedback to modify the teaching and learning activities in which they are engaged. Such assessment becomes ‘formative assessment’ when the evidence is actually used to adapt the teaching work to meet the needs.” (Black & Wiliam, 1998, para, 91)
Here lies the real challenge: for assessment to be formative the teacher must develop expertise in becoming aware of and adapting to the specific learning needs of students, both in planning lessons and moment-by-moment in the classroom.
In 2009, the Bill & Melinda Gates Foundation approached us to develop a suite of formative assessment lessons to form a key element in the Foundation’s ambitious program for “College and Career Ready Mathematics” based on the Common Core State Standards for Mathematics[3] (NGA & CCSSO 2010). In response, the Mathematics Assessment Project (MAP)[2] was designed to explore how far well-designed teaching materials can enable teachers to make high-quality formative assessment an integral part of the implemented curriculum in their classrooms, even where linked professional development support is limited or non-existent. The design challenge was recognized as formidable, since formative assessment involves a much wider range of teaching strategies and skills than traditional mathematics curricula demand. The research-based design of these lessons, now called Classroom Challenges, forms the core of this paper. The lessons are proving popular with teachers across the US[4]. Research into their impact on teaching and learning, in particular on the developing expertise of teachers who use them, is ongoing and will be reported in future publications. In this article we describe the design challenge we faced, some of the previous research and design experience we drew upon, the principles that directed our designs, along with examples of the products themselves.
Design challenges
3Turning the principles of formative assessment into effective lesson materials based on the Common Core State Standards for Mathematics (CCSSM) raised major design challenges. These include the design of lessons that explicitly foster mathematical concepts, problem solving strategies and “mathematical practices” – a key new feature of these standards. The writers of the Standards summarized their goals for student learning in an early draft as follows:
“Proficient students expect mathematics to make sense. They take an active stance in solving mathematical problems. When faced with a non-routine problem, they have the courage to plunge in and try something, and they have the procedural and conceptual tools to carry through. They are experimenters and inventors, and can adapt known strategies to new problems. They think strategically.”
The contrast of this picture with the pattern of activities in most current mathematics classrooms is striking; learning and reliably reproducing standard procedures for calculation in arithmetic and algebra is now no longer enough.
Developing mathematical concepts
Diagnostic tests often reveal profound misunderstandings of mathematical concepts. The usual responses are of two kinds. The teacher may accept as inevitable the wide variations in understanding among their students and continue with their original plan; this is clearly not formative assessment. Or, when the shortcomings are too blatant, they may rapidly reteach the concepts. That re-teaching is ineffective should not be a surprise – a student who misunderstood the first time is unlikely to do better when the same teaching is repeated at higher speed.
Research on learning mathematics (Dickson et al. 1984; Hart 1980; Ryan & Williams 2000) makes it clear that students’ conceptual difficulties are often caused by over-generalization, where students make connections between prior knowledge and new domains. For example, students often generalize from their experiences with natural numbers that “numbers with more digits are larger in value”, “multiplication makes things bigger”, or that “when multiplying by 10, you ‘add a zero’”. Such sensible generalizations become misconceptions when applied to the new domains of decimals and fractions. Similarly, standard restricted paradigmatic examples presented in textbooks lead students to generalize that “you always divide the larger number by the smaller” or “the larger the area, the greater the perimeter”.
The first challenge for the project was therefore to apply previous research into conceptual development (see below) by designing formative assessment lessons that uncover students’ existing ways of thinking, then create ‘cognitive conflicts’ or ‘disturbances’ that lead students to realize and confront inconsistencies. The lessons must then help to resolve these conflicts – in our design, through student-student and student-teacher discussion, in pairs or small groups, and then across the class as a whole.
Developing mathematical problem solving strategies
“Problem solving” is used with many different meanings. Here we use it in the sense that is now widely accepted in the international mathematics education community. A problem is a task that is:
- Non-routine: A substantial part of the challenge is in working out how to tackle the task. Sometimes, as in real life, problems may contain insufficient or superfluous information so that assumptions – and, usually, simplifications–have to be made.
- Mathematically rich: Substantial chains of reasoning, involving more than a few steps, are normally needed to solve a task that is worth calling a problem.
- Reasoning-focused: Answers are not enough; in problem solving, students are also expected to explain the reasoning that led to their solutions and why the result is true.
Problems of this type are rarely seen in mathematics classrooms. More normally, students are given ‘problems’ immediately after being taught the relevant content and method. They are thus, in effect, illustrative exercises in using the just-taught material. In the sense described here, however, problem solving involves recognizing and selecting, from your whole mathematical toolkit, tools appropriate for the problem. This in turn involves building and using connections with other contexts and with other parts of mathematics. Problems are therefore more difficult than a well-defined exercise involving similar mathematical content. So, for a problem to present a challenge that is comparable to a routine exercise it must be technically simpler, involving mathematics that was taught in earlier grades and has been well-absorbed by the student.
Problem solving in this sense presents new challenges to teachers. The dilemma is captured in a quote from a fine teacher, new to problem solving:
“I know I mustn’t tell them how to do it. But I can’t just stand there. What am I supposed to do?”
To tackle this, teachers need teaching materials that will provide effective support, complemented by whatever professional development may be available.
Developing mathematical practices
As well as setting out specific mathematical concepts and skills appropriate at each grade, the CCSSM emphasize the importance of students acquiring a range of practices that are involved in “doing mathematics”. These cross-cutting practices apply to both conceptual learning and problem solving. Eight mathematical practices are listed:
- Make sense of problems and persevere in solving them.
- Reason abstractly and quantitatively.
- Construct viable arguments and critique the reasoning of others.
- Model with mathematics.
- Use appropriate tools strategically.
- Attend to precision.
- Look for and make use of structure.
- Look for an express regularity in repeated reasoning. (NGA & CCSSO 2010; p.6-8)
Each is described in a long paragraph, but the authors stress that the practices, along with the concepts and skills in the content specifications, should be regarded as a coherent whole – not a set of separate elements to be taught (and tested) individually. The challenge for the project was therefore to design specific lessons that enable teachers and students to understand and develop these practices, illustrating and supporting the new pedagogies involved.
The strategic design and the products
4Strategic design (Burkhardt 2009) concerns those features of a product that relate the design to the roles it is to play in the system it is designed to serve – in this case, supporting the implementation of CCSSM in classrooms across the US. As noted above, the Common Core represents higher performance targets involving richer problems that are more complex, less routine, requiring longer chains of reasoning and greater student responsibility and autonomy. This in turn requires the design of learning activities that are less imitative and involve more discussion and reasoning, with new roles for students and new skills for teachers. Substantial professional development support could not be assumed; even where this resource was available, it was unlikely that the leaders would be experienced in formative assessment.
The Bill & Melinda Gates Foundation saw formative assessment lessons in mathematics, built on the Shell Centre’s prior work, as playing a central role in their “College and Career Readiness” strategy.
“Our focus is on ensuring that all students — regardless of skin color or zip code — graduate from high school ready to succeed in college, career and life. So we built our college-ready program on several core initiatives:
- Ensuring that students are prepared for college and careers (learning)
- Empowering effective teachers and making sure that every student has a highly effective teacher in every class, every day (teaching)
- Promoting innovation in the classroom and developing next-generation school models (innovation) and,
- Establishing a culture of data and evidence to ensure that truly effective innovations for students and teachers are the ones we promote.
In each of those areas, we’re looking for the levers, the intervention points, within the education system where an investment can yield new insights and scalable solutions.”
(Vicki Phillips, Director of Education, Bill & Melinda Gates Foundation, 2010)
The Shell Centre also pointed out the key role that high-stakes summative assessment plays in determining what actually happens in classrooms. The Foundation agreed to fund some development of tasks and tests but were understandably cautious about getting too involved in the controversial issues of high-stakes testing. Their working assumption is that, since two inter-state consortia have been funded by the US Government to develop tests that assess the aims embodied in CCSSM, the tests that emerge will really do so[5].
These strategic needs led us to design the following range of products[6].
(i) Formative assessment lessons
The challenges presented to teachers by CCSSM made clear the need for lesson materials that epitomize the Common Core, emphasizing the mathematical practices and other features that receive little or no attention in most published curricula. Rather than compete directly with such curricula, it was decided to develop supplementary materials, covering 10-15% of teaching time, which would address the new challenges that CCSSM presents. Given the potential of formative assessment, it was agreed that we should develop formative assessment lessons of two kinds, focused on the design challenges outlined in Section 2 above: Concept development lessons focused on specific concepts and skills, as set out in the content standards, and Problem solving lessons. Both types of lesson would be infused with the development of the mathematical practices. The name “Classroom Challenges” was chosen, reflecting both the deeper probing and the length of the lessons, typically a short preliminary assessment and a main lesson taking two class periods.
The design of each of these lessons is the main theme of this article. However, we should mention two other kinds of products that complement the lessons in supporting the strategic design: professional development modules; and tasks and tests for summative assessment.
(ii) Professional development modules
It was recognized that, while the lessons themselves give teachers a great deal of support in developing the adaptive expertise and subject knowledge that CCSSM demand, there is a need for further professional development support, focused on more general issues of pedagogy and mathematics. Issues of scale, and the limited number of leaders who are expert in formative assessment, suggested a need for materials that directly support these aspects of professional development. These modules have been designed to fill this need. Each is focused on a specific aspect of expertise, namely:
- Formative assessment: How can I respond to students in ways that improve their learning?
- Concept development: How can I help students develop a deeper understanding of Mathematics?
- Problem solving: Do I stand back and watch, or intervene and tell them what to do?
- Improving learning through questioning: How can we ask questions that improve thinking and reasoning?
- Students working collaboratively: How can students learn from discussing mathematics?
The approach to professional development is “activity-based”, building teachers’ professional expertise through guided structured discussion of key issues. It stays close to the classroom: each module involves collective preparation of a lesson, which the participants then teach in their own classrooms, returning for structured reflection on what happened and its implications. The professional development modules provide handouts and guidance notes for teachers and session leaders, supplied in pdf form for printing or on-screen use. They make use of video, showing real teachers trying new material with their classes and discussing the issues with colleagues. The modules are designed to be used by teachers with a professional development leader.
(iii) Tasks and tests for summative assessment
These are designed to fill two complementary purposes:
- to give teachers tools for the summative assessments that their school and district continue to require them to perform – but tools that are balanced in terms of the CCSSM;
- to offer high quality exemplars to those responsible for commissioning high-stakes tests, and those responsible for designing them.
These products are now being used in the professional development of district advisors and test writers.
The lesson design principles
5Research-based lesson design and development has three essential elements: input from prior research; creative design ideas; and systematic development through successive rounds of trialing. We will next discuss the first and last of these elements, while the remainder of the article will deal with the design aspects. Creative design is essential if we are to transform students’ mathematical experience from passive and imitative[7] into active and autonomous. Systematic development is essential in making sure the design works as intended for typical users, both teachers and students.
Prior research
The Shell Centre team has an established track record for designing materials that, with careful development through iterative classroom trials in increasingly realistic circumstances, enable teachers to achieve the expertise that is needed in challenging areas of improvement. Inspired by the Black-Wiliam work, we asked ourselves how far well-engineered teaching materials could enable teachers to make formative assessment part of their teaching. We recognized that we had much to build on. The Shell Centre’s “Diagnostic Teaching” program of design research in the 1980s was an example of formative assessment of the kind identified as effective by Black and Wiliam (See e.g. Bell 1993; Swan 2006a).
The main phases of a typical diagnostic lesson are outlined in Table 1. This approach to teaching mathematical concepts proved to be more effective, over the longer term, than either expository or guided discovery approaches. This result was replicated over many different topics, and with different designers: decimal place value, rates, geometric reflections, functions and graphs, and fractions (Bassford 1988; Birks 1987; Brekke 1987; Onslow 1986; Swan 1983). From these studies it was deduced that the advantage of diagnostic teaching appeared to lie in the extent to which it valued the intuitive methods and ideas that students brought to each lesson, offered experiences that created inter- and intra-personal ‘conflicts’ of ideas, and created opportunities for students to reflect on and examine inconsistencies in their interpretations. A phase of ‘preparing the ground’ was found necessary, where pre-existing conceptual structures were identified and examined by students for viability. The ‘resolution’ phase involved students in intensive, reflective discussions. Indications were that the greater the intensity of the discussion, the greater was the impact on learning.
Table 1: Phases in a diagnostic teaching lesson (Swan 2006a)Before teaching, explore existing conceptual frameworks through tests and interviews.
Students’ intuitive interpretations or methods are identified through written tests and possibly follow-up clinical interviews.
Make existing concepts and methods explicit in the classroom
An initial activity is designed with the purpose of making students aware of their own intuitive interpretations and methods. At the beginning of a lesson, for example, students are asked to attempt a task individually, with no help from the teacher. No attempt is made, at this stage, to ‘teach’ anything new or even make students aware that errors have been made. The purpose here is expose pre-existing ways of thinking.
Provoke and share ‘cognitive conflicts’
Feedback to the students is given in one of three ways:
- by asking students to compare their responses with those made by other students;
- by asking students to repeat the task using alternative methods;
- by using tasks which contain some form of built-in check.
This feedback produces ‘cognitive conflict’ when students begin to realize and confront the inconsistencies in their own interpretations and methods. Time is spent reflecting on and discussing the nature of this conflict. Students are asked to write down the inconsistencies and possible causes of error. This typically involves both small group and whole class discussion.
Resolve conflict through discussion and formulate new concepts and methods.
A whole class discussion is held in order to ‘resolve’ a conflict. Students are encouraged to articulate conflicting points of view and reformulate ideas. At this point, the teacher suggests, with reasons, a ‘mathematicians’ viewpoint.
Consolidate learning by using the new concepts and methods on further problems.
New learning is utilized and consolidated by
- offering further practice questions
- inviting students to create and solve their own problems within given constraints;
- asking students to analyze completed work and to diagnose causes of errors for themselves.
In these early studies, the teaching was usually conducted over a short period by the researchers themselves, or by volunteer teachers who were particularly interested in exploring new teaching approaches. Subsequently, further research was carried out in more typical contexts and over longer periods. In 1995, a funded study into diagnostic teaching in Further Education (FE) colleges showed that collaborative discussion materials can be effective when used appropriately, even with low attaining students (Swan 2000). It also offered insights into the ways in which teachers’ beliefs (about mathematics, teaching and learning) affect the ways in which they use teaching materials and, conversely, the ways in which the materials affect beliefs and practices.
At this point, it was recognised that, for large-scale impact to be achievable, the research focus had to move from student learning towards replicable models that include teachers’ professional development (PD). The emergent design principles were based on teachers learning “constructively” from structured reflection on a sequence of carefully planned teaching experiences in their own classrooms.
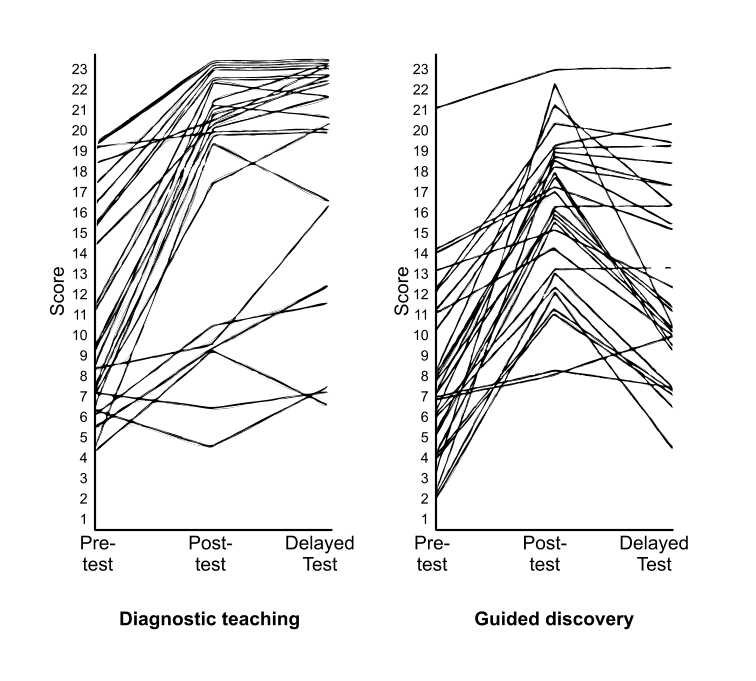
| Mean scores (%) | Mean gains (%) | ||||
|---|---|---|---|---|---|
| Pre | Post | Delayed | Pre-post | Post-delayed | |
| Guided-discovery (n=29) | 32.5 | 69.9 | 53.7 | +37.4** | -16.2* |
| S.D. | 18.5 | 16.8 | 21.1 | ||
| Diagnostic teaching (n=26) | 48.5 | 78.6 | 81.8 | +30.1** | +3.2** |
| S.D. | 24.4 | 26.4 | 24.0 | (*p<0.05, **p<0.01, 2-tailed T) | |
The UK government then funded the development of a multimedia professional development resource to support diagnostic teaching of algebra (Swan & Green 2002). This was distributed to all FE colleges, leading to research on the effects of implementing this collaborative approach to learning in 40 “retake” classes, involving 17-year old students who had not succeeded in the GCSE examination the previous year. This again showed the greater effectiveness of approaches that encourage misconceptions in algebra to be elicited and directly addressed through student-student and whole class discussion (Swan 2006a, 2006b; Swan 2006c). The government, recognizing the potential of such resources, commissioned the design of a more substantial multimedia PD resource, ‘Improving Learning in Mathematics’ (DfES 2005). This material was trialled in 90 colleges, before being distributed to all English FE colleges and secondary schools. An adaptation was sent to all adult education lecturers (NRDC 2006).
The research on formative assessment covers a variety of studies and approaches, some much more effective than others. The review by Black and Wiliam identified those features that characterized the studies that shown substantial student gains. Some of these were, at first, surprising. For example, the research showed clearly that giving scores to students on an assessment destroys its formative potential for helping them improve their reasoning. Scores distract students from the work, instead encouraging them to compete with peers. Once they have a score, students pay little or no attention to any other guidance the teacher may provide. Our subsequent interviews with students have confirmed this. Thus in the design of these lessons, we encourage teachers to look for misunderstandings that many students show, basing their formative guidance on these and avoiding individual scores[8].
All this work underlines the need to change the set of mutual expectations, “who will do what”, of teachers and students in the classroom – the didactic contract of Brousseau (1997). Another strand of early Shell Centre research also illustrated the power that materials alone can have in this. It focused on the roles that teachers and students play, and that role-shifting raises the level of classroom discourse in both content and sophistication. This study of 170 lessons (Burkhardt et al., 1988) compared mathematics teaching from a standard textbook with investigative lessons using interactive microworlds – with one computer screen for the class. Teacher and student dialogue was captured in real time using a systematic classroom analysis notation, SCAN (Beeby et al. 1980). Analysis showed, unsurprisingly, that in normal mathematics lessons, teachers play directive roles, classified as: manager, explainer and task-setter. In contrast, when using the investigative materials, the teachers largely left these roles to the students and the software while they moved naturally into facilitative roles: counselor, fellow-student, and resource. While the computer, too, played an important role, effectively acting as a teaching assistant, it was encouraging that this dramatic shift in classroom roles could be achieved with minimal professional development – the challenge we faced here.
The design process: development at a distance
The Shell Centre’s methodology for developing materials, complements input from prior research and imaginative design with rich and detailed feedback from small-scale classroom trials. The objective of these is to give the design team a detailed picture of what happened in the use of their trial materials by teachers to guide revision. The aim is to learn more about questions including:
- Do the teacher and students understand the materials?
- How closely does the teacher follow the lesson plan?
- Are any of the variations damaging to the purpose of the lesson?[9]
- What features of the lesson proved awkward for the teacher or the students?
- What unanticipated opportunities arose that might be included on revision?
This approach, though standard in product development generally, is much more expensive than the “authorship model” so often used in education: produce a draft; gather comments; revise; publish. In our work, we observe each lesson between three and five times at each of two cycles of development. This sample size enables us to obtain rich, detailed feedback, while also allowing us to distinguish general implementation issues from more idiosyncratic variations by individual teachers.
For developments in the UK, the design team members play an important role in the early stages of the observation process, trying lessons themselves and/or observing another teacher; for this project, there were only rare opportunities for the designers to observe the lessons in the US classrooms for which we were designing. We were thus entirely dependent on our US observers for this essential feedback. We were fortunate to have three groups of people with deep understanding of classrooms in California, Rhode Island and the Midwest.
In order for feedback to be useful in the revision process it has to be specific and reliable, based on a detailed description of what occurred in the lesson. Experienced lesson observers are accustomed to making holistic judgments for professional development guidance. They tend to find detailed description difficult, even uncongenial, offering instead suggestions for revision without detailing the evidence on which they are based. Such suggestions may be wise or they may be based on a misunderstanding of features of the design that are not obvious to the observer. In contrast, others with less experience (typically graduate students) are good at detached observation and description but lack the deeper insights that experienced lesson observers may bring.
To meet this challenge, a detailed protocol was developed through several versions. This process, epitomizing challenges faced by all design teams, is of wider interest. In Figure 2Figure 2 we show the current version of the protocol, which has been the instrument for communication between by the observers and the design team for most of this project. Two core design questions permeate the protocol: How well do the materials communicate to the teacher and students the intentions of the designer? How far was the learning experience profitable for students?
Part 1 of the protocol is purely descriptive. We sought to capture something of the lesson context, the nature of the students, the environment, and the support given to the teacher beforehand. Then there is a request for a vivid description of the course of events, coupled with a sample of six pieces of student work of varied quality. Significant events that might inform the designer were noted.
Part 2 is analytical. Observers were asked for: their overall impressions; deviations from the lesson plan; quality of teacher questioning; quality of student reasoning, explanations, discussion and written work. They were also asked to provide evidence of learning. They were specifically asked about the relevance of the formative assessment opportunities.
Part 3 sought the teacher’s views, from an interview after the lesson. Teachers were asked about their lesson preparation, their views on the lesson plan, the lesson and the response of students, and implications for professional development.
Over the course of the project, in the course of developing 100 Classroom Challenges, about 700 such reports have been constructed by the observers and analysed by the design team.
 Open as PDF
(10 pages) (The full
PDF can be viewed online.)
Open as PDF
(10 pages) (The full
PDF can be viewed online.)
Design principles and tactics
The design of these lessons built on a set of principles for effective teaching developed through international research on teaching and learning and, as we have seen, on our own Diagnostic Teaching program. A synthesis of principles was drawn up as part of a national consultation in the UK (Swan 2014). These are summarized in Table 2.
| Teaching is more effective when it ... | |
|---|---|
|
This means developing formative assessment techniques and adapting our teaching to accommodate individual learning needs. |
|
Learning activities should expose current thinking, create ‘tensions’ by confronting learners with inconsistencies and surprises, and allow opportunities for their resolution through discussion. |
|
Questioning is more effective when it promotes explanation, application and synthesis rather than mere recall. |
|
Collaborative group work is more effective after learners have been given an opportunity for individual reflection. Activities are more effective when they encourage critical, constructive discussion, rather than either argument or uncritical acceptance. Shared goals and group accountability are important. |
|
Learners often find it difficult to generalise and transfer their learning to other topics and contexts. Related concepts (such as division, fraction and ratio) remain unconnected. Effective teachers build bridges between ideas. |
|
Often, learners are more concerned with what they have ‘done’ than with what they have learned. It is better to aim for depth than for superficial ‘coverage’, even though this takes time. |
|
The tasks we use should be accessible, extendable, encourage decision-making, promote discussion, encourage creativity, encourage ‘what if’ and ‘what if not?’ questions. |
|
Effective teaching challenges learners and has high expectations of them. It does not seek to 'smooth the path' but creates realistic obstacles to be overcome. Confidence, persistence and learning are not attained through repeating successes, but by productive struggle with difficulties. |
|
Mathematics is a language that enables us to describe and model situations, think logically, frame and sustain arguments and communicate ideas with precision. Learners do not know mathematics until they can 'speak' it. Effective teaching therefore focuses on the communicative aspects of mathematics by developing oral and written mathematical language. |
|
What is to be learned cannot always be stated prior to the learning experience. After a learning event, however, it is important to reflect on the learning that has taken place, making this as explicit and memorable as possible. Effective teachers will also reflect on the ways in which learning has taken place, so that learners develop their own capacity to learn. |
|
ICT offers new ways to engage with mathematics. At its best it is dynamic and visual: relationships become more tangible. ICT can provide feedback on actions and enhance interactivity and learner autonomy. Through its connectivity, ICT offers the means to access and share resources and - even more powerfully - the means by which learners can share their ideas within and across classrooms. |
Table 2. Principles for the effective teaching of mathematics.
These principles are strongly reflected in the CCSSM. We will briefly mention a few of the many design tactics that, in building lessons from them, we have adopted to meet specific challenges that teachers face. Each of these was developed using feedback from observations of teachers in the classroom trials:
- Reflecting on and responding to student thinking
In “the heat of the classroom”, teachers often find it difficult to spend time listening and responding helpfully to student explanations. Interventions thus tend to be brief, superficial, directive and answer-focused, rather than reasoning-oriented. This is particularly the case when students are tackling problems that involve longer chains of reasoning. To assist in helping the teachers to prepare their interventions for each lesson, we suggest that they allow students an opportunity in advance of the main lesson to tackle an appropriate assessment, individually and unaided. The teacher then has time to review their work, anticipate and reflect on the approaches that are likely to be useful during the lesson, and prepare suitable interventions. - Giving formative, qualitative feedback to students
Given the clear result from the research on formative assessment, showing the destructive effect of scoring, how can we ensure they attend to the constructive guidance the teacher offers? In each lesson, we use our trial data and prior research to help the teacher anticipate likely difficulties and misconceptions that might arise (“common issues”) and suggest specific, appropriate, qualitative feedback that might be helpful for students, related to each issue. - Providing support to students without taking over
Teachers using thought-provoking questions, rather than explanations or direct instruction, is key; we suggest questions linked to each common issue and also suggest key questions at significant points in the lesson plan that will encourage students to think more deeply. - Adapting teaching to students with a range of difficulties
We use collaborative activities that encourage student self- and peer-assessment. This gives students a more responsible role, lightening the load on the teacher and building the students’ sense of responsibility for their own work. It requires the creation of tasks that may be shared, and we thus make extensive use of shared resources and group-generated products, such as posters. We do not offer students different tasks related to some pre-determined notion of ‘ability’ (“differentiation by prejudice”) but rather offer all students the same task and then, as needs emerge, extension challenges or additional support as necessary (“differentiation by outcome”). - Allowing students autonomy, yet confronting them with powerful methods
We know that students will tackle our tasks in many different ways, and we seek to encourage this. Yet we also realize that many students will adopt inefficient or unproductive methods and are unlikely to choose to deploy mathematical concepts and methods with which they are not fully comfortable. This leads to the familiar dilemma: How can we point out these shortcomings and demonstrate more powerful methods without the activity becoming an imitative exercise? The tactic we often use, particularly in problem solving lessons, is to present students with some handwritten sample work ‘from another class’. This is used to confront them, after they have tackled the problem for themselves, with some alternative approaches. Their task then typically becomes: (i) critique this sample work, correcting any errors; (ii) complete the approach to solve the problem; (iii) compare this approach with your own and try to evaluate its strengths and weaknesses. This approach moves the students into a new, critical role, thus increasing the metacognitive demand of the lesson[10].
In the following sections we describe in some detail how these principles manifest themselves in the design of concept development lessons and, rather differently, in formative assessment of problem solving.
The design of the Classroom Challenges
6We have sketched the development process and the design of the feedback that informs the revision and the refinement of the materials. We now illustrate how these design principles are embedded using two Classroom Challenges, both aimed at the Standards for Grade 7. The first is a concept development lesson on the topic of percentage increase, the second a problem-solving lesson, “Counting Trees”. The lessons may be downloaded from http://map.mathshell.org/materials/lessons.php.
A concept development lesson
Concept lessons are concerned with developing students’ ‘understanding’ of mathematical ideas. People tend to feel they have understood something when they achieve a sense of order and harmony, where there is a sense of a ‘unifying thought’, of simplification, of seeing some underlying structure and that in some sense, feeling that the essence of an idea has been captured (Sierpinska 1994). In our lessons we try to ensure these mental processes occur naturally, by making extensive use of lesson ‘genres’ (Swan 2008). The lesson we illustrate below is called “Increasing and Decreasing Quantities by a Percent” and is typical of the genre: “Interpreting multiple representations”. It is intended to be used about two-thirds of the way through a unit on teaching percentages. This allows teachers time afterwards to continue to build on the “diagnosis” and initial formative response that the assessment lesson provides. While the content of the lesson may be considered elementary, the structural links that are drawn in this design are not commonly made. These lessons are also useful later for review – we have found that many students, years after they are first taught percentages, struggle with this lesson. As their name implies, Classroom Challenges are designed to probe the concepts more deeply, “stress testing” their understanding.
1. Pre assessment.
 Click to enlarge
Open as PDF
(2 pages)
Click to enlarge
Open as PDF
(2 pages)
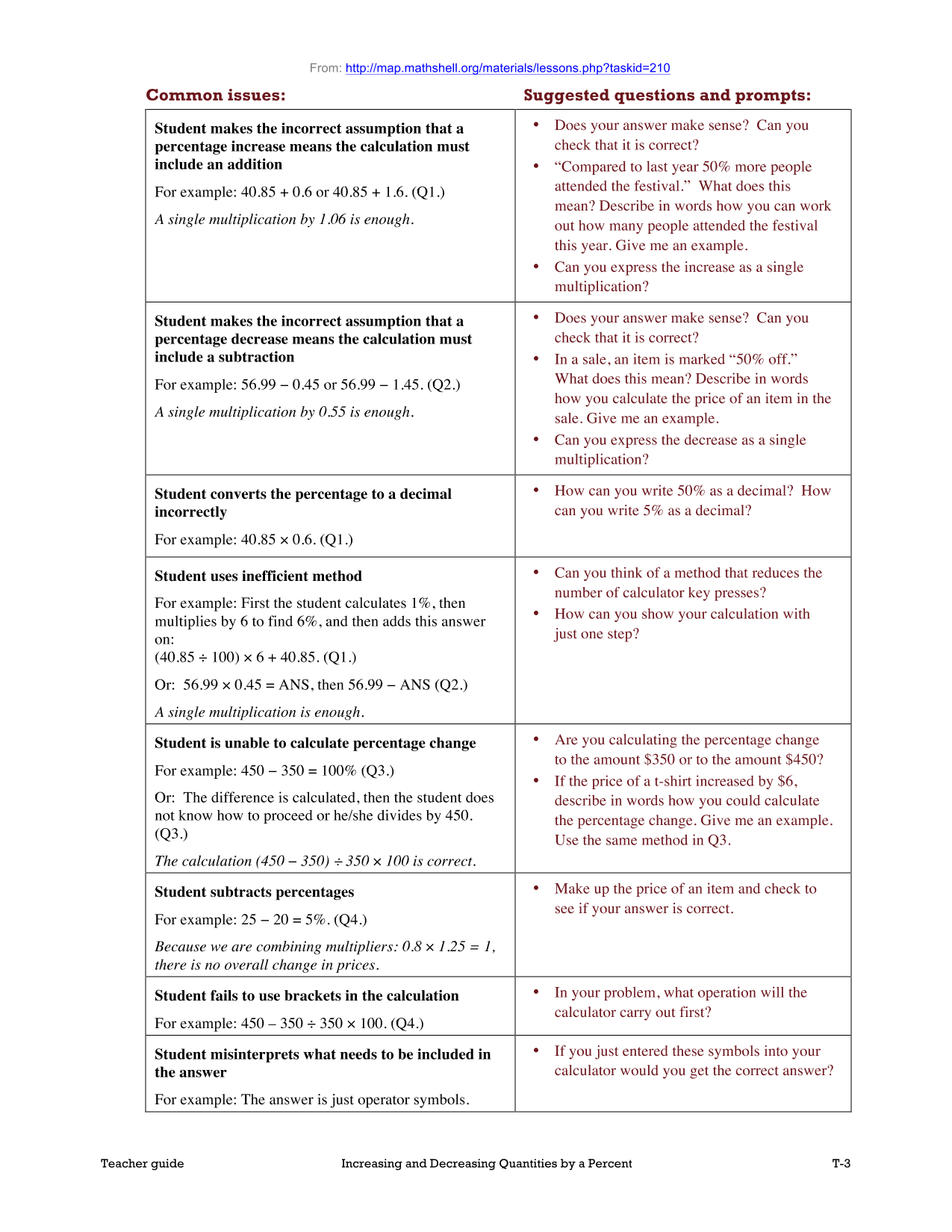
During a preliminary lesson, students are invited to tackle an assessment individually. In concept lessons, it consists of a carefully designed diagnostic sequence of a few tasks, taking a total of about 20 minutes. Students are not given help as they do this. The tasks are designed to expose common difficulties and errors. Students’ responses are collected by the teacher and analyzed, with the help of a table of common issues, provided in the teacher guidance along with associated questions that will help students move their reasoning forward (see Figure 3Figure 3). We recommend that the teacher write appropriate questions on each student’s work if time allows, or prepares a selection of questions for the whole class.
The complete teacher's guide can be downloaded from the online version of this article.
2. The formative assessment lesson.
The main lesson begins with a collaborative activity that is designed to reveal students’ existing ways of reasoning and to provoke cognitive conflict. The aim is to provoke dialogic talk (Alexander 2006, 2008; Mercer 1995, 2000) in which students, in pairs or small groups, assist one another to develop the target concepts.
Students are first given Money cards (representing 'states') and Percentage change cards ('changes'). Students are asked to position the money cards on the corners of their ‘poster’ as shown, then invited to take turns at choosing change “arrows” and placing these so that between two states there are appropriate changes, as in Figure 4. Typically, they make the mistake of pairing an increase of 50% with a decrease of 50%, and so on. (Notice that the design of the cards must permit this possibility.) Such errors are not commented on at this stage. This part is intended to expose misconceptions such as: n% increase followed by an n% decrease results in no change.
Groups are now issued with a set of 'decimal multiplier' cards to add to the existing arrangement, relating these both to the money cards and also to the percentage changes. Calculators are used to check that these are correctly positioned, thus giving immediate feedback. This provides conflict and discussion when students realize that their initial positioning of the percentage changes was incorrect. Finally, students are given fraction multiplier cards and are invited to add these to the table. A final complete, correct, arrangement is shown in Figure 5. The fractions are particularly powerful at providing opportunities for students to explain links between each percent change and its inverse. Throughout this complex process, students are encouraged to explain connections to one another and make generalizations.
Students that finish quickly are invited to find the percent changes and decimal multipliers that lie between the diagonals $100/$200 (as shown) and $150/$160, which is more challenging.
At each stage of this work, we suggest that one student from each group be invited to visit another group and ask them to explain their reasoning for the card placements they have made. In some classrooms students are asked to assemble posters, gluing down their cards, and present their findings to the rest of the class. This gives status to their ideas.
The lesson is concluded with a whole class discussion, where students discuss what they have learned. The teacher encourages students to extend and generalize their ideas by making small changes to the examples and by explicitly formulating general rules for equivalence. The teacher can, for example, suggest replacing the money cards with geometrical shapes. The teacher's role is thus to recognize and value the important contributions of students, and extend and 'institutionalize' them (Brousseau 1997). The teacher may ask, for example:
- Suppose prices increase by 10%. How can I say that as a decimal multiplication?
- How can I write that as a fraction multiplication?
- What is the fraction multiplication to get back to the original price?
- How can you write that as a decimal multiplication?
- How can you write that as a percentage?
Students may respond by writing answers on small whiteboards (an invaluable tool) and then holding them up for the teacher to see. This simple formative assessment strategy enables the teacher to assess everyone quite quickly and to follow up with further questions. At other stages in a lesson, these may also be used to respond to more open questions, such as “Show me an example of …”.
3. Post assessment.
At the end of the lesson, students’ responses from the initial assessment task are returned to them, along with the formative feedback questions and a second blank copy of the task. Students are instructed to review their original responses and consider their learning during the group activity, then try to improve their work. In addition, the teacher might provide some further questions of a similar type to assess learning.
A problem solving lesson
As we have noted, problem solving lessons are not primarily about developing understanding of mathematical ideas, but rather about students developing and comparing alternative mathematical approaches to non-routine tasks for which students have not been previously prepared. During the lesson there is therefore no formal teaching of mathematical ‘content’. The problems are designed with the aim of enabling the students to put together for themselves from their “mathematical toolkit” the mathematics useful for the problem, and to use it effectively. The challenge for students is to develop a mathematical formulation of the problem that incorporates the essentially relevant factors, represented in a suitable way, and to be aware of the assumptions they have made, and the effect these assumptions have on the solution.
The structure of a typical problem-solving lesson will be illustrated using the Classroom Challenge: Counting Trees (Figure 6).
1. Pre - assessment
In a preliminary assessment, as before, students are invited to tackle the problem individually. This time, however, the problem is a single task – one that will continue to be used in the main lesson. This time, the task is used to expose students’ different approaches to the problem. The common issues table for this task addresses such issues as: Does the student make sensible assumptions? Does the student use a sampling method? Is the sample chosen representative? As before, students’ responses are collected in by the teacher and analyzed, with the help of the common issues table (Figure 7).
2. The formative assessment lesson
The lesson begins with the teacher returning students’ initial individual attempts along with questions that are intended to move their thinking forward. Working individually, students review their attempts and try to respond to the teacher’s questions.
After this, the teacher asks students to get into small groups of two or three, and gives them an enlarged copy of the task (to facilitate sharing), poster paper and felt-tipped pens. Groups are invited to discuss the work of each individual, then come together to produce a poster showing a joint solution that is better than all of the group’s initial attempts. This activity promotes peer assessment and refinement of ideas. The teacher’s role is to observe the groups, challenging students to justify their decisions as they progress and thus refine and improve their strategies.
At this point, we suggest that the teacher chooses one or two contrasting solutions and asks ‘group representatives’ to present them to the class. This results in very different estimates being presented.
| Common issues: | Suggested questions and prompts: |
|---|---|
Student chooses a method which does not involve any samplingFor example: The student counts the trees. Or: The student multiplies the number of columns by the number of rows, and then halves this answer. |
|
Student chooses a sampling method that is unrepresentativeFor example: The student counts the trees in the first row/column and multiples by the number of rows/columns. Or: The student multiplies the number of trees in the left column by the number of trees in the bottom row. |
|
Student uses area and perimeter in their calculations |
|
Student makes incorrect assumptionsFor example: The student does not account for gaps. Or: The student does not realize that there are an unequal number of trees of each kind. |
|
Student calculates the number of trees in an unrepresentative sample area of the tree farm |
|
Students’ work is difficult to follow |
|
Student chooses an appropriate sampling method |
|
Student completes the task |
|
The teacher now introduces some “sample student work”, provided in the materials. This work has been carefully chosen to highlight different approaches and common mistakes. Each piece of work is annotated with questions to focus students’ attention. Figure 8 shows two examples of this work. The first (from Laura) contains some common mistakes that students make (ignoring gaps, assuming that there is an equal number of old and new trees), while the second (from Amber) introduces students to a sampling method they may not have considered. Introducing handwritten work from outside the classroom is helpful in that (i) students are able to critique it freely without fear of other students being hurt by criticism; (ii) handwritten ‘student’ work carries less status than printed or teacher-produced work and it is thus easier for students to challenge, extend and adapt it.
We have found that teachers like to be flexible in the way they distribute sample student work, in response to the particular needs of their own students. For example if students have struggled with a particular strategy, the teacher may want them to analyse a similar sample student work. Conversely if students successfully solved the problem using a particular strategy, then the teacher may want to them to analyse sample student work that uses a different strategy. The teacher can thus decide if their students would benefit from working with all the sample student work or just one or two pieces.
|
Laura attempts to estimate the number of old and new trees by multiplying the number along each side of the whole diagram and then halving. She does not account for gaps nor does she realize that there are an unequal number of trees of each kind. Can you explain why Laura halves her answer? What assumption is she making? |
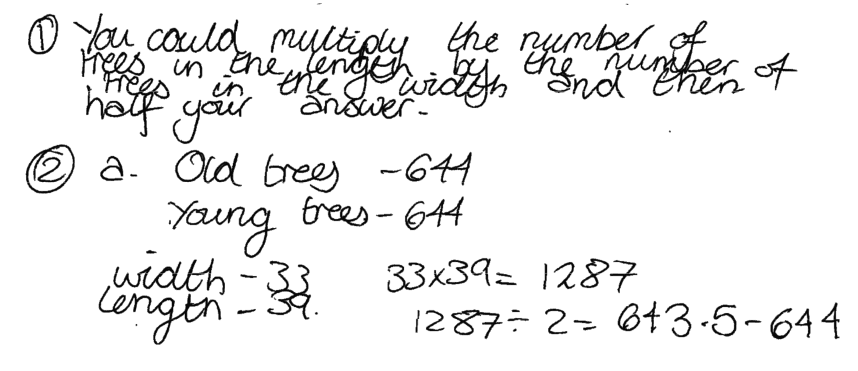 |
| Amber chooses a representative sample and carries through her work to get a reasonable answer. She correctly uses proportional reasoning. She checks her work as she goes along by counting the gaps in the trees. Her work is clear and easy to follow, although a bit inefficient. Can you explain why Amber multiplies by 25 in her method? |
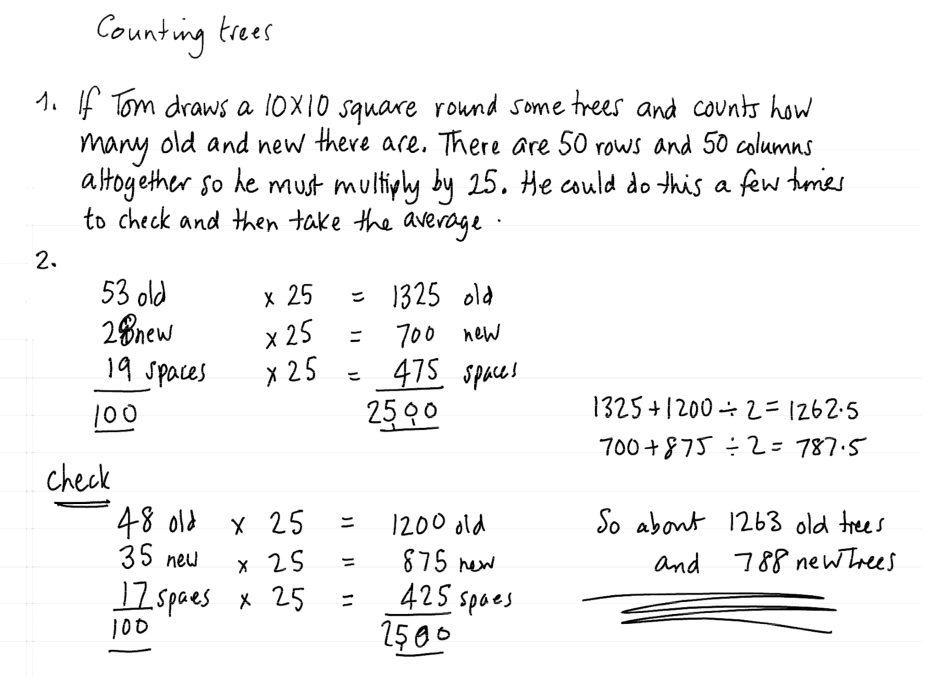 |
Feedback from early trials suggested that students struggled with their discussions of sample student work; they needed guidance beyond simply “imagine you are the teacher, assess this work”. In a later version, we added three or four feedback questions, specific to each piece of work. These questions did not just focus on the strengths and weaknesses of the approaches but also asked the student to provide corrective advice. So, for example: Does Laura’s approach make mathematical sense? Why does she halve her answer? What assumptions has Laura made? How can Laura improve her work? To help you understand Laura’s work, what question(s) would you ask her?
After critiquing the work, students may wish to refine their own approaches further. This process of successive refinement in which methods are tried, critiqued and adapted has been found to be extremely profitable for developing problem solving strategies. We often found that students changed their approach after seeing sample student work.
The lesson concludes with a whole class discussion that is intended to draw out some comparisons of the approaches used and, for this problem, the power of sampling. Students are invited to respond individually to such questions as:
- How was your group’s solution better than your individual solution?
- How did you check your method?
- How was your response similar to or different from the sample student responses?
- What assumptions did you make?
It was found that in most problem solving lessons, the evidence of learning was clearly visible in the successive refinements made to student work throughout the lesson, so this individual response takes the place of a post-lesson assessment task.
The teacher’s guide
The design of teaching materials involves two complementary challenges: devising a sequence of learning activities and teacher interventions that address the learning goals, then communicating with the teacher-user in a way that will enable them effectively to realize that activity sequence in their own classroom. The teacher’s guide for each lesson is the main route for this. In the descriptions above we have focused on the sequence of activities, noting in passing the guidance we give to teachers. Here we outline how that guidance is organized in the teacher’s guide for a typical problem solving lesson[11]. (A similar introduction to each lesson is given on the website version.)
One of the design constraints we faced was that, at any particular grade level, the lessons may be taught in any order. We therefore had to assume that each lesson might be a teacher’s first encounter with a Classroom Challenge. This resulted in each lesson containing rather more guidance than we would have wished to include.
Overview
The overview page lists the mathematical goals for the lesson together with explicit links to CCSSM. In the problem solving lessons the practices take precedence, and the content standards will typically be taken from several different content standards.
Students are able to choose which content areas to use in their initial tackling of the problem, so in this case, for example, they may not use the concept of random sampling. However, the sample student work in a lesson will confront students with this approach (as in Figure 8), so we do know that students will meet this content at some point in the lesson.
The introduction also gives the overall structure of the lesson, the materials needed and the time required. There are also references to PowerPoint slides that contain resources for whole class discussion, and occasionally applets or links to video clips that may be used.
Suggested presentation
After a description of the pre assessment task and the common issues table (Figure 7) we offer teachers detailed guidance on how to conduct the lesson. This is structured as we described above.
We include detailed directions on both the students’ activity and the teacher’s roles during this activity. This was done in response to requests from the teachers as to the nature of their new classroom roles. For example, at one point we say:
While students work in small groups, you have two tasks: to note their different approaches and to support student reasoning.
…and then go on to detail how they may do both of these, including suggestions for questions they may ask.
The design of teacher guidance presents a typical design trade-off. On the one hand, many mathematics teachers are accustomed to detailed guidance, even on familiar ground. When they are on new territory, as in these lessons, they expect (and most need) at least as much help with the new challenges that arise. On the other hand, if we provide too many pages of guidance it becomes indigestible – and perhaps unread.
The seven pages of guidance in “Counting Trees” represents a balance, heavily influenced by feedback from the trials, where the teachers consistently asked for more guidance. This is considerably more guidance than we initially intended to write! It implies substantial preparation the first time a Classroom Challenge is taught; something that both teachers and observers thought necessary in any case.
The complete teacher's guide can be downloaded from the online version of this article.
Formative assessment in the lessons
In summary, we see that in both concept-development and problem-solving lessons formative assessment opportunities arise in many forms.
- Teachers are given information on what students can do unaided.
- Teachers use this to offer differentiated support to students, as this is needed.
- Students gain constructive feedback, via other students and the teacher, as student work is discussed.
- Students act on feedback by refining and improving their responses.
- Teachers get feedback on learning by comparing the growth of student performance through the lesson and, in the case of the concept development lessons, by comparing pre and post assessments.
Outcomes and lessons learned
7This article has so far focused on the particular design challenges we faced in the Mathematics Assessment Project (MAP) and the design principles, strategies and tactics we used in developing the Classroom Challenges. This project is the latest stage in a fairly coherent program of “engineering research in education” (Burkhardt 2006) that goes back at least 35 years – indeed, in some respects to the foundation of the Shell Centre for Mathematical Education in 1967 as part of the first wave of “post-Sputnik” reform. MAP has taken this work in new directions, many of them with a strategic focus, reflecting the central role of the Classroom Challenges in the Bill & Melinda Gates Foundation’s program of reform.
We believe that this work has met its primary goals – that the evidence from the hundreds of lesson observations in the trials suggests that it is possible, through teaching materials alone, to enable typical teachers to realize high-quality formative assessment lessons in their classrooms. Further evaluative feedback, still ongoing, confirms this. Many questions remain; we look at some of them in this section.
On lesson design
The principles and tactics for lesson design used in this project and outlined above have been developed over several decades through two strands of work. The diagnostic teaching research program, developed and refined since its beginning in the 1980s, has provided the basis for the concept development lessons. Equally important has been a sequence of curriculum projects, often with examination boards, that have focused on substantial tasks as the focus of learning and teaching, as well as assessment. The lessons about design that we have learned from Testing Strategic Skills (Shell Centre 1984, Swan 1985), Numeracy through Problem Solving (Shell Centre 1987-89), the World Class Arena (Swan et al. 2002), and Bowland Maths (Burkhardt et al. 2008; Swan & Pead 2008a, 2008b) have underpinned the development of the problem-solving Classroom Challenges.
Two areas that we see in need of further design research are:
- Harnessing the potential of technology for formative assessment. We are currently beginning to explore how the power of technology may be used to make formative assessment even more powerful. Technology can be used to carry out pre-assessments of students and suggest possible follow-up actions based on this assessment. Classroom activities may be delivered in ways that provide immediate feedback to individual students and in ways that connect students socially so that they can offer peer support both within and outside the classroom. Such developments are not straightforward, however. Much current software focuses on improving procedural fluency that, ironically, technology has made obsolete. Assessment of conceptual understanding and problem solving strategies is rare by comparison. Existing assessment tools mostly use short or multiple-choice questions to deliver quantitative, summative feedback to the teacher rather than qualitative, formative guidance to the student. Our own experience in computer-supported teaching and learning over the past thirty years, suggests that technology has the power to do much better than this. It can provide rich and stimulating classroom experiences for collaborative work (for example, using ‘microworlds’ for investigation (Burkhardt et al. 2008;Swan & Pead 2008a, 2008b), and tools now exist for teachers to interact in new ways with students (see, for example, http://www.showbie.com/; https://classflow.com/).
- Developing a coherent curriculum. Our Classroom Challenges are not designed with any particular curriculum in mind. The issue of how these lessons may be integrated into coherent lesson sequences remains a significant design challenge. One idea that we are currently pursuing is that of curriculum curation, where we assist teachers in assembling coherent curricula from existing online classroom resources, embedding formative assessment into the process. Neither the concept nor the opportunity is new; a few school mathematics departments, dissatisfied with the limited range of mathematical practices that textbooks offer, have curated their curriculum for a long time. The idea is now, however, attracting more attention in response to the wealth of free, online resources that are becoming available. But the challenge of curating a scheme of work that is both rich and coherent is considerable. We aim to explore how to design and develop a practical process that links research and design expertise with the needs and ambitions of classroom teachers who want to bring into their school’s curriculum the richness that materials like the Classroom Challenges offer.
Beyond the classroom
Because of the relative low cost of teaching materials when compared, for example, with live professional development, this work has strategic implications, offering an economical way of releasing the power of formative assessment nationwide[12]. The impact on students and teachers in classrooms is already substantial, with around 3 million lessons downloaded across the United States at the time of writing. However, design issues remain if the challenges of implementing improvement are to be met equally well.
- Professional development. The design of PD has not received as much attention as the design of teaching and learning in classrooms. The MAP professional development modules, mentioned above, are part of a strand of our design research that shows real promise. But when one moves outside the classroom, getting rich and detailed feedback through observation becomes more difficult. We have had relatively little detailed feedback on teachers’ use of the modules, though a start has been made (Swan et al. 2013). There is much to be done in developing and establishing new standards for the design and development of PD resources, which still largely uses the “authorship” approach.
- Planned systemic change in which the outcomes are close to the intentions is, at least for changes as profound as these, an unsolved design problem. Unlike other fields which are recognized as research-based, medicine for example, politicians still feel free to base educational policy on their “common sense”. Changing this will depend on establishing a body of generally accepted research results – a challenge for the wider educational research community (Burkhardt and Schoenfeld 2003, Burkhardt 2013), which needs to give greater credit for systematic investigation of promising design principles across a range of variables of the kind that underpinned the work reported here. Systematic design research of this kind presents more difficult challenges than, for example, research at student or classroom level (Burkhardt 2006) but there have been examples of success (Black 2008, Burkhardt 2009). Perhaps the greatest current challenge is to get policy makers to recognize that this is an area where imaginative design and careful systematic development can help them in achieving the very similar goals for improvement in educational outcomes (Burkhardt 2014) that they all profess to seek. We are working on this.
- Informing the next phase of design and development is itself a formative assessment challenge. What is the pattern of use of the Classroom Challenges: in different kinds of classroom; with experienced or with novice teachers; with different levels of institutional or professional development support? Do teachers generalise the pedagogical and mathematical strategies and skills into broader adaptive expertise? In particular, how soon and how far do they carry over the practices of formative assessment into other lessons where it is not explicitly built in? Do they encourage self- and peer-assessment by students? Do they focus on reasoning, rather than answers and scores? This is the kind of information that any curriculum development project needs as a springboard for the next phase of design[13]. The MAP team is now exploring some of these questions, so far on a small scale.
We would like to thank many people for their support in this enterprise, notably the MAP team in the UK and the US[1], Carina Wong, Jamie McKee and the Bill and Melinda Gates Foundation for their foresight, support and guidance, and, particularly, the many teachers in whose classrooms these ideas and products have been developed and refined.
Footnotes
8[1] Better described as “periodic assessment”.
[2] The project as a whole, based at UC Berkeley, was directed by Alan Schoenfeld, Hugh Burkhardt, Daniel Pead, Phil Daro and Malcolm Swan. Malcolm Swan led the lesson design team, which included at various stages Nichola Clarke, Rita Crust, Clare Dawson, Sheila Evans, Colin Foster and Marie Joubert. The work was supported by the Bill & Melinda Gates Foundation; following initial planning with Carina Wong, our program officer was Jamie McKee. The US observers who provided the feedback from US classrooms were led by David Foster, Mary Bouck and Diane Schaefer, working with Sally Keyes, Linda Fisher, Joe Liberato and Judy Keeley..
[3] These were developed at the suggestion of President Barack Obama under the auspices of the US National Governors Association and the Council of Chief State School Officers. The United States Constitution makes it clear that education is a state, not a federal, responsibility - though federal governments have influence through offers of money for specific purposes.
[4] At the time of writing, around 3 million lessons have been downloaded.
[5] How far this will prove true remains unclear. That design challenge, too, is formidable, technically and politically.
[6] These materials can be found on the Mathematics Assessment Project (MAP) website: http://map.mathshell.org.uk/materials/index.php. They can be downloaded, free for non-commercial use. (The website gives details)
[7] … and, so often, boring.
[8] The need teachers have to have student scores for record keeping can be met in other ways, ideally by using periodic assessment with well-aligned tasks of the kinds, referred to above, that we have developed.
[9] Anne Brown, in her work on design research, coined the term “lethal mutations”.
[10] More detailed research on this design tactic is discussed in another paper in this issue (Evans and Swan, 2014).
[11] Direct links for the two teacher’s guides for the illustrated lessons may be found below:
The percents lesson: http://map.mathshell.org/materials/lessons.php?taskid=210
The counting trees lesson: http://map.mathshell.org/materials/lessons.php?taskid=422
[12] This was the Gates Foundation’s explicit aim in their approach to the Shell Centre team.
[13] It is expensive to collect and thus rarely funded. A back of the envelope estimate for understanding the outcomes of some of the NSF-funded curriculum projects suggested a cost comparable to that of the original development, approximately $100 million (Burkhardt 2009).
References
9Alexander, R. (2006). Towards Dialogic Teaching: Rethinking Classroom Talk (3 ed.). Thirsk: Dialogos.
Alexander, R. (2008). How can we be sure that the classroom encourages talk for learning? Here is what research shows. Cambridge: Dialogos.
Bassford, D. (1988). Fractions: A comparison of Teaching Methods. Unpublished M.Phil, University of Nottingham.
Beeby T, Burkhardt H, Fraser R E (1980) SCAN: a systematic classroom analysis notation for mathematics classrooms. Nottingham: Shell Centre 1980. http://mathshell.com/papers.php#scan
Bell, A. (1993). Some experiments in diagnostic teaching. Educational Studies in Mathematics, 24(1).
Black, P. (2008). In Response To: Alan Schoenfeld, Educational Designer, 1(3). Retrieved from http://www.educationaldesigner.org/ed/volume1/issue3/article12/index.htm
Black, P., Harrison, C., Lee, C., Marshall, B., & Wiliam, D. (2003). Assessment for learning: Putting it into practice. Buckingham: Open University Press.
Black, P., & Wiliam, D. (1998). Inside the black box : raising standards through classroom assessment. London: King's College London School of Education 1998.
Black, P., & Wiliam, D. (2009). Developing the theory of formative assessment, Educ Asse Eval Acc 21:5–31
Black, P., & Wiliam, D. (2014). Assessment and the design of educational materials, Educational Designer, 2(7), this issue. Retrieved from: http://www.educationaldesigner.org/ed/volume2/issue7/article24
Black, P., Wiliam, D., & Group, A. R. (1999). Assessment for learning : beyond the black box. Cambridge: University of Cambridge Institute of Education.
Brekke, G. (1987). Graphical Interpretation: a study of pupils' understanding and some teaching comparisons. University of Nottingham.
Brousseau, G. (1997). Theory of Didactical Situations in Mathematics (N. Balacheff, M. Cooper, R. Sutherland & V. Warfield, Trans. Vol. 19). Dordrecht: Kluwer.
Burkhardt, H. (2006). From design research to large-scale impact: Engineering research in education. in J. Van den Akker, K. Gravemeijer, S. McKenney, & N. Nieveen (Eds.), Educational design research. London: Routledge.
Burkhardt, H. (2009). On Strategic Design. Educational Designer, 1(3). Retrieved from http://www.educationaldesigner.org/ed/volume1/issue3/article9
Burkhardt, H. (2013). Methodological issues in research and development. In Y. Li & J. N. Moschkovich (Eds.), Proficiency and beliefs in learning and teaching mathematics - Learning from Alan Schoenfeld and Günter Törner. Rotterdam: Sense Publishers.
Burkhardt. (2014). Curriculum design and systemic change, in Y. Li & G. Lappan (Eds.), Mathematics Curriculum in School Education: Springer.
Burkhardt, H., Fraser, R., Coupland, J., Phillips, R., Pimm, D., & Ridgway, J. (1988). Learning activities & classroom roles with and without the microcomputer. Journal of Mathematical Behavior, 6, 305–338.
Burkhardt, H., & Schoenfeld, A. H. (2003). Improving Educational Research: towards a more useful, more influential and better funded enterprise. Educational Researcher 32, 3-14.
Burkhardt, H., Swan, M., & Pead, D. (2008). How risky is life?: Bowland Maths Case study. [online]. http://www.bowlandmaths.org/projects/how_risky_is_life.html. Bowland Trust/ Department for Children, Schools and Families.
DfES (2005). Improving Learning in Mathematics. London: Standards Unit, Teaching and Learning Division.
Dickson, L., Brown, M., & Gibson, O. (1984). Children Learning Mathematics. Eastbourne: Holt, Rinehart & Winston.
Evans, S. & Swan, M., (2014). Developing students’ strategies for problem solving: the role of pre-designed “Sample Student Work”. Educational Designer, 2(7), this issue. Retrieved from: http://www.educationaldesigner.org/ed/volume2/issue7/article26
Hart, K. (1980). Secondary School Children’s Understanding of Mathematics. A report of the Mathematics Component of the CSMS Programme. University of London.
Hart, K., Brown, M., Kerslake, D., Kuchemann, D., & Ruddock, G. (1985). Chelsea Diagnostic Tests. Windsor: NFER-Nelson.
Hatano, G., & Inagaki, K. (1986). Two courses of expertise. In H. W. Stevenson, H. Azuma & K. Hakuta (Eds.), Child development and education in Japan (pp. 262–272). New York: W H Freeman/Times Books/ Henry Holt & Co.
NGA, & CCSSO (2010). Common Core State Standards for Mathematics. Retrieved from http://www.corestandards.org/Math
Onslow, B. (1986). Overcoming conceptual obstacles concerning rates: Design and Implementation of a diagnostic Teaching Unit. Unpublished PhD, University of Nottingham.
Shell Centre (1984). Swan, M., Pitts, J., Fraser, R., and Burkhardt, H, with the Shell Centre team, Problems with Patterns and Numbers, Manchester, U.K.: Joint Matriculation Board and Shell Centre for Mathematical Education, retrieved from http://www.nationalstemcentre.org.uk/elibrary/resource/349/problems-with-patterns-and-numbers
Shell Centre (1987-89) Swan, M., Binns, B., & Gillespie, J., and Burkhardt, H, with the Shell Centre team. Numeracy Through Problem Solving: five modules for teaching and assessment: Design a Board Game, Produce a Quiz Show, Plan a Trip, Be a Paper Engineer. Be a Shrewd Chooser, Harlow, UK: Longman, retrieved from http://www.nationalstemcentre.org.uk/elibrary/collection/159/numeracy-through-problem-solving
Swan, M. (1983). Teaching Decimal Place Value - a comparative study of ‘conflict’ and ‘positive only’ approaches. Paper presented at the 7th Conference of International Group for the Psychology of Mathematics Education, Jerusalem, Israel.
Swan, M. (1985) Swan, M. with Pitts, J., Fraser, R., and Burkhardt, H, and the Shell Centre team (1985) , The Language of Functions and Graphs, Manchester, U.K.: Joint Matriculation Board and Shell Centre for Mathematical Education , retrieved from http://www.nationalstemcentre.org.uk/elibrary/resource/350/language-of-functions-and-graphs
Swan, M. (2000). GCSE mathematics in Further Education: Challenging beliefs and practices. The Curriculum Journal, 11(2), 199-233.
Swan, M. (2006a). Collaborative Learning in Mathematics: A Challenge to our Beliefs and Practices. London: National Institute for Advanced and Continuing Education (NIACE) for the National Research and Development Centre for Adult Literacy and Numeracy (NRDC).
Swan, M. (2006b). Designing and using research instruments to describe the beliefs and practices of mathematics teachers. Research in Education, 75, 58-70.
Swan, M. B. (2006c). Learning GCSE mathematics through discussion: what are the effects on students? Journal of Further and Higher Education, 30(3), 229-241.
Swan, M. (2008). A Designer Speaks: Designing a Multiple Representation Learning Experience in Secondary Algebra. Educational Designer: Journal of the International Society for Design and Development in Education, 1(1). Retrieved from: http://educationaldesigner.org/ed/volume1/issue1/article3/index.htm
Swan, M. (2014). Improving the alignment between values, principles and classroom realities. In Y. Li & G. Lappan (Eds.), Mathematics Curriculum in School Education: Springer.
Swan, M., Burkhardt, H., Crust, R., Bell, A., & Pead, D. (2002). World Class Tests in Problem Solving. QCA. See: http://www.worldclassarena.org
Swan, M., & Green, M. (2002). Learning Mathematics through Discussion and Reflection. London: Learning and Skills Development Agency.
Swan, M., & Pead, D. (2008a). Bowland Maths Professional development resources. [online]. http://www.bowlandmaths.org.uk/pd: Bowland Trust/ Department for Children, Schools and Families.
Swan, M., & Pead, D. (2008b). Reducing road accidents: Bowland Maths Case study. [online]. http://www.bowlandmaths.org/projects/reducing_road_accidents.html. Bowland Trust/ Department for Children, Schools and Families.
Swan, M., Pead, D., Doorman, M., & Moolddijk (2013). Designing and using professional development resources for inquiry-based learning. ZDM - The International Journal on Mathematics Education, 7.
Wiliam, D., & Thompson, M. (2007). Integrating assessment with instruction: What will it take to make it work? In C. A. Dwyer (Ed.) The future of assessment: shaping teaching and learning (pp. 53-82). Mahwah, NJ: Lawrence Erlbaum Associates.
About the Authors
10Malcolm Swan is Director of the Centre for Research in Mathematical Education at the University of Nottingham, which incorporates the Shell Centre for Mathematical Education team. He has led the design teams in a sequence of Shell Centre research and development projects. He led the diagnostic teaching research program that established many of the design principles set out in this paper. In 2008 he was awarded the first ISDDE Prize for educational design, for The Language of Functions and Graphs.
Hugh Burkhardt is a former director of the Shell Centre for Mathematical Education at the University of Nottingham, and has directed a wide range of projects in both the US and the UK, often working with test providers to improve the validity of their assessments. The strategy is to link assessment, curriculum and professional development to embody high standards for learning and teaching. In 2013 he was awarded the ISDDE Prize for educational design, for lifetime achievement.