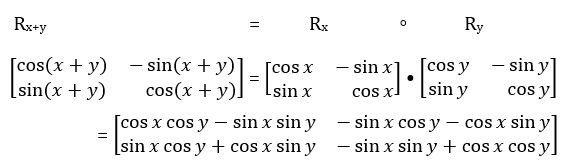Beauty and Serendipity in Teaching Mathematics
Zalman Usiskin
Abstract
i
Serendipity has been defined as the occurrence and development of events by chance in a happy and beneficial
way. Beauty is described by one dictionary as “a combination of qualities, such as shape, color, or form,
that brings pleasure to the senses or pleasurably exalts the mind or spirit.” This paper gives examples of how these
two aspects of experience have influenced what I would like to see in mathematics classrooms and my curriculum
development work to engender them, prior to and through the work of the University of Chicago School Mathematics
Project.
Introduction
ii
The opportunity to write this paper arose from my receiving one of two 2017 ISDDE prizes for lifetime achievement in
curriculum design and development, the other going to Kaye Stacey. This paper is based on a plenary talk presented
at the 2018 ISDDE conference in Galway, Ireland.
I would not have received this award without the work of many other people. It is common to say that we work on the
shoulders of giants but actually, we work at the feet of such people as Polya or Freudenthal or Klein, and the
numerous great mathematicians and educators over the ages and over the world who have created the field that is our
playground. But we do work shoulder to shoulder with our coworkers and our colleagues, and our students, from whom
we learn much, and we are helped by their labors.
It is particularly special to receive this award because it comes from my peers. I wish to thank the members of the
award committee, and especially thank Bob and Barbara Reys for their work in putting together the documents for my
nomination and to those who wrote supporting letters. Those people contributed directly to my receiving this award.
But there are dozens of other people – no, hundreds of other people – without whom I would not be standing before
you. Some will be identified here but I cannot possibly name all of them.
I also would not be here were it not for serendipity, many fortunate circumstances that came to me without any work
on my part. So I decided to make serendipity one of the themes of these remarks.
Fortunate geography
iii
I was born in Chicago and, after graduating high school, went to the flagship university in my state, the University of Illinois, because my brother went there. I had decided years earlier that I wanted to teach mathematics.
My first education course was titled “Introduction to Education” and I was in the section for prospective mathematics teachers. The teacher in this class was Kenneth Henderson, a professor of mathematics education and a gifted teacher. Some years later his doctoral students included John Dossey and Tom Cooney. The subject matter for this class included detailed study of the secondary school materials developed by the University of Illinois Committee on School Mathematics (UICSM). UICSM, which had been started in 1951 by Max Beberman (Beberman, 1958), was the first of the “new math” projects in the United States (Kinsella, 1965).
UICSM’s materials (UICSM, 1959; Beberman and Vaughan, 1964) began with a lesson that in its time was famous, a correspondence by handwritten letter between a student in the contiguous United States and a student in Alaska, in which the first student wants to help the Alaska student and, to determine the needs of the Alaska student, asks the Alaska student several questions.
Among these are: “Take 2 away from 21.” The Alaska student writes “1”. “How many times does 3 go into 8?” The Alaska
student answers “twice”. “Write a number bigger than 4.” The Alaska student writes 4.
The purpose of the lesson was to show that what you write is a representation of the concept of number, not the number itself. And what you write is a numeral, and this lesson taught the distinction between number and numeral. None of us university students had ever thought about this distinction.
UICSM was very careful in its use of language but went overboard on this particular idea. A letter such as
x, as used in an equation, was not called a variable, but a pronumeral, because it stood for a
numeral in the same way that a pronoun stands for a noun. Descriptions of algebraic properties such as the
distributive property of multiplication over addition were preceded by quantifiers: ∀a,∀b,∀c,a(b + c) = ab + ac. The existence of an identity was
described by: ∃b∋∀a,a + b = a. By carefully basing the solving of equations and the manipulation of algebraic expressions on these
properties, UICSM brought mathematical systems and proof into the study of algebra, ideas that had not previously
been part of the study of that subject.
I loved the approach. But more than that, I loved the fact that the mathematics that I had been taught in one manner could be approached in a significantly different manner. UICSM taught us that it was not only OK, but more – that it was valuable – to carefully look what was being taught, because a careful examination of the mathematics might result in a better treatment.
There are only a few other universities in the country where I could have received a comparable lesson. And why did I get this education? Because Illinois was my state university and my brother went there. This is serendipity, the occurrence and development of events by chance in a happy or beneficial way.
UICSM organized algebra in a coherent way. It was beautiful. No more learning of isolated rules. Everything could be traced back to the field properties of real numbers.
Five years later, when I became a full-time teacher, I taught out of materials very much influenced by SMSG, the largest of the new math projects in the U.S. Like the Illinois materials, SMSG traced the properties used in algebra back to the field properties of real numbers. Not as severe an approach as UICSM, but again a manifestation of the possibility of approaching a standard mathematics course in a significantly different way than had previously existed, a way that was mathematically more coherent than I had ever seen. It met the criterion of being beautiful, for it pleased my senses and exalted my mind and spirit. The beauty of mathematics makes it possible to have beautiful lessons, units, and courses in mathematics.
Taking Advantage of Serendipity
iv
Some years ago, I was observing one of my master’s degree students teaching a 12th-grade class as part of her student
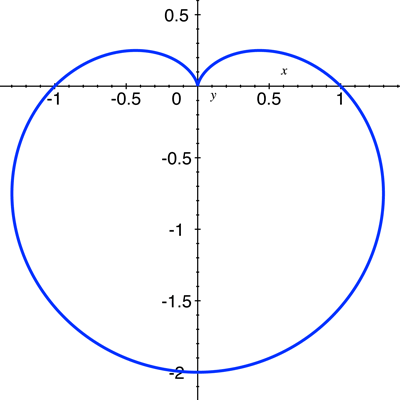
teaching experience. The topic of the day was graphing in polar coordinates and one of the examples was that of a
cardioid (see Figure 1 ).
The cardioid receives its name because it is heart-shaped. Sitting in the back of the room, I realized that the date
that day just happened to be February 14th, Valentine’s Day in the U.S.A. (and in many other countries throughout
the world). And so I waited for this student teacher to point out that this curve roughly resembles the heart on a
Valentine’s Day card.
The connection never was mentioned. Here was a traditional precalculus class in which connections between mathematics and the real world were almost entirely absent, and here was a chance to show at least a little bit of a connection, and the opportunity was lost. It was a coincidence that this topic fell on Valentine’s Day. It was an opportunity for serendipity, a chance encounter that I think would have delighted students.
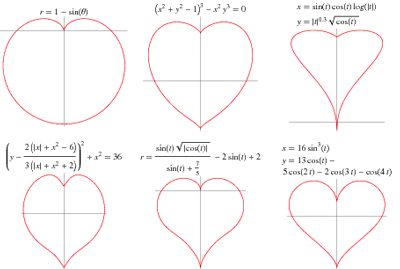
Of course, the Valentine heart does not look exactly like a cardioid, so people have experimented with various
mathematical expressions to show graphs that are more like Valentine hearts or the hearts found on playing cards.
Figure 2 displays some of the variety of expressions that give rise to curves somewhat like the Valentine
heart. I particularly like the middle curve in the top row, the graph of a 6th degree equation in x and
y with a rather short algebraic description. With appropriate scaling it is almost congruent to a Valentine
heart. It provides an aesthetically beautiful example of the power of algebra to mathematically model real objects.
A well-designed curriculum will make it clear for students to see that mathematics can model even complicated
geometric figures. And it will show or lead the student to other beautiful curves with nice mathematical
descriptions.
Source: Weisstein, Eric W. "Heart Curve." From MathWorld – A Wolfram Web Resource. http://mathworld.wolfram.com/HeartCurve.html
How could this student teacher ever miss the connection between the cardioid and Valentine’s day? One reason is that
the most common placement of the cardioid is with a horizontal symmetry line. Another reason is that the cardioid is
in the curriculum because it provides a nice example of a curve described in polar coordinates r and
θ rather than x and y, not because of its connection with hearts or valentines. Routine
and tradition often get in the way of serendipity and often inure us to the beauty in what we teach.
The Elegance of Transformations
v
Beauty in mathematics takes many forms. One of the forms is elegance. As a doctoral student at the
University of Michigan, I was looking for topics on which I might write a dissertation, and Joseph (Joe) Payne, my
advisor, suggested that I might investigate using transformations such as reflections, rotations, translations and
so on, in geometry. I looked into the idea and liked it. I was enthralled by the elegance of the definition of
congruent figures in this approach. In a traditional approach, a different definition of congruence is needed for
each different type of figure. Using transformations, only one definition is needed. Table 1 shows this.
Joe said it was not he who was interested in this idea, but Art Coxford, a younger professor at the university. Art thought that it might be the usual curriculum dissertation – write a 3-week or 6-week unit, try it out, and do some comparison with traditional classes to see if there were any differences, but by this time Ken Henderson and I had already written the manuscript for a full-year precalculus text (Henderson, Usiskin & Zaring, 1971). I argued that 3-week and 6-week units never influenced what was taught more generally, so we should write a full-year course utilizing transformations. And so we decided that during the following school year we would write together and each of us would pilot a full-year 10th-grade geometry class using what we had written.
In the summer, serendipity rose again. I was working as assistant director of a U.S.A. National Science Foundation (NSF) summer institute for teachers. In the office library of the director, Phil Jones, I found a book using transformations, Transformatiemeetkunde, written by a Dutch team led by Rudolf Troelstra (Troelstra, Haberman, deGroot & Bulens 1965). In this book, the first thing done with a figure was to prove its symmetry, from which so many other properties can be derived automatically.
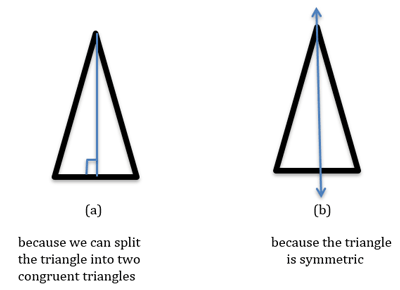
For instance, one of the first theorems studied in high school geometry is that the base angles of an isosceles
triangle are congruent, i.e., they have the same measure. In the traditional approach, we split the isosceles
triangle into two triangles by drawing a segment from the vertex angle to the midpoint of the base
(Figure 3a).
The two triangles thus formed are congruent by SSS (side-side-side) and the base angles, being corresponding
angles of these triangles, must thus be congruent. In the transformation approach, we deduce that the triangle is
its own image under a reflection over that bisector, and since one base angle is the image of the other, they must
be congruent (Figure 3b).
The transformation approach takes advantage of our intuition about reflection-symmetric figures and can be applied to
obtain some basic properties of parallelograms, rectangles, squares, regular polygons, conic sections, and many
other figures (Coxford & Usiskin, 1971, 1972). In this way,
transformations present an elegant and intuitive way of approaching Euclidean geometry, appropriate not only for
students who will be studying more mathematics but also for students who have difficulty visualizing and organizing
properties of figures. My doctoral dissertation, undertaken using a revision of the pilot materials, compared the
performance and attitudes of 425 students using these materials with 475 students using traditional geometry
materials (Usiskin, 1972). The commercial edition incorporated a further
revision based on the results of the dissertation study.
The development of the course Geometry – A Transformation Approach occurred in the late 1960s, just before Escher drawings became known in the U.S.A. Just when the commercial edition appeared in 1971, Harold Jacobs had put an Escher drawing on the cover of his landmark book Mathematics – A Human Endeavor (1971). Quickly Escher’s work was seen everywhere, the word tessellation entered our vocabulary, and we saw congruent horses, birds, fish, and all sorts of other figures. Beautiful art and beautiful mathematics.
The Study of Patterns
vi
A number of people have described mathematics as the study of patterns, that is, the study of similarities
in structure. Perhaps the most well-known writing about mathematics and patterns is due to G.H. Hardy (1940).
“A mathematician, like a painter or a poet, is a maker of patterns… The mathematician’s patterns, like the painter’s or the poet’s must be beautiful, the ideas, like the colours or the words, must fit together in a harmonious way. Beauty is the first test; there is no permanent place in the world for ugly mathematics.”
There is something particularly satisfying in realizing that some mathematical properties that look different are instances of the same pattern. But in this regard, mathematics is not at all unique. Researchers in every field look for commonalities. What mathematics does is to describe the patterns algebraically or geometrically, and then study the patterns themselves often without regard for their origins.
The descriptions of patterns are so etched in our mind that the letters we use are all that is needed to indicate the
setting. As an example, Table 2 shows six equations that are mathematically identical. In each, the product of
two numbers is a third number. They differ only in the letters used to identify the numbers, but that is enough to
let us know the kind of situation that they describe. The reader might wish to cover the right column of this table
and guess what each equation in the left column represents.
Another example of the significance of letters involves the graphing of parabolas, which is a topic in all U.S.
algebra texts, usually in the second year of algebra study. Students learn that the vertex of the parabola with
equation y = (x + 3)2 + 5 can be seen in its equation. Today they may even connect the algebra with geometry, namely that the graph
of y = (x + 3)2 + 5 is a translation image of the parabola with equation y = x2. What they do not learn from most U.S. textbooks is the
general theorem that applies to all translation images (Usiskin, 1975). In a relation described by a sentence in
x and y, the following two processes yield the same graph: (1) replacing x by
x–h and y by y-k; (2) applying the translation T(x,
y) = (x+h, y+k) to the graph of the original relation. Some
consequences of this Graph Translation Theorem are shown in Table 3.
The immediate corollaries to the Graph Translation Theorem permeate many topics in high school mathematics. However,
they are disguised because the particular letters h and k that signal the magnitude of the
translation usually appear only with the circle and parabola. Symbols such as x0, y0, m,
and b are used, and most students do not realize that all the corollaries are special cases of the same
theorem. They are not told that the graphs of the sine and cosine functions are congruent, and that graphs of all
exponential and logarithm functions with the same base are congruent. In the U.S.A., we have had for many decades a
controversy concerning whether it is better to have a 3-year algebra-geometry-algebra sequence or what is called an
integrated sequence. Here is a wonderful example of an integration of algebra and geometry that should be in both
sequences but is to my knowledge only found in the UCSMP materials. But the groundwork was done much before UCSMP
existed.
The translations of coordinate graphs that are the subject of the Graph Translation Theorem are accomplished by
adding fixed values to the coordinates of the preimage. A beautiful corresponding multiplicative structure yields
stretches and shrinks of graphs. We call this theorem the Graph Scale Change Theorem (Usiskin, 1975;
Rubenstein, Schultz, Senk, Hackworth, McConnell & Viktora,1992). In a relation described by a sentence in x and
y, the following two processes yield the same graph (1) replacing x by x/a and
y by y/b; (2) applying the scale change T(x, y) = (ax,
by) to the graph of the original relation.
Where we added before, we multiply here. Where we subtracted before, we divide. Again, there are numerous useful
corollaries, the most common of which are shown in Table 4 . Among the corollaries are that all parabolas are
similar, that all rectangular hyperbolas are similar, and that the graphs of all exponential and logarithm functions
are similar regardless of base. In creating curriculum for students, I have felt it important to include these
wonderful unifying theorems – beautiful elegant mathematics.
Approaching algebra through applications
vii
While I was playing out the curricular manifestations of the beautiful mathematics of matrices and groups associated
with transformations, my colleague at the University of Chicago, Max Bell, was writing about the fundamental
importance of applications in the learning of mathematics (Bell, 1972). Max
was a powerful champion of incorporating the real world into the mathematics classroom. He argued (as
Thorndike,
Cobb, Orleans, Symonds, Wald & Woodyard. (1923)
had argued decades before) that the traditional “word problems”
(or “story problems”) found in algebra texts – those dealing with coins or age or whole-number digits - were not
actual applications. I became convinced he was right.
At that time, about three-fourths of high school graduates in the U.S.A. completed one year of algebra and only half of these completed a second year, yet books for the two courses were written in the same style as if they were for the same population. I felt they needed different styles; the first course had to be appealing to everyone. And so, in 1973, I applied for and received an NSF grant to develop a beginning algebra course in which the algebra would be developed from applications and there would also be probability and statistics. I found a typical school and worked out a relationship as I had in other places, namely to teach an algebra class every day for the entire year and have someone else teach the same lesson later in the day to a class of similar students.
How does one begin such a course? Max had written about uses of numbers and uses of the four basic arithmetic operations, so I began there and expanded the discussion to uses of variables. This would naturally lead to real-world situations leading to expressions and linear equations of the type a + x = b, ax = b, ax + b = cx + d, and into the various manifestations of the distributive property, graphing of lines, and, by extending multiplication into integer powers, the discussion could lead to compound interest and exponential functions. Quadratic expressions and equations could be handled by standard applications to counting, area, and acceleration.
But I had no idea how I would use applications to get to polynomial expressions. And then, in this 9th-grade class,
as we were discussing compound interest, a student raised his hand with a question. He said, “I was going over my
homework with my father and he asked me whether this mathematics has anything to do with the amount we pay on our
mortgage.” I thought, “His father has solved my problem.” From this came a lesson to introduce polynomials that I
have never seen anyone copy. The lesson begins with the following problem (Usiskin, 1979), shown here in
Figure 4.
After the solution is given in the lesson, the answer is parsed (as shown in Figure 4 ) and the various components of the polynomial expression are changed to show the contribution of coefficients and exponents. At this stage of schooling, a general formula for computing what a mortgage will cost is not reasonable, for that takes some knowledge of the sum of a finite geometric series. But the germ of the idea is here.
I don’t know how I would have approached polynomials in this course if that student had not relayed a question from his father to me. I do know that this was one of many times when the content of my writing was significantly affected by something that happened in class as I was teaching. Teaching promotes the probability that something serendipitous will occur.
Serendipity and Statistics
viii
Forty years ago, statistics in school mathematics texts in the U.S.A. referred only to the calculation of the mean, median, and mode, usually done in grades 7 and 8, before high school. But when looking for real-world applications of mathematics involving algebra, I kept bumping in to statistics.
Serendipity placed Bill Kruskal in my faculty neighborhood. Bill was a professor of statistics at Chicago, a past chair of that department, and one of the first members of the joint committee of NCTM and the American Statistical Association on statistics in schools. I asked Bill if he would look at the statistics in the algebra materials I was creating, and he agreed.
Bill was a tough reader. He scribbled all over my manuscript. He asserted that statistics is not a subset of mathematics. It is applied mathematics, like operations research or physics, because problems in statistics originate in a setting outside of mathematics, and to do statistics, a person needs to know knowledge of the setting outside of mathematics as well as the appropriate mathematics.
Bill was proud to be a statistician at Chicago. At Chicago, the statistics department had separated from the mathematics department shortly after the second world war, and the statistics faculty was firm in the belief that statistics was a discipline in its own right. The first lines of the book The Nature of Statistics (Wallis & Roberts, 1954) assert that view.
“Statistics is a body of methods for making wise decisions in the face of uncertainty…This modern conception of the
subject is a far cry from that usually held by laymen. Indeed, even the pioneers in statistical research have
adopted it only within the past decade or so.”
(Wallis & Roberts, 1954)
For curriculum makers, this difference is noteworthy. Mathematics texts often employ the terms theoretical probability and experimental probability to distinguish between, for example, the (theoretical) probability of tossing a fair coin (½) and what you get when you toss the coin (something near ½). Bill Kruskal argued that all probabilities are theoretical and that what mathematicians call experimental probability is more accurately described as relative frequency.
Books often have problems with the following wording: If you toss a fair die, what is the probability of 3 heads in a row? Statisticians would say that you cannot toss a fair die. Whether a die is fair or not cannot be absolutely determined. You can only imagine tossing a fair die. You can suppose a die is fair and then reason from that. It is more than semantics. Looked at in this way, problems in probability provide wonderful examples of deduction from assumed statements.
Statistics has evolved in the past four decades. A more current definition is that “Statistics is the science of data.” (Yates, Moore & Starnes, 2003).
Applying Arithmetic
ix
The decade of the 1970s was a down time in mathematics education in the United States, quite a bit like our current decade. Except for my algebra project, NSF was no longer funding curriculum development in mathematics. A backlash to the ‘new math’ of the sixties was very much influenced by behaviorism, causing many schools to focus on behavioral or performance objectives that were mostly manipulative skills in arithmetic and algebra, not too different from today’s Common Core (National Governors Association Center for Best Practices, Council of Chief State School Officers, 2010). Programmed learning materials were breaking the curriculum into little steps, not too different from today’s adaptive formative and summative testing. And all this in the same decade as the introduction of hand-held calculators. What was there to teach if calculators could do all the arithmetic?
In 1976, Max Bell and I were asked to write an essay on that question by Marilyn Suydam, who with Dick Shumway at Ohio State University was writing a report for NSF on electronic calculators (Suydam, 1976). Our essay, 75 pages in length, was an appendix to that report. And we had only scratched the surface. So, we applied to NSF for a grant to write materials about applying arithmetic, for we felt that with calculators, the focus of the curriculum should be on the uses of arithmetic rather than on arithmetic algorithms. The result was a manuscript of over 500 pages (Usiskin & Bell, 1983) that we split into three parts, numbers, operations, and maneuvers (rewriting, estimating, transforming, displaying).
As we were writing this manuscript, it became apparent that the named properties of the operations of
arithmetic in books are all pure mathematics: multiplication is associative and commutative, has the identity 1, is
distributive over addition, etc. But the fundamental uses of the operations are not given that kind of
status. We called these use meanings and the principal ones are shown in Table 5.
(From Usiskin & Bell, 1983)
Our view was that because these use meanings were what made the operations important outside mathematics, they were the origins of the abstractions that created the mathematics, and that the use meanings should be properties taught to students with as much importance as the purely mathematical properties that are in the curriculum.
Others (e.g., see Carpenter, Moser & Romberg, 1982; or Stigler, Fuson, Ham & Kim, 1986) have detailed more kinds of word problems relating to arithmetic operations than we did, but our perspective was from the standpoint of basic meanings from which other meanings can be derived. The result is a very nice blending of pure and applied mathematics. For instance, it is obvious that put-together and take-away undo each other, but so do size change and ratio. That is, if two similar figurines are 15 and 25 cm tall, then ratio division tells us that the larger figurine is 5/3 the height of the smaller. The number 5/3 is the size change factor; if we multiply 15 by 5/3 we get 25. Similarly, both rate factor and acting across multiplications arise from rate division. If we do not bring these uses out into the open, we are teaching just like that student teacher with the cardioid; the uses are looking at us in the face, but we are ignoring them.
The van Hiele theory
x
At around this time, Izaak Wirszup, a professor of mathematics at the university, was touting a stage theory developed by Pierre van Hiele and Dina van Hiele-Geldof, students of Hans Freudenthal in the Netherlands. Wirszup reported that this theory had been used by the Soviet mathematician Pyshkalo in constructing a curriculum for young students. Researchers in the U.S.A. became enthralled with the theory, which suggested that a student needs to go through the following stages in understanding geometry, and in this order: recognition, analysis, order, deduction, and rigor.
The theory is elegant. A student cannot be at van Hiele level n without having gone through level n-1. What is intrinsic at level n-1 becomes extrinsic at level n. Each level has its own linguistic symbols and its own network of relationships. Two persons who reason at different levels cannot understand each other. This theory was employed to explain some difficulties students encountered in the then-typical high school geometry course in the U.S.A.
I was skeptical about this theory, particularly about the first property. I felt that I did not go through these stages, nor did many others of my generation. In those days, students dove into the study of geometry at level 3 or level 4. Sharon Senk, a doctoral student at the time, and I decided to apply for funding from the National Institute of Education to test the theory. We devised a crude test of questions at each level based on writings of Pierre and Dina van Hiele, and we ran those by him in person when he visited the University of Chicago. We gave the test to about 2400 geometry students in 5 states in the U.S.A. and found, as Wirszup had predicted, a majority of students were at levels 1 and 2 and could not be expected to succeed in a proof-oriented geometry course. We also found that there were students who could not be assigned a level. Levels were reasonably predictive of performance in the geometry course, but so was a simple content test given at the beginning of the year.
The test we devised (Usiskin, 1982) has been translated into at least 10 languages and used in dozens of master’s theses and PhD. Dissertations. Virtually everyone who uses the test assumes the theory is valid and does not consider that our test was designed to test the theory.
UCSMP and Serendipity
xi
My association with UCSMP came as a result of again being in just the right place at just the right time. In the fall of 1982, just as we were completing the van Hiele research and the Applying Arithmetic manuscript, Izaak Wirszup was working on the possibility that the university could receive a 6-year grant of $6 million dollars from the Amoco Foundation, the charitable arm of the Amoco Corporation (now BP), if we were interested and the university would allow a project with such an unprecedented length and funding. It was not obvious that the university would agree to such a project because something of this magnitude requires a great deal of office and work space, and space is a very valuable commodity in a university.
Izaak and Paul Sally from the Department of Mathematics, myself, Larry Hedges, and Susan Stodolsky from the Department of Education met weekly into the spring of 1983. We proposed a K-12 project in mathematics that would be informed by work done all over the world in order to create and test a full mathematics curriculum for the vast majority of U.S. students. We were supported by the chairs of our departments, Felix Browder and Charles Bidwell. The two department chairs, Izaak, Paul, and I – five full professors - brought our case to the provost of the university. The provost said the university could afford space for a $5 million project. We knew we needed a total of about $12 million to do what we envisioned (equivalent to about $30 million today), but we did not tell that to the provost. The provost approved the project under the condition that the Amoco Foundation not reduce its other giving to the university. The Foundation kept its word.
From the start, we split the project into four components: a resources component headed by Izaak that would translate materials from other countries to fuel the work of an elementary component in grades K-6 and a secondary component in grades 7-12, and an evaluation component headed by Larry and Susan for quantitative and qualitative research of the work done by the grade-level components.
It was felt that in order to change, the first work at K-6 would need to be in the realm of education of teachers. Paul Sally and a local teacher, Sheila Sconiers, headed this component. It was understood that I would direct the 7-12 component. Unlike those dealing with grades K-6, I felt that teachers in grades 7-12 needed to see materials before they would change. The existence of UCSMP provided a unique opportunity to bring together the various assorted pieces of work that had occupied my time for the preceding 16 years. What this meant is that the main themes and many of the detailed developments of the earlier work - applications, transformations, the use of calculator technology – could be carried over.
At the start of UCSMP, Max Bell was on leave from the university. It would be two years before he came back and then he began the design and development of a UCSMP curriculum for grades preK-6, a curriculum still quite successful commercially under the name Everyday Mathematics (UCSMP, 2016). Today that effort is headed by Andy Isaacs. Appendix A gives full details of the published, pre-publication and test versions of the secondary UCSMP materials. In doing this, the appendix also indicates the amount of work behind the commercial editions.
Two Competing Beautiful Aspects of Mathematics
xii
In the European tradition, we tend to think of Euclid’s Elements (Heath, 1956) as the first mathematics textbook. It certainly was the most influential in instilling proof as the determining factor regarding the truth of a mathematical statement. In this regard, the development of all the geometry and number theory in the Elements is a thing of beauty. For two millennia, it was the major influence on geometry teaching in Europe and later in the Americas.
Algebra developed separately from geometry. Even though Descartes and Fermat developed analytic geometry in the 1600s less than a half-century after Viete’s pioneering work with variables, Euler’s 1770 Vollständige Anleitung zur Algebra (Complete Instruction in Algebra), a prototype for the algebra texts that followed, contains no geometry (Euler, 1972).
At the end of the 19th century, well over 100 years ago, two U.S. national reports (National Education Association, 1894; Young, 1899) established a year course in algebra followed by a year course in demonstrative geometry as 9th and 10th grade courses for students at grade level in mathematics. “Demonstrative” meant that the geometry course was very much proof-oriented, with theorems demonstrated by proofs. In contrast, though rules or properties would be given as justification for steps in solving equations or simplifying expressions, the algebra course had no mention of proof. Slowly the geometry course became followed by a second full-year course in algebra, perhaps with some trigonometry, again with little or no proof. And thus, an algebra-geometry-algebra sequence became fixed in most school districts; furthermore, the algebra courses contained little if any geometry and the geometry course contained little if any algebra. Today that sequence starts in 8th grade for somewhere around one-third of students in the U.S.A.
The work with applications of algebra showed that one reason that students could not apply algebra was that they could not apply arithmetic beyond small whole numbers. The van Hiele work had showed that most students entered a high school geometry course with too little knowledge of geometry to perform well in the course. So, even before the start of UCSMP, I had decided to go into a school in the fall of 1983 to write and teach a book that would integrate applications of arithmetic with preparation of students for algebra and geometry. That book became Transition Mathematics.
While Transition Mathematics was being written, we brought in six of the best curriculum development people in the country as an advisory group to assist in determining what the next five courses would be. A major issue concerned the algebra-geometry-algebra sequence. From the early 20th century, there had been advocates to integrate the algebra and geometry, i.e. to teach some geometry and some algebra each year, and books implementing an integrated curriculum were known to us although they were only sparingly found in schools. So, one of the first questions facing us at UCSMP was whether we should integrate algebra and geometry in the years following Transition Mathematics.
Many of the advisory group were known to favor a 3-year sequence that would cover the traditional algebra and geometry content without having all the geometry in one year. The result of the group thinking was a first year that was almost all algebra with a little geometry, a second year that began with a lot of algebra and ended with a lot of geometry, and a third year that continued the geometry work and ended with a lot of algebra.
Ultimately it was my decision to keep the algebra-geometry-algebra sequence because the alternative created by this group was close to that sequence and I did not want to fight state, district, and school adoption requirements that typically required two algebra courses and one geometry course. I felt that we could involve geometry applications throughout our algebra courses and involve algebra throughout our geometry courses. The result was a first course that might be described as an “algebra train” on which the passengers are arithmetic, geometry, and statistics; a second course that might be described as a “geometry train” on which there are algebra passengers; and a second “algebra train” course in which geometry and trigonometry are passengers. All this takes advantage of a beautiful aspect of mathematics; that mathematics is unified in the sense that results from one branch of mathematics can be used in another.
Traditional proof-oriented geometry courses in the U.S.A. began by noting that point, line, and plane are three terms that are undefined because we cannot define all terms without having circular definitions. In place of definitions, certain postulates are asserted that implicitly define what point, line, and plane can be; postulates such as “there is exactly one line through two points” and “given a point and a line, there is exactly one line containing that point and parallel to the given line.” To most teachers and students having undefined terms seems to be a weakness. But when integrating algebra into a geometry course, it becomes a strength.
UCSMP Geometry (Coxford, Hirschhorn & Usiskin, 1991; Usiskin et al., 1997; Benson et al., 2009) begins with the geometric view of points and lines, in which, from postulates such as “Through two different points there is exactly one line.” students are led to think that a point stands for a location on a flat surface and lines are extensions of what we draw with rulers. But then, in the next lesson, we note that the same postulates cover a geometry in which a point is an ordered pair of real numbers and a line is the set of ordered pairs that satisfy an equation of the form . In this way, from the very beginning of the geometry course, we justify the use of synthetic non-numeric methods as well as analytic or coordinate geometry throughout. This approach takes advantage of the beauty of deduction as well as the beauty of the unity of mathematics and it enables algebra and geometry to be employed side-by-side in all the later courses.
The Beauty of Connections
xiii
Based on the discussions of the advisory panel, we decided that the last two courses should have two themes apiece: functions and statistics for the 11th grade course, and precalculus and discrete mathematics for the 12th grade course. Trigonometry was added to the title of the first of these courses to make the text adoptable in districts that required a trigonometry course.
With statistics as a “passenger” in the algebra course, and functions and statistics as major themes in the
11th grade course, we found many ways in which ideas from one of these themes were related to ideas in
the other. For instance, the sigma notation used in series was introduced by the need to sum data to calculate
simple statistics as early as the first algebra course. In the UCSMP 11th grade course, we were able to
discuss the translation images of graphs of functions and relations alongside adding or subtracting a constant from
all items in a data set in order to set the mean at 0. We could discuss scale transformations of graphs along with
scaling data when we wished to normalize that data to have a standard deviation of 1. Table 6 shows these and other
ways in which we use topics from statistics to motivate or apply traditional mathematics topics.
The last UCSMP course was meant to combine the precalculus topics needed for success in calculus with the discrete mathematics that would be useful in computer science. Thus we added a year to the standard academic school curriculum, but we started concentrated study of algebra a year earlier than was typical. By having precalculus and discrete mathematics as the two main themes of our 12th grade course, we were able to connect ideas that are usually separated. For instance, we were able to apply ideas from formal logic to explain why solving some equations leads to what are called extraneous solutions. We could discuss factoring of integers alongside factoring of polynomials, prime integers alongside prime polynomials, least common multiples of integers alongside least common multiples of polynomials, and so on. And we could bring together ideas from this course with ideas from all our prior courses.
In 1623, when Galileo wrote in his book Il Saggiatore (“The Assayer”) that the universe is written in the language of mathematics, he was part of a pioneering movement to adopt what we call today the scientific method. One of the purposes of school mathematics is to familiarize students with that language, but what is not appreciated enough is that the language of mathematics can take on many forms, and it is necessary to teach students how to move from one form to another. The opportunity to design multi-year curricula provided the luxury of being able to discuss the same idea in quite different ways, to provide some beautiful mathematical connections.
Consider the notion of successive turns about a point. The evolution begins in the early grades with a physical
turning that we might measure in degrees or revolutions, and we add those measures to get the result. Rotations
about a point in the plane are a mathematical model of the physical action. In geometry, when we discuss what is
sometimes called “angle addition” or an “adjacent angle property”, we typically sweep our hands to connect with a
physical action even though Euclidean geometry is static – the figures do not move. In the coordinate plane, we can
represent a rotation about the origin by a 2 x 2 matrix, and successive rotations by matrix multiplication. When we
write the rotations of magnitudes x and y in matrix form as in Figure 5 and multiply the
matrices, we obtain the formulas for cos(x + y) and sin(x + y) in one line. In fact, we get each
formula twice. It’s beautiful mathematics.
Because there is far more good and accessible mathematics for students than we can fit into the school mathematics
curriculum, if we were only using matrices in this setting, it would not be economical to take the time to develop
the machinery necessary to show the elegant derivation of the formula for Rx that is used in Figure 5.
However, matrices have many more applications than this one – to understanding other transformations, to solving
systems of equations, to networks and Markov chains.
An Elegant Theory of Mathematical Understanding
xiv
In an ICME plenary talk in 2008, Jeremy Kilpatrick noted “mathematics education is not like other scientific fields” (Artigue & Kilpatrick, 2008). He cited a statement in Felix Klein’s Erlangen address in 1872 that
“Each mathematical generation builds on the accomplishments of its predecessors, whereas in other fields [including
mathematics education] it often happens that the old buildings are torn down before the new construction can
proceed.”
Jeremy noted that “We do not always start completely from scratch, but we do a lot of demolition as well of construction.”
However, I believe that there is a space between mathematics and mathematics education that does have eternal truths. In that space is our quest for having students “understand” the mathematics that they are learning. For the UCSMP materials, that understanding is treated overtly and involves four dimensions (Usiskin, 2015):
- a skill-algorithm dimension that ranges from the rote application of an algorithm to the study of algorithms and the invention of new algorithms;
- a property-proof dimension that ranges from rote justification of properties through the writing of proofs and the discovery of new properties;
- a use-application dimension that ranges from the simplest uses known to everyone, to the use of known mathematical models and then the invention of new ones; and
- a representation-metaphor dimension that ranges from repeating known pictures of mathematical ideas to the invention of new representations.
Such a multi-faceted view of understanding is required because to different people, each one of these dimensions dominates the other three in importance. The proverbial “average person on the street” tends to think that you understand mathematics if you know how to get answers to mathematical questions. Mathematicians tend to view a person as understanding mathematics if the person can refer to the properties that explain the mathematics being dealt with. Engineers tend to believe that you don’t really understand mathematics until you can apply the mathematics to real situations. And many psychologists think that real understanding means being able to represent the mathematics in some way, perhaps by a metaphor. These four dimensions are all found in the teaching and learning of mathematics and are remarkably independent of each other. That is why I call them dimensions. For virtually every concept in the UCSMP curriculum, in our lessons and our tests, we strive to have students become acquainted with all four dimensions. Additionally, there is at least one other dimension to the understanding of mathematics – the historical-social dimension – how mathematics evolved and is influenced by social forces; this way is typically ignored in classrooms.
One consequence of the multi-dimensional view of understanding is that we were constantly drawn into geometrical representations of numerical and algebraic ideas and into algebraic representations of geometrical ideas. Thus, this approach to understanding helped us to take advantage of the overall unity of mathematics. And, though it seems to be a complicated view of understanding, there is a sense in which it is an elegant structure for a very inelegant reality.
After a while, we began to realize that our authors tended to prefer one or two of the dimensions of understanding of mathematics over the others. When writing prose and problems, some tended to be focused on skills, some on the mathematical properties, some on applications, some on representations, and some on the historical-social dimension. We took these strengths into consideration when constructing our writing teams, and I think it enriched our materials.
The Writing Teams and the Writing Process
xv
Developing good curriculum requires not only a knowledge of mathematics, but the ability to write clear and interesting material. From the start, talented people contributed to the writing of the UCSMP texts (see UCSMP References at end of this paper). After I wrote the first draft of Transition Mathematics, four very smart and experienced local teachers edited the materials. For each of the other courses, we selected experienced authors as team leaders. John McConnell was the mathematics department head at a local high school and had received his doctorate in mathematics education from Northwestern University studying relationships among teachers and students in 9th-grade algebra (McConnell, 1978). He became our algebra team head. Sharon Senk, as a high school teacher in Newton, Massachusetts, had taught geometry and advanced algebra in tandem to students. Also, in the van Hiele study, she had studied the performance of students on proof (Senk, 1985). She agreed to head the advanced algebra team. To fill out the algebra teams, we advertised nationally, had candidates send in writing samples, and then brought in finalists to judge their ability to work with a team to plan and write on the spot. We obtained some gifted authors by that means. For geometry, I was able to convince Art Coxford to go at it again.
For the last two courses, two individuals shared the leadership. For the course we originally called Functions and Statistics and now call FST, we had Rheta Rubenstein, then a teacher in the Detroit Public Schools, who had been a wonderful author on our Advanced Algebra team, and Jim Schultz, a professor at Ohio State University (later to move to Ohio University), who had already written a wonderful mathematics text for elementary school teachers (Schultz, 1977). For Precalculus and Discrete Mathematics, we convinced two mathematicians, Tony Peressini and Susanna Epp to be co-heads. Tony took the lead on the precalculus parts while Susanna took time from writing a college-level discrete mathematics textbook (Epp, 1990) to take the lead on the discrete mathematics lessons.
Except for FST, which was mostly written away from the university, the writing teams worked 6 to 8 weeks in the summer, 5 days a week, in a single room large enough to house them with one or two student editors and reference materials. Planning meetings were constant. I tried to be at every planning meeting and I was final editor on every lesson. Apparently, I was a tough editor. A few years ago, at a “roast” following a dinner in my honor, some authors prepared a skit about my editing. In the skit, one of the authors jumps for joy when she sees that a word she wrote has survived my editing – the word “the”.
After the algebra texts were written, we realized that our doctoral student editors (Dan Hirschhorn, Dora Aksoy, Jim Flanders, Barry Kissane, Jeff Birky, and Greg McRill) were doing a great deal of author work, and we felt it appropriate to identify them as authors. They were assisted by other students at the University who proofread text and provided answers and solutions to problems. Students at the university were also our production people who took handwritten text and put it in book-read form so that the materials could be tested with more and more students. Over the years we hired over 200 University of Chicago students as editorial or production assistants.
Our field test versions were black-and-white soft-cover or spiral-bound editions. For the first two editions, that work was directed by Susan Chang. For the third edition, the director was Ben Balskus. When our books became commercially published, the production into a hard-cover full-color edition and the accompanying teacher’s edition was done by our publishers. But there was an exception – under Ben’s direction we did the commercial production for the last two books of our third edition ourselves. To have editors in rooms adjacent to the final production was exceedingly efficient and we believe unprecedented.
Large research studies of our materials also had to be managed. At first, Larry Hedges and Susan Stodolsky directed our summative research studies. After a few years it became clear to us that our desire for independent evaluators within UCSMP left us without some kinds of data that we dearly wanted. For instance, we were very interested in the effects of calculators on student learning, but the evaluators thought this was a minor issue. As a result, Sharon Senk and I shared most of the work on the later evaluations of the first edition. Then Denisse Thompson, who had started with us by being selected in the competition for authors and later became a doctoral student, decided to use the testing of Precalculus and Discrete Mathematics for her doctoral dissertation, and then became director of our research (Thompson, Senk, et al., multiple years).
The first edition was finished in 1991 and the sales caused our publisher to ask us to begin work immediately on a second edition. For the second edition we invited back many of our first edition authors and repeated the competition to fill out the author teams. Two new names appear on three books apiece: David Witonsky, an editor, and Nils Ahbel, a high school teacher who since that time for many years has been the department head at the Deerfield Academy, a private school in Massachusetts. Nils embodies a principle that has been repeatedly confirmed over the years, namely that there are in our schools some mathematics teachers whose knowledge and abilities regarding school mathematics are the equals of any university professors in our field. The second edition was done by 1997.
For the third edition, we switched publishers and worked from 2005 to 2010. We also added a course to precede Transition Mathematics to reflect changes in the U.S.A. to a middle school concept for grades 6 to 8. Of extreme importance among the many authors of this edition was Natalie Jakucyn, who came to us as an experienced teacher who helped to edit the first edition of Advanced Algebra. For the second edition she was in charge of the editing of the manuscript for each book. She then went back to teaching full-time but returned to head the writing of the third edition and more recently, she headed the work in creating a digital platform for the seven third edition books.
Finally, it is important to acknowledge that a project of this size requires an administration team. Carol Siegel, our office manager for three decades, managed five of the seven international conferences UCSMP has hosted at the University of Chicago since 1985, including the two most recent under the auspices of the NSF-supported Center for the Study of Mathematics Curriculum. She also helped screen all applicants for editorial and production positions with UCSMP, and due to her and other administrative staff, we continually assembled an extraordinarily nice support team for our writing, editing, and production efforts.
Further details regarding the design and development of curricular materials before and within the University of Chicago School Mathematics Project can be found in UCSMP Newsletters 1-40 online at http://ucsmp.uchicago.edu/newsletters, as well as in Usiskin (2003); Usiskin (2007), and Reys & Reys (2014).
Summary and Acknowledgements
xvi
In this paper I have attempted to describe some of the detailed thinking and work that went into designing the UCSMP curriculum. In virtually every case, we were not the pioneers. People before us were designing curriculum involving applications and modeling, involving transformations, involving statistics and discrete mathematics, using the latest in technology, and working for understanding in mathematics. At Chicago I had an unusual opportunity given to few people – to organize and lead a team to design and write a complete mathematics curriculum for secondary schools. That work would not be known today were it not for the fact that many others throughout the world were working to achieve the same goals – to create a relevant, teachable and learnable mathematics curriculum for the vast majority of students.
Our work in elementary schools was influenced by our translations of Soviet textbooks (Moro & Bantova, 1992; Moro, Bantova & Beltyukova, 1992; Pcholko, Bantova, Moro & Pyshkalo,1992; Usiskin, 1997). That we could raise expectations in middle schools was influenced by our translations of Japanese textbooks (Kodaira, 1992), by materials from Bryan Thwaites and Geoffrey Howson of SMP in the U.K., by the work of Hans Freudenthal and later the Freudenthal Institute, by Sol Garfunkel at COMAP, and by Mogens Niss and Werner Blum and the ICTMA people working in mathematical modeling and applications, by Jim Fey and Kathy Heid’s pioneering work in computer algebra systems, by Jean-Marie Laborde and Nick Jackiw’s work in dynamic geometry, and by Texas Instruments and Casio’s work in creating usable and inexpensive technology for schools.
Even with all this guidance, we could not do any of this work without the support of hundreds of school administrators and teachers in our formal studies and thousands of teachers willing to teach materials significantly different from those they had seen or taught from previously.
It is wonderful that we have a world-wide community dedicated to the improvement of the curricular experiences that we afford to students. But we should not get complacent. After a period of wonderful mathematics curriculum development in the U.S.A. in the 1990s that stretched into the 2000s, there is now basically no curriculum development in the U.S.A. The Common Core has killed mathematics curriculum development here. not only with its back-to-basics regressive content but also with the creation of a megalithic testing structure that will make future changes difficult to implement. We need to celebrate our successes, but we need to be wary of those who wish to dictate their view of education as if it is the only way to go.
References
xvii
Beberman, M. (1958). An Emerging Program of Secondary School Mathematics. The 1958 Inglis Lecture. Cambridge, MA: Harvard University Press.
Beberman, M. & Vaughan, H.E. (1964). High School Mathematics, Course 1. Boston: D.C. Heath.
Bell, M.S. (1972). Mathematical Uses and Models in Our Everyday World. Studies in Mathematics, Volume XX. Stanford, CA: School Mathematics Study Group.
Benson, J., Klein, R., Miller, M.J., Cappuzzi-Feuerstein, C., Fletcher, M., Marino, G., Powell, N., Jakucyn, N. & Usiskin, Z. (2009). UCSMP Geometry. Third Edition. New York: Wright Group/McGraw-Hill.
Carpenter, T.P., Moser, J.M. & Romberg, T.A. (1982). Addition and Subtraction: A Cognitive Perspective. Hillsdale, J: Lawrence Erlbaum.
Coxford, A.F. & Usiskin, Z. (1971). Geometry - A Transformation Approach. River Forest, IL: Laidlaw.
Coxford, A.F. & Usiskin, Z. (1972). A Transformation Approach to Tenth–Grade Geometry. The Mathematics Teacher 65:1, pp. 21-30. Reprinted in We Need Another Revolution: Five Decades of Curriculum Papers by Zalman Usiskin. (2014). Reston, VA: NCTM, pp. 292-302.
Coxford, A.F., Hirschhorn, D. & Usiskin, Z. (1991). UCSMP Geometry. Glenview, IL: Scott, Foresman.
Epp, S.S. (1990). Discrete Mathematics with Applications. Belmont, CA: Wadsworth.
Euler, L. (1972). Elements of Algebra. Translated by J. Hewlett. New York: Springer.
Hardy, G.H. (1940). A Mathematician’s Apology. Cambridge: Cambridge University Press.
Heath, T.L. (1956). The Thirteen Books of Euclid’s Elements. New York: Dover.
Henderson, K.B., Usiskin, Z. & Zaring, W. (1971). Precalculus Mathematics. New York: McGraw-Hill.
Jacobs, H. (1971). Mathematics – A Human Endeavor. Boston: W.H. Freeman.
Kinsella, J.J. (1965). Secondary School Mathematics. New York: The Center for Applied Research in Education, Inc.
Kodaira, K. (Ed.) (1992). Japanese Grade 7 Mathematics. Japanese Grade 8 Mathematics. Japanese Grade 9 Mathematics. Translated by H. Nagata. Chicago: UCSMP.
McConnell, J.W. (1978). Relationships among High-inference Measures of Teacher Behaviors and Student Achievement and Attitude in Ninth Grade Algebra Classes. Unpublished PhD dissertation, Northwestern University.
Moro, M.I. & Bantova, M.A. (1992). Russian Grade 2 Mathematics. Translated by R.H. Silverman. Chicago: UCSMP.
Moro, M.I., Bantova, M.A. & Beltyukova, G.V. (1992). Russian Grade 1 Mathematics. Translated by R.H. Silverman. Chicago: UCSMP.
National Governors Association Center for Best Practices, Council of Chief State School Officers. (2010). Common Core State Standards: Mathematics. Washington D.C.: National Governors Association Center for Best Practices, Council of Chief State School Officers.
Pcholko, A.S., Bantova, M.A., Moro, M.I. & Pyshkalo, A.M. Russian Grade 3 Mathematics. Translated by R.H. Silverman. Chicago, UCSMP, 1992.
Reys, B. & Reys, R. (Eds.) (2014). We Need Another Revolution: Five Decades of Curriculum Papers by Zalman Usiskin. Reston, VA: National Council of Teachers of Mathematics.
Rubenstein, R. N, Schultz, J.E, Senk, S., Hackworth, M., McConnell, J. & Viktora, S. (1992). UCSMP Functions, Statistics, and Trigonometry. Glenview, IL: Scott Foresman.
Schultz, J. E. (1977). Mathematics for Elementary School Teachers. Columbus, OH: Charles Merrill.
Senk, S. (1985). How Well Do Students Write Geometry Proofs? The Mathematics Teacher 76(6), pp. 448-456.
Stigler, J.W., Fuson, K.C., Ham, M. & Kim, M.S. (1986). An Analysis of Addition and Subtraction Word Problems in American and Soviet Elementary Textbooks. Cognition and Instruction 3(3), pp. 153-171.
Suydam, M.N. (1976). Electronic Hand Calculators: The Implications for Pre-College Education. Washington, DC: National Science Foundation.
Thorndike, E.L, Cobb, M. V., Orleans, J. S., Symonds, P. M., Wald, E. & Woodyard, E. (1923). The Psychology of Algebra. New York: Macmillan.
Troelstra, R., Habermann, A.N., deGroot, A. & Bulens, J. (1965). Transformatiemeetkunde 1-3. Groningen, Netherlands: J. B. Wolters.
University of Chicago School Mathematics Project (UCSMP). (2016). Everyday Mathematics. Grades PreK-6. 4th Edition. New York: McGraw-Hill.
University of Illinois Committee on School Mathematics (UICSM). (1959). High School Mathematics, Courses 1-4. Urbana, IL: University of Illinois Press.
Usiskin, Z. (1972). The Effects of Teaching Euclidean Geometry via Transformations on Student Achievement and Attitudes in Tenth-Grade Geometry. Journal for Research in Mathematics Education 3(4), pp. 249-259.
Usiskin. Z. (1975). Advanced Algebra with Transformations and Applications. River Forest, IL: Laidlaw.
Usiskin, Z. (1979). Algebra Through Applications with Probability and Statistics. Reston, VA: National Council of Teachers of Mathematics.
Usiskin, Z. (1997). Doing Algebra in Grades K-4. Teaching Children Mathematics 3(6), pp. 346-356.
Usiskin, Z. (2003). A Personal History of the UCSMP Secondary Curriculum. In G.M.A. Stanic & J. Kilpatrick (eds.), A History of School Mathematics. Reston, VA: NCTM, pp. 673-736.
Usiskin, Z. (2007). The Case of the University of Chicago School Mathematics Project – Secondary Component. In C.R. Hirsch (ed.), Perspectives on the Design and Development of School Mathematics Curricula. Reston, VA: NCTM, pp. 173-182.
Usiskin, Z. (2015). What Does It Mean to Understand Some Mathematics? In Je, C.S. (Ed.), Selected Regular Lectures from the 12th International Congress on Mathematical Education. Springer, pp. 821-842.
Usiskin, Z., Hirschhorn, D.B., Highstone, V., Lewellen, H., Oppong, N., DiBianca, R. & Maeir, M. (1997). UCSMP Geometry. Second Edition. Glenview, IL: Scott Foresman.
Wallis, W.A. & Roberts, H.V. (1954). The Nature of Statistics. New York: W.W. Norton.
Yates, D.S., Moore, D.S. & Starnes, D.S. (2003). The Practice of Statistics. New York: W.H. Freeman.
Appendix A. UCSMP Texts for Secondary Schools (grades 6-12)
xviii
First edition (commercial publication Glenview, IL: Scott Foresman)
Transition Mathematics. Zalman Usiskin, James Flanders, Cathy Hynes, Lydia Polonsky, Susan Porter, and Steven Viktora. Field test versions 1983-85; Field test hardcover version 1986; Scott, Foresman editions 1990, 1992
Algebra. John W. McConnell, Susan Brown, Susan Eddins, Margaret Hackworth, Leroy Sachs, Ernest Woodward, James Flanders, Daniel Hirschhorn, Cathy Hynes, Lydia Polonsky, and Zalman Usiskin. Field test versions 1985-88; Scott, Foresman editions 1990, 1993
Geometry. Arthur F. Coxford, Jr., Daniel Hirschhorn, and Zalman Usiskin. Field test versions 1986-89; Scott Foresman editions 1991, 1993
Advanced Algebra. Sharon L. Senk, Denisse R. Thompson, Steven S. Viktora, Rheta Rubenstein, Judy Halvorson, James Flanders, Cathy Hynes, Natalie Jakucyn, Gerald Pillsbury, and Zalman Usiskin. Field test versions 1985-88; Scott, Foresman editions 1990, 1993
Functions, Statistics, and Trigonometry. Rheta N. Rubenstein, James E. Schultz, Sharon L. Senk, Margaret Hackworth, John W. McConnell, Steven S. Viktora, Dora Aksoy, James Flanders, Barry Kissane, and Zalman Usiskin. Field test versions 1986-89; Scott, Foresman edition 1992
Precalculus and Discrete Mathematics. Anthony L. Peressini, Susanna S. Epp, Kathleen A. Hollowell, Susan Brown, Wade Ellis, Jr., John W. McConnell, Jack Sorteberg, Denisse R. Thompson, Dora Aksoy, Geoffrey D. Birky, Greg McRill, and Zalman Usiskin. Field test versions 1987-90; Scott Foresman edition 1992
Second edition (commercial publication Glenview, IL: Scott Foresman and Scott Foresman – Addison Wesley, and Upper Saddle River, NJ: Prentice-Hall)
2
Transition Mathematics. Zalman Usiskin, Cathy Hynes Feldman, Suzanne Davis, Sharon Mallo, Gladys Sanders, and David Witonsky. Test version 1992-93; Scott Foresman edition 1995; Scott Foresman – Addison Wesley edition 1998; Prentice Hall edition 2002
Algebra. John W. McConnell, Susan Brown, Sharon L. Senk, Ted Widerski, Scott Anderson, and Zalman Usiskin. Test version 1992-93; Scott Foresman edition 1996, Scott Foresman – Addison Wesley edition 1998; California edition, 2000; Prentice Hall edition 2002
Geometry. Zalman Usiskin, Daniel B. Hirschhorn, Virginia Highstone, Hester Lewellen, Nicholas Oppong, Richard DiBianca, and Merilee Maeir. Test version 1993-94; Scott Foresman edition 1997; Prentice Hall edition 2002
Advanced Algebra. Sharon L. Senk, Denisse Thompson, Steven S. Viktora, Zalman Usiskin, Nils P. Ahbel, Suzanne Levin, and Marcia Weinhold. Test version 1993-94; Scott Foresman edition 1996; Prentice Hall edition 2002
Functions, Statistics, and Trigonometry. Sharon L. Senk, John W. McConnell, Steven S. Viktora, Zalman Usiskin, Nils P. Ahbel, Virginia Highstone, and David Witonsky. Scott Foresman - Addison Wesley 1997
Precalculus and Discrete Mathematics. Anthony L. Peressini, John W. McConnell, Zalman Usiskin, Nils P. Ahbel, and David Witonsky. Scott Foresman - Addison Wesley 1998
Third edition (commercial publication Chicago: Wright Group/McGraw-Hill; Chicago: UChicagoSolutions)
3
Pre-Transition Mathematics. John W. McConnell, Cathy Hynes Feldman, Deborah Heeres, Emily Kallemeyn, Enrique Ortiz, Noreen Winningham, Karen Hunt, Troy P. Regis, Mihaela Florence Singer, John Wolfe, Natalie Jakucyn, and Zalman Usiskin. Field test version 2006-07; Wright Group/McGraw-Hill edition 2009
Transition Mathematics. Steven S. Viktora, Erica Cheung, Virginia Highstone, Catherine Capuzzi, Deborah Heeres, Neva Metcalf, Susan Sabrio, Natalie Jakucyn, and Zalman Usiskin. Field test version 2005-06; Wright Group/McGraw-Hill edition 2008; UChicagoSolutions edition 2016
Algebra. Susan Brown, R. James Breunlin, Mary H. Wiltjer, Katherine M. Degner, Susan K. Eddins, Michael Todd Edwards, Neva Metcalf, Natalie Jakucyn, and Zalman Usiskin. Field test version 2005-06; Wright Group/McGraw-Hill edition 2008
Geometry. John Benson, Ray Klein, Matthew J. Miller, Catherine Capuzzi-Feuerstein, Michael Fletcher, George Marino, Nancy Powell, Natalie Jakucyn, and Zalman Usiskin. Field test version 2006-07; Wright Group/McGraw-Hill edition 2009; UChicagoSolutions edition 2016
Advanced Algebra. James Flanders, Marshall Lassak, Jean Sech, Michelle Eggerding, Paul J. Karafiol, Lin McMullin, Neal Weisman, and Zalman Usiskin. Field test version 2006-07; Wright Group/McGraw-Hill edition 2009; UChicagoSolutions edition 2016
Functions, Statistics, and Trigonometry. John W. McConnell, Susan A. Brown, Paul J. Karafiol, Sara Brouwer, Mary Ives, Rosa McCullagh, Natalie Jakucyn, and Zalman Usiskin. Field test version 2007-08; Wright Group/McGraw-Hill edition 2010; UChicagoSolutions edition 2016
Precalculus and Discrete Mathematics. Anthony L. Peressini, Peter D. DeCraene, Molly A. Rockstroh, Steven S. Viktora, Ward E. Canfield, Mary Helen Wiltjer, and Zalman Usiskin. Field test version 2007-08; Wright Group/McGraw-Hill edition 2010; UChicagoSolutions edition 2016
About the Author
xix
Zalman Usiskin is a professor emeritus of education at the University of Chicago and the overall
director of the University of Chicago School Mathematics Project. His research and interests cover all aspects of
mathematics education, with particular emphasis on curriculum, instruction, and testing; the history of mathematics
education; and educational policy. He received the Glenn Gilbert National Leadership Award from NCSM in 1994, and a
Lifetime Achievement Award from NCTM in 2001, the first person to receive both awards. In 2014, NCTM published a book of
38 of his papers, the first time that the organization published a collection of writings of one individual.
In 2017, Zalman Usiskin was awarded the
ISDDE Prize for Lifetime Achievement.