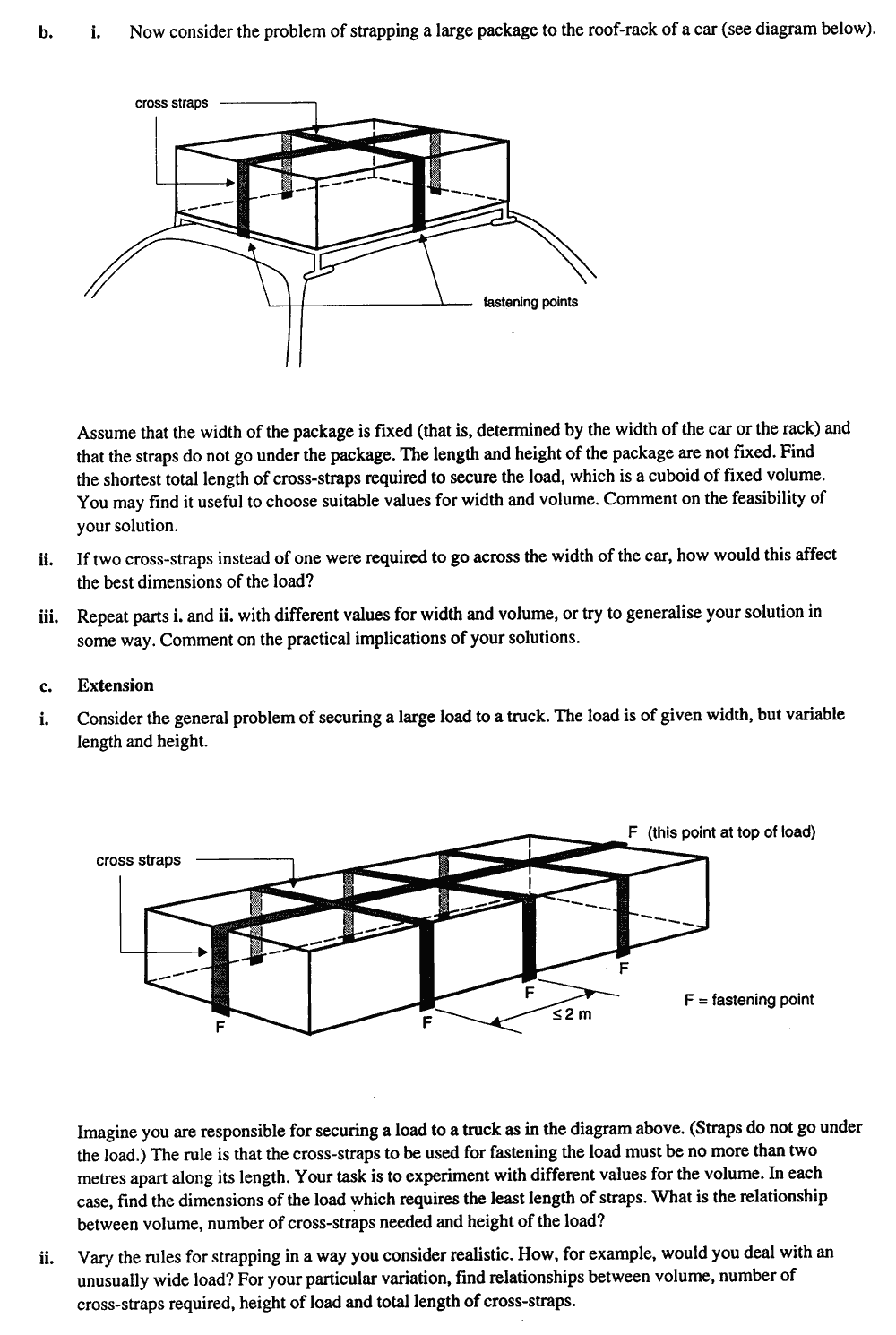
On Strategic Design
Hugh Burkhardt
Abstract
i
This paper develops the concept of “strategic design”, the design implications
of the interactions of a product with the whole user system, and relates
it to other aspects of design. It describes some examples of poor strategic
design that occur frequently, and some cases where effective strategic
design has been important in the large-scale impact of an ambitious educational
innovation. From these, the paper then seeks to infer some principles for
strategic design. It is aimed at the three major constituencies of ISDDE:
designers, design team leaders, and the client-funders that often commission
their work. The hope is that sharpened awareness of the importance, and
the challenges, of strategic design may help to increase the impact of
good design as a whole.
The goals of this paper are to:
- Articulate and illustrate the concept of “strategic design”;
- Relate it to other aspects of design;
- Pursue some of the issues it raises; and
- Suggest some principles for strategic design.
I will start with a working description:
Strategic design focuses on the design implications of the interactions
of the products, and the processes for their use, with the whole user system
it aims to serve.
The importance of strategic design is illustrated by the many examples of
design excellence that have been undermined by poor strategic design – wonderful
lessons, assessment tasks, and professional development activities that are
never seen, while mediocrity
(and worse) is widespread.
Section 1 outlines the concept, which will be developed throughout the paper,
distinguishing strategic, tactical and technical design.
Section 2 illustrates the concept with three areas of poor strategic design
that are commonplace across education systems, and the design challenges
each presents. Section 3 sets out to identify underlying causes of poor strategic
design, and the contributions to it of client-funders, education professionals,
and poor methodology. Switching to a more upbeat note, Section 4 describes
four projects that paid close attention to strategic design and that have
had substantial impact on the systems they aimed to improve. The final sections
set out some principles for strategic design, issues that need further study,
long and medium term goals, and immediate actions that can forward their
achievement.
1. Aspects of educational design
1
I choose here to distinguish three major aspects of educational design – strategic,
tactical and technical – if
only to make clear what strategic design is not. (Illustrative
examples are given in parentheses below.)
Technical design is the detailed process with which any designer
is familiar. It is focused on the design of individual elements of the product
(e.g. a teaching unit; a professional development module; an assessment task).
Technical design is focused on the end users and their environment (students
and the teacher in classrooms; teachers in professional development activities;
the diverse students taking a test, and those who will score their responses).
Technical design is the responsibility of the lead designer of
the unit.
Tactical design is focused on the overall internal structure
of the product (e.g. a multi-year set of teaching materials; a year’s assessment;
a professional development package). Typically it involves such things as:
- Specification of core design principles, selected in the light of prior
research on learning, teaching, and/or professional development trajectories
– or, too often, just marketing;
- Selection of specific learning and performance goals, including strands
of progression;
- Specifying sequences and cross-connections within the materials, balancing
linear coherence with diverse multiple connections (among concepts and
contexts, standard results to learn and open investigations to experience).
Tactical design is a responsibility of the design team leaders
and lead designers, working with their colleagues in the design team.
Strategic design, the focus of this paper, is concerned
with the overall structure of the product set and how it will relate to the
user-system. It applies in different forms to most of the products and processes
that educational designers tackle: curriculum specifications; assessment;
teaching materials; professional development processes and materials; building
system capacity in various ways. Typically strategic design involves not
simply the end-users (e.g. teachers and their students) but all the key communities
involved who will affect decisions on the framework within which the users
work – school leadership; school system leadership; politicians; parents;
and various other professions, such as assessment designers and researchers.
Strategic design includes such things as:
- Identifying a specific opportunity for improvement;
- Selecting a set of improvement goals;
- Designing the overall structure of a set of tools that can forward them;
- Choosing or designing a model of change (whether, for example, comprehensive
or more specific; one-step or gradual; curriculum-led, assessment-led,
or professional development led) along with the phases, pacing and timing
of implementation;
- Identifying the resources that are needed to do the job well (how much
design effort, trialling, implementation support, and of what kinds), and
the compromises that are acceptable;
- Recognizing and questioning constraints from the client’s grand strategy (generic
performance goals; alignment; model of change; top-down v proposal driven);
and
- Advising the client on the likely implications of their various decisions,
including their likely unintended consequences and uncertainties – and
suggesting changes.
Strategic design is a responsibility of the design team leadership,
usually in negotiation with the client-funder – often government, a quasi-government
agency, or a foundation.
There is no hierarchy of importance among strategic, tactical and technical
design. While this paper focuses on strategic design, all three are important
if the product is to work well. All three offer opportunities for creativity
in the search for excellence – and for making ghastly choices that undermine
the whole enterprise.
My own view is that poor strategic design is the most common cause
of failure, while excellence in technical design is the
main source of the magic combination of power, surprise and
delight that characterizes really outstanding products –
as in music, art and literature, details matter. Tactical design is
central to the coherence of the enterprise.
This framework complements Goodlad’s (1994) rather different analytic perspective
on curriculum design, which distinguishes:
- The socio-political perspective – the influence exercised by
various individual and organizational stakeholders;
- The technical-professional perspective – the methods of the
curriculum development process;
- The substantive perspective – the question of what should be
learned.
This paper suggests that 1 must be part of 2, explicitly seen as part of
the design and development process and proactively addressed as such.
Design control is the other concept that belongs here.
How are design decisions made, and by whom? While all members of a design
team will contribute ideas and suggestions on all three aspects of design,
it is worth identifying how choices are made among the huge range
of possibilities that any design task affords. The obvious principle is to
make the best use of the diverse design talent available in the team. This
hierarchy of decision taking will influence the design and its impact.
There are various approaches to design control. Some small teams work by
consensus – this has obvious advantages but can lead to long unproductive
discussions and suboptimal compromises.
In contrast, as in architecture, design control may rest with a single lead
designer – or, sometimes, a small group who have worked closely together
for a long time. Alternatively, different people may have design control
over different aspects of the design, reflecting their strengths – e.g. as
strategic, tactical or technical designers, as software designers, or in
relation to specific learning goals.
Whatever the choice, I have found that it is important to make clear the
locus of design control – this smooths and speeds the design process, while
leaving most room for individual design flair.
2. Common failures in strategic design
2
More often than not, educational initiatives that seek to improve student
learning fail to achieve their stated goals. This paper makes the case that
this is often, at least partly, due to poor strategic design. This is unsurprising.
Strategic design is often assigned to committees of advisers by the client-funder,
with both seeing it as a policy issue, rather than a design challenge that
may be crucial to the success of the innovation. For government agencies,
ad hoc decisions, dominated by practical policy considerations, are the norm.
If we are to do better, we must understand the phenomena involved. I begin
with some examples, moving on in the next section to look at underlying causes.
Those who seek examples of poor strategic design face un embaras
de richesse. Many initiatives have doom written all over them – predictable,
and often predicted. Some ignore well-known features of the system – for
example, that most teachers teach to the test when high stakes are involved.
Some fail to recognize that a design does not reflect its purpose – for
example, that specifying performance goals involves more than a list of
topics in mathematics or science. Some show no sign of any systematic attempt
to reconcile their usually-ambitious goals with the limitations of the
process chosen for achieving them – for example, that a few sessions of
discussion will not enable teachers to profoundly expand their range of
classroom teaching skills. The following three examples are all repeated
regularly in many countries and school systems. The outline of each that
follows focuses on its strategic design, the form of its failure, and the
design challenges that must be overcome if we are to do better.
2A Assessment – the “only measurement”
fallacy
1
Policy makers in the Anglophone countries and some others are wedded to
using tests of various kinds as prime instruments of system control. Tests
are seen as reliable measures of
student, teacher and school performance, forming the basis of each school’s
“accountability” to the society that funds it. Targets are set in terms of
test scores that have serious consequences for those concerned. Students’
access to higher education depends on their test scores. In England, schools
are ranked on test scores into “league tables” to guide “parental choice”.
Schools that under-perform may be “taken into special measures” or closed.
Similar sanctions apply in the US.
Given the importance of tests, it seems obvious that their design should
be a focus of attention. They should embody the full set of performance goals
in a balanced way. Yet
this central responsibility of test providers and those that commission test
design is widely ignored, and sometimes denied. Their focus is on the statistical
properties of the test and the “fairness” of the procedures, with little
attention to what aspects of performance are assessed.
Policy makers talk and behave as though tests are just “measurement”; they
choose simple tests because they are cheap and, if pressed, argue that the
results correlate with more valid and elaborate assessments. Most articulate
education professionals dislike tests so much that, hoping to marginalize
testing, they make no serious effort to improve the current versions.
This approach ignores two of the three roles that high-stakes assessment inevitably plays.
In brief, it:
- Measures levels of student performance, but only across the
range of task-types used;
- Exemplifies performance objectives – the types of task in high-stakes
tests show what kinds of performance will be recognized and rewarded in
a clear form that teachers and students readily understand; as a result,
this set of task types
- Dominates classroom activities – the task types in high-stakes
tests largely determine the pattern of teaching and learning activities
in most classrooms.
Thus assessment design is the unnoticed “elephant in the room” in the planning
of improvement programs. There is plenty of evidence that “what you test
is what you get” (WYTIWYG) is a fact of life (see e.g. Black
and Atkin 1996, Barnes, Clarke and Stephen 2000). So in systems with high-stakes
assessment, the tests are the de facto standards. While
the UK national inspectors of schools (Ofsted 2006, 2008) remark with regret
on the dominance of test-focused activities, teachers regard it as inevitable
– after all, these are the measures of their performance that society has
decided to value. More hopefully, where balanced high-stakes tests have been
adopted, they have proven to be a powerful influence in improving teaching
and learning in classrooms (see Section 4).
The design challenge
The design of well-balanced assessment in a form that can be used for accountability
purposes has been a solved problem for many years. There are working examples
around the world of high-stakes timed examinations that show what can be
done, and how it can enhance learning. They are not perfect but are vastly
better balanced than most current tests. History contains many outstanding
examinations that enabled students to show what they know, understand
and can do. The
strategic design principle here is to include task types that represent the
full range of performance goals.
The cost and complexity of high-quality balanced assessment is greater than
for machine-marked multiple choice tests; more complex tasks cannot be set
and scored for $1 per student-test, a widely-accepted cost target in the
US. (The massive cost of the class time wasted on otherwise-unproductive
test-prep is generally ignored.)
There are also well-established ways of lowering the cost of assessment
so that it can monitor standards as reliably as at present, while enhancing student
learning. A strategy that has multiple benefits is to make teachers the prime
assessors, providing them with good assessment tools and some training, and
monitoring their scoring on a sampling basis. The many examples of this approach
in practice show that it is also powerful professional development for the
teachers involved. It links naturally to formative assessment in the classroom,
which research shows to be such a powerful way of improving learning (Black
and Wiliam 1998).
Strategically, it is actually unwise to hold costs for structured assessment
down to current levels, well below 1% of the ~$10,000 per student-year that
education typically costs. Feedback is crucial factor in determining the
behaviour of systems of all kinds. Well–structured feedback on student achievement
(Role A above), performance goals (Role B), and exemplar tasks for the classroom
(Role C) are worth far more than the current investments in these areas.
Even when research-based methods of design and development have been used
in assessment, notably in some test development, the commissioning specification
has often been too narrow, excluding design solutions that would allow the
realization of the policy goals. The purely statistical methods used in traditional
psychometrics inevitably move attention from the kinds of performances that
are assessed, which vary from subject to subject, to the statistical properties
of the test.
2
2B How “standards” drive down
standards
3
Many current models of national and state curriculum specifications
(“standards” in what follows) in mathematics and science are examples
of bad strategic design – they have the effect in practice opposite to
that intended. They actually drive down standards of performance in the
subject. In explaining this I shall use as the lead example the National
Curriculum for Mathematics in England. However, many state standards
in the US and elsewhere have much the same structure – and effect.
Criterion referencing is the source of the problem. The National
Curriculum and most current mathematics “standards” in the US were designed
on the principle that achievement goals can be specified through a detailed
list of level criteria – concepts and skills that a student
at that level should know, understand and show in tests. For example:
Use the rules of indices for positive integer values, e.g.
simplify expressions such as 2x2 + 3x2, 2x2 x 3x2,
(3x2)3
From Level 7 of 1988 UK National Curriculum design: Algebra Target 2
(see Figure 1)
Or:
Factor simple quadratic expressions with integer coefficients,
e.g.
x2 + 6x + 9, x2 + 2x – 3, and x2 –
4;
Solve simple quadratic equations, e.g.
x2 = 16 or x2 = 5 (by taking square roots); x2 –
x – 6 = 0, x2 – 2x = 15 (by factoring);
verify solutions by evaluation.
From Michigan Grade Level Content Expectations - Grade 8 Algebra item
A.FO.08.08 (See Figure 2).
Note the brevity of the task examples given.
Criterion referencing is an attractively simple idea. The public
accepts it and policy makers on both sides of the Atlantic seem to love it.
But it is a dangerous illusion. What is the problem? Fundamentally, it is
that:
The level of difficulty of a substantial task depends on various interacting
factors – increasing with the complexity, unfamiliarity, and technical
demand of the task, and the autonomy expected of the student in tackling
it.
Thus the difficulty of the task is higher than that of its technical elements,
tested separately – a rich task that is challenging for a good 16 year-old
student (called level 7) may require only mathematical concepts and skills
that were taught in elementary school (level 4 and below). The “Consecutive
Sums” task is an example.
Consecutive sums
4
The number 9 can be written as the sum of consecutive whole numbers in
two ways:
9 = 2 + 3 + 4
9 = 4 + 5
The number 16 cannot be written as a consecutive sum.
Now look at other numbers and find out all you can about writing them
as sums of consecutive whole numbers.
OK, this seems fairly obvious – but why are criterion-based standards dangerous?
Because, it is only fair to give students the opportunity to meet
the criteria for the highest level they might be able to reach – this is
achieved by testing each concept and skill separately with a short topic-focused
item that has no other cognitive load (from complexity, unfamiliarity,
or longer chains of reasoning) that would increase its difficulty. In the
following task (from Grade 10 GCSE):
(a) Factorise x2 - 10x + 21
(b) Hence solve x2 - 10x + 21 = 0
..note the fragmentation of an already straightforward exercise; this is
done to test explicitly the two criteria:
- Can factorise a quadratic expression
- Can solve a quadratic equation
This approach is the only way that “standards” which define levels through
detailed lists of concepts and skills can be made to work. UK mathematics
tests now consist of that kind of fragmented performance which, because the
stakes are high, also dominates classroom learning activities (Ofsted 2006, 2008) . Clear evidence that such fragmentation is commonplace can be found
by comparing test items with standards, as above.
The damage to student learning is profound. Success with such fragments
has little value outside the mathematics classroom; it surely does not
guarantee success with the more substantial chains of reasoning that
doing and using mathematics involves. To be useful in solving substantial
problems, from the real world or within mathematics, a technique needs
multiple connections in the student’s mind – to other math concepts and
to diverse problem contexts within and outside mathematics. These connections
are built over time, by learning how to tackle more complex tasks like Consecutive
Sums. Such tasks (see Figure 3 for more examples)
are much more challenging than their technical demand suggests because
the strategic demand is a major part of the total cognitive load that
determines difficulty.
To summarise, when "standards" are based on criterion referencing
by topic, the level criteria inevitably (on grounds of fairness) require
short item testing focused on the listed topics, which leads to short
item teaching (via WYTIWYG, explained in section
2A).
This range of task-types covers only a narrow subset of performance goals
that is useless outside schools. This undermines student learning by not
preparing students to think with mathematics about the more substantial
tasks they will meet in life outside the classroom – the epitome of low standards.
The design challenge
How might one design “standards” that set clear learning and performance
goals without narrowing the curriculum? There have been various attempts
at improving criteria to include strategic and tactical skills (often called processes)
at different levels. There is a fundamental problem here too: the same strategies
and tactics help people solve problems across the range of difficulty. Again, it
is tasks, not processes, that have well-defined “levels” of difficulty.
Other countries have taken a quite different approach to the design
of standards in mathematics and science, describing the learning and
performance goals in broad terms. This approach relies on the professional
expertise of teachers and others to find a more detailed realisation
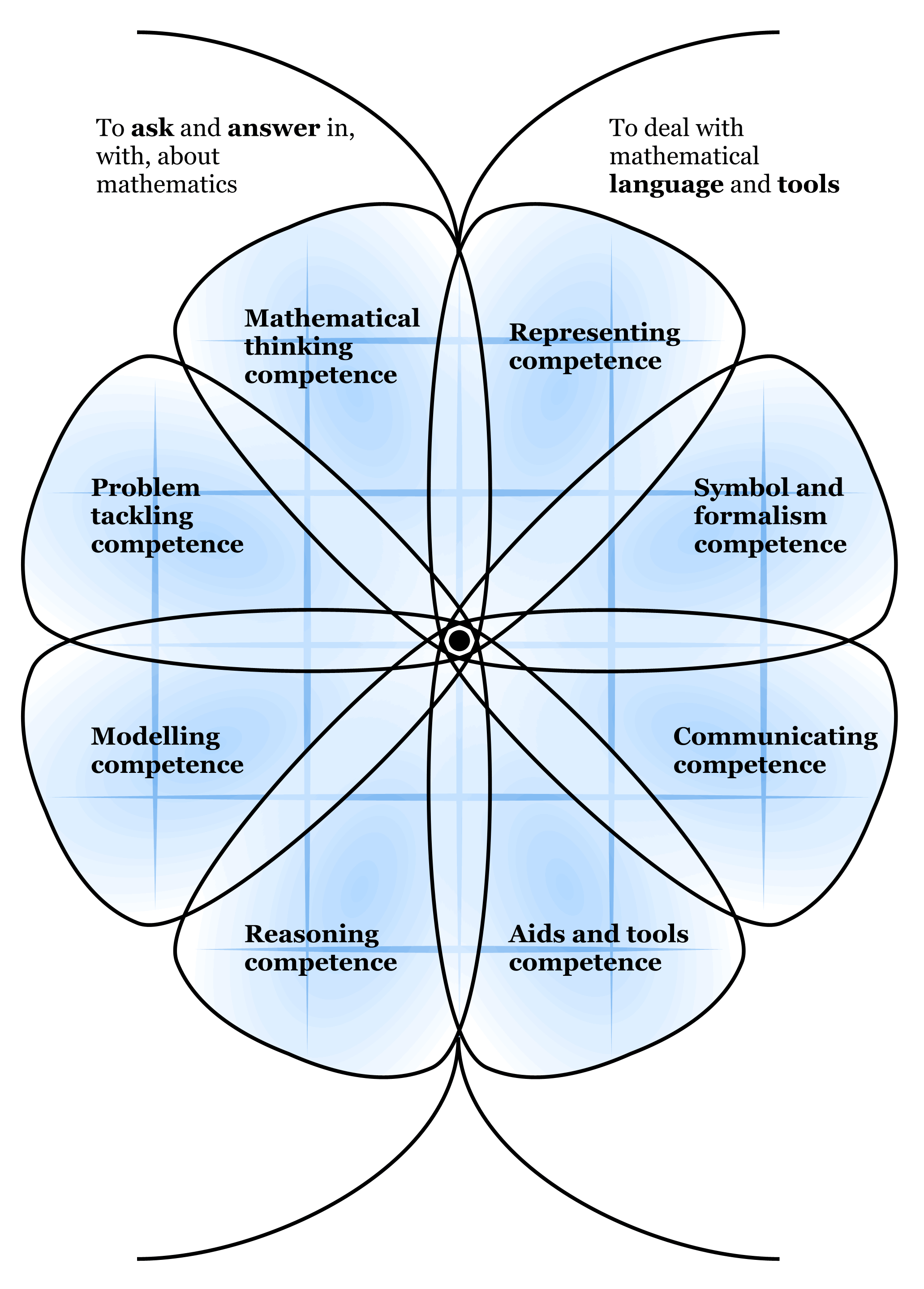
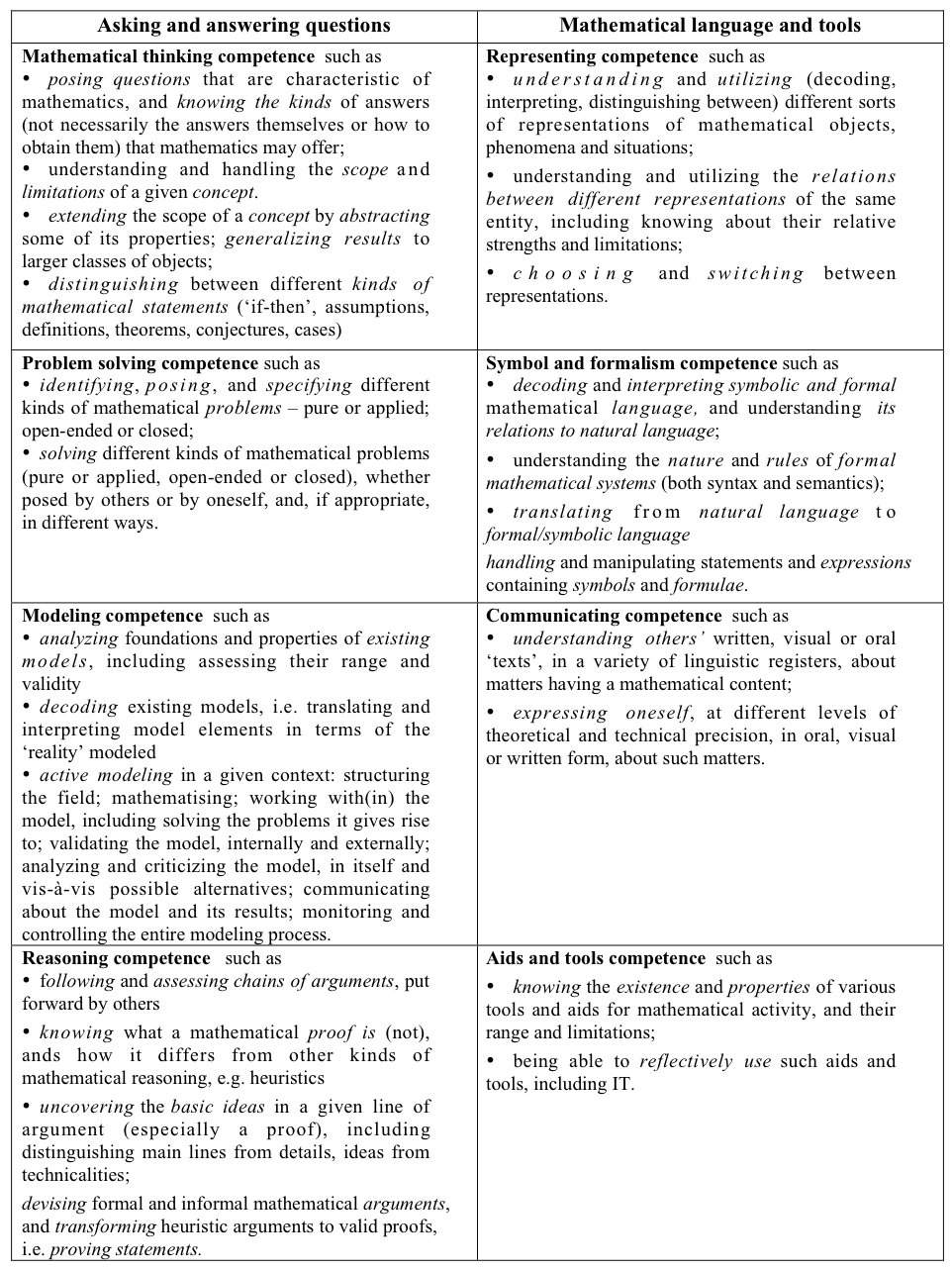
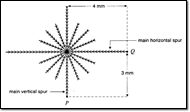
that is appropriate to their local circumstances. The “flower diagram” (Figure
4) used in mathematics standards in Denmark illustrates this approach.
These broad descriptions of competencies do not define levels of difficulty.
So it is not surprising that they are common in school systems that do
not use tests as an accountability tool with high-stakes consequences.
However, it was also common in traditional British examinations, where
the experienced task designer recognized the various aspects of challenge
in a task and adjusted the overall difficulty appropriately.
One key to better design is to recognize the importance of tasks in
defining standards. Specific task exemplars, complemented by examples
of various levels of student work on the task, communicate learning and
performance goals in a form that everyone understands.
Since difficulty is a property of the task, not its separate
elements, it can only be reliably determined by trialling the task
with students, and recognizing student responses at different levels in
the scoring scheme. Thus any valid level scheme should be based on a set
of well-analyzed tasks to which other tasks can then be related through
trialling.
In an earlier paper, On specifying a curriculum (Burkhardt 1990), prepared in the light of experience during the design of the British
National Curriculum, I pointed out that the final version gave no indication
as to the types and balance of tasks that were to represent the performance
goals in Mathematics –
the concepts and skills could be shown entirely in short items, or in
the course of three week-long projects, or in a variety of other task
types in between. I argued that to specify a curriculum relatively unambiguously,
you need three independent elements (see Figure
5):
- The tools in the toolkit of mathematical concepts and skills
- The performance targets, as exemplified by task types
- The pattern of classroom learning activities
They are independent, in that none of them determines the others, and
complementary, each supporting the others.
Currently in both the UK and the US there are attempts to produce improved
models of standards. The extract shown in Figure 6 is
from the 2008 standards of the Qualifications
and Curriculum Development Agency (QCDA) in England (QCDA 2007). Note
the general descriptions of processes and the partial move away from
detailed lists of techniques; but it is clear that any of the criteria
can be interpreted at very different levels of difficulty. The tendency
to narrow the task set remains – the easiest way to test, say, the process
of representation is separately, not as part of solving a substantial
non-routine problem. Since the processes do not change much across ages
and levels – it is easy to find tasks that a typical 7 year old can do
(~Level 2) that involve these processes –the focus tends to remain on
the content descriptions at each level (Figure 6, page
2).
Currently in the US, a different kind of model is being developed for
the draft “College and Career Readiness Standards for Mathematics”, commissioned
by the Governors of US states as model national standards (NGA, CCSSO 2009). This draft describes mathematical practices and principles in
broad terms (see Figure 7). Notably, it avoids detailed
lists of technique, replacing them with a relatively rich set of tasks
(see Figure 7, page 2), covering a broad variety
of task types, that exemplifies the range of performance being sought.
Its progress through the dynamics of each state’s education policy formation
will be interesting.
5
2C The inadequacy of professional
development strategies
6
The importance in educational improvement of professional development for
teachers is generally accepted. However fierce their disagreements on other
matters, all agree that improvement in the quality of teaching is essential
for progress, and that professional development has a key role to play. Every
school system has a program (though, when funds are tight, the argument “We
want our best teachers in the classroom” is regularly used to sideline it).
There is a wealth of literature on the evaluation of professional development.
Classics include Guskey (2000, 2002), Joyce & Showers (1980; 1995) and
Loucks-Horsley et al. (1998), Cohen et al (2001). However despite the recommendations
from literature, such evaluation is not often designed to provide the kind
of feedback needed for the effective design of professional development programs,
which requires: well-defined PD designs; observation of the fidelity of their
implementation; and detailed observational feedback on teacher classroom
behaviour.
Aside from academic researchers, it seems rare for anyone to look for evidence
of changes in the behaviour of teachers in the classroom following a professional
development program; yet it seems clear that such changes should be the core
goal of professional development. Why this mismatch? The dominant approach
reflects ‘the professional principle’ – that teachers take whatever they
value from the professional development experience, and that it is not appropriate
for one professional to question the judgment or skill of another. This leads
to a design approach that seeks ‘a civilized discussion between fellow
professionals’. Though this approach may
work well over a long period for some teachers, the limited range of teaching
strategies shown by most teachers suggests that it is inadequate for most.
Those, including ourselves, who have compared teachers’ behaviour in their
classroom, before and after specific programs, commonly find no observable
change. Again why? Professional development programs are usually evaluated
by their designers with questionnaires on how far the teachers found the
experience valuable – a useful but very different outcome. As ever, feedback
has a strong influence on design – programs are designed to be enjoyable
for participants, and most do well in this regard. Such a mismatch between
the main goals and evaluation criteria exemplifies poor strategic design.
Design challenge
While general pedagogical principles are important in teaching, good teachers
also show a wide spectrum of specific high-level skills and teaching strategies.
One characteristic, for example, is ‘role-shifting’ (Phillips et al 1988).
Here the students take more responsibility for their own learning and performance,
adopting traditional teacher roles (manager, explainer, task-setter). The
teacher adopts facilitative roles (adviser, fellow-student, resource), talking
less and asking more open and more strategic questions. However the need
in this approach to follow students’ reasoning and to choose interventions
appropriately requires deeper understanding of both pedagogy and the subject.
Designing professional development that will enable typical teachers to acquire
these new skills is a design challenge.
Over the last few decades, programs that adopt a more skills-focused
approach have been developed. The Bowland Maths Professional Development
modules (Bowland, 2008) illustrate this - see Figure
8 for an extract from one of the modules. They are based on supporting
teachers in trying specific new activities in their classrooms, and reflecting
on the experience. General principles are inferred from a sequence of
such successful experiences – constructive learning for teachers. Observation
shows that teachers make the intended style-shifts, extending their range
of classroom strategies and skills – though not surprising, since this
is the focus of the design, it is valuable nonetheless. Less clear is
how much experience of this kind is needed before teachers carry over
these skills into their everyday practice.
This model has been outlined only to show that it is possible to design
effective professional development – and that better strategic design
and more powerful development methods can both contribute to this.
3. Features of poor strategic design
3
Strategic design is about ensuring that the product interacts effectively
with the system it aims to serve. The examples in Section 2 show lack of
understanding of important aspects of the way the system works: that teachers
teach to tests; that the difficulty of a substantial task is greater than
that of its elements; that discussion of principles is not enough to enable
most teachers to acquire new pedagogical skills. When the design ignores
such properties, the products may be expected to fail and/or to have undesirable
consequences. In this section we explore how this happens, and why it is
so common. We start with a few observable surface features, before looking
at underlying causes. Such features, illustrated in the above examples, include:
- Unintended consequences are a universal feature of poor strategic
design. Policy makers assume that their initiatives will achieve their
goals without negative side effects. Governments and their educational
advisers regularly deplore “teachers teaching to the test”. Curriculum
specifications are always intended to raise real standards. Professional
development programs are only funded because they will forward their goals.
Yet such unintended consequences have usually been predicted, by professional
designers and some others.
- Faith in “expert” advice is an equally common feature of poor
strategic design. Policy makers believe that, if they gather together “some
of the best minds in the field”,
the advice they receive will enable them to achieve their policy goals.
That is a natural assumption in their world. Thus tests, standards, and
professional development have traditionally been delivered in this way.
The reasons it does not work are discussed below.
- Neglect of “gaming” Government initiatives are invariably introduced
by presenting a set of admirable intentions with which few would quarrel.
However, there is little awareness that the rhetoric will be much less
influential than specific changes that promise to impact on those involved
– “teeth” bite, while talk can and will be ignored. Thus everyone concerned
is likely to “game” the system from their own perspective,
while Government assumes that the spirit of the change will be
sustained, however threatening the detail.
Underlying causes
1
Beyond these observable features, what can we say about the causes of poor
strategic design? Our understanding of any human system as complex as education
will always be incomplete, but there are several common elements in strategic
designs that undermine effectiveness.
- Underestimating the design and development challenge is an obvious
corollary of the mismatch between intentions and outcomes that is shown
in the usual failure to achieve the planned positive goals, as well as
the unfortunate unintended consequences. Put simply, policy makers and
other funders often fail to recognize that there is a strategic
design problem, that what they want involves more than the straightforward
application of the experience of good practitioners. Thus professional
design groups regularly face the task of persuading clients to modify the
specification so as to increase the chance that the product will achieve
their goals.
- Timescale mismatch The timescale of politics (a year or two)
is shorter than that needed for the design and development of substantial
innovations, let
alone that of implementing real educational improvement (a decade or two).
Good design and development takes time, so there is often a conflict with
system leadership’s wish for quick results.
- Imbalance between pressure and support When human beings are
asked to do something new, they usually need tools, training and other
forms of support to become proficient. For professionals this is particularly
important when the change is profound, challenging their beliefs as well
as their well-grooved habits of day-by-day practice (see e.g. Fullan 1991).
The mathematics teacher trying for the first time to handle discussion
in the classroom in a facilitative, non-directive way needs effective help,
as does the typical test designer trying, for example, to develop new types
of science problems that students will see as relevant to their everyday
lives.
Governments, however, make policy then apply pressure of various kinds
to ensure that it is implemented. Underestimating the challenge, less attention
is paid to the design, development and provision of support that will enable
those involved to implement the policy effectively. The need for support
is recognized but what is needed is not realistically evaluated; since
effective support tends to be much more expensive than pressure, the need
is underestimated. Further, since design and development of effective materials
would delay implementation, they hope that “the market will provide” –
and, at some level, it will. As for professional development, often an
arbitrary sum is allocated for support and its design within this is left
to those involved in implementation of the policy.
- Casual commissioning Underestimating design and development
challenges leads governments and some other funders to underestimate the
importance of the commissioning process. On the one hand, they try to specify
in too much detail aspects of the design that need to be explored; on the
other, often driven by wanting the product urgently, they fail to ensure
that the emerging design meets the objectives they had set out. Equally,
the selection of the design team is often too casual. A sense of urgency
and cost concerns preclude sensible procedures like asking two or three
groups to produce outline designs (Burkhardt 2008) along
with some trial data on them.
- Unrealistic pace of change Governments often want to be seen
to be “solving the problem”, moving swiftly to the end goal – through the
introduction of a new curriculum, for example. A one-step approach with
a clear end point has advantages. However, the size of the step is limited
by how much change those involved can absorb and implement with the support
provided through tools and collegial support through networks. Often, the
support is less than anticipated, the changes in practice are not made,
and the design intentions are undermined.
The alternative gradual change approach defines a direction of
change but adjusts the pace to be digestible. Well-engineered replacement
units can support profound changes in short bursts. Professional development
aims for specific improvements in practice. The main disadvantage of this
model is not its speed, which can easily meet the decade timescale of real
change, but its lack of glamour – a ‘big bang’ change can inspire both
society and (some) professionals.
- Political need “to be seen to be doing something” In this media-driven
age, where outrage sells better than good news, politicians are constantly
bombarded with ‘public’ demands to improve this or that, or to “make sure
that this can never happen again”. If examination results improve, the
exams are getting easier; if they go down, the education system is to blame.
Governments seek to handle this challenge with a string of initiatives to
show that they are active in meeting society’s, or is it the media’s, wishes.
This is potentially a source of profound concern since, from this perspective,
the success of the initiative in meeting its declared goals is irrelevant.
Any comeback will be far in the future when the minister (or even the Government)
will have changed; however any initiative turns out, the media will always
be able to find something to stir public concern. Most of the politicians
I have talked with are not as cynical as this implies but, though they
may be keen to do things well, keeping the media at bay is an absolute
priority.
This last point generalizes – the priorities of the various key groups in
the system that are affected by the product will not be well-aligned. Some
will be resistant to change, or simply want a quiet life. Other groups will
each have active agendas that may be in conflict. Understanding the system
dynamics, and minimizing the impact on the core goals of the design, are
the foundation of good strategic design.
Contributions of education professionals
2
The examples and discussion above may give the impression that bad strategic
design is a monopoly of policy makers. However, the education professions
are a major contributor. The strategic design of innovations in education,
whether for government or other funding agencies, is still usually based
on the advice of groups of expert practitioners. Documents are drafted, circulated
for comment, and revised, then policies are adopted. But in designing an
innovation, such advisers are extrapolating from their own successful experience
to the new area in question – and assuming the changes will work well in
the hands of other, often less expert, practitioners. Because extrapolation
is notoriously unreliable, this craft-based approach can work well for minor
changes but, for substantial innovation, it underlies the limited impact
and unintended consequences that so often occur.
Typical symptoms of the inadequacy of the input of educational advisers
include:
- They never say that something can’t be done – while professional
educational advisers often criticize government initiatives as “the wrong
thing to do”, they rarely say the policy goals cannot be achieved.
- They never say “We don’t know how to do it” – probably because,
if anyone did, the client would find someone else, more malleable even
if less competent.
- They never try to define the time and resources that it will take to
design and develop the tools and processes needed to achieve the policy
goals; the government or funder takes a decision as to the resources it
wants to allocate, to development and to supporting implementation, and
the profession accepts that decision, even if the resource allocation guarantees
failure.
- They ignore system realities of the various kinds described
above.
The contrast with research-based professions, like medicine or engineering,
is stark. There, research-based methods are used to develop solutions to
offer to policy makers, with evidence on their power and limitations. The
designers estimate the support needed for successful implementation of the
policy, and its costs. When something has not been done before, they say
so and estimate the timescale and effort that will be needed to have a good
chance of success in that area. So governments don’t make policies that are
unachievable, or that they cannot afford. (Imagine a research team saying
“We’ll cure cancer in 5 years with whatever funds you choose to give us”
or “We’ll have all our energy from nuclear fusion in 10 years”.) In this
as in other respects, education is more like “alternative medicine” – ever
willing to offer a treatment with good faith but with no solid evidence that
it works.
The methodology gap
3
A common feature of the examples in Section 2 is that systematic empirical
development through trials, before implementation, would have revealed the
sources of failure and might well have suggested improvements in the designs
– the standard methodology of systematic development.
How does this happen, for example, in the UK where Government is formally
committed to evidence-based
policy formation? Indeed, two elements in the standard innovation cycle are
now firmly established as part of government policy making. Using medical
nomenclature, they are:
- Diagnosis: insight-focused research, much of it government commissioned,
regularly provides policy makers with diagnostic information on the strengths
and weaknesses of current practice in many fields, including education.
- Phase 3 trials: pilot field testing of treatments before implementation
for evidence on outcomes is Government policy; however, because these strategic
decisions are not seen as a design problem by those who make them, the
purpose of those at every level who take part in these pilots is to show
that the initiative “works”, rather than to learn how to improve it. In
practice, driven by the short timescale of politics and the need to be
seen to be proactive, governments reject only egregious failures.
The key gap in the methodology is a research-based link between these
two elements, namely: Design and development of
initiatives using research-based methods.
This is analogous to Phases 1 and 2 of the development of treatments in
medicine – the initial
small scale Phase 1 explorations leading, in selected successful cases, to
their careful systematic development in Phase 2.
Such research-based design and development involves, sequentially:
- Review of research, of craft-based knowledge, and of earlier
innovations;
- Design, imaginatively exploring a broad range of design possibilities;
- Development through an iterative process of feedback from small-scale
trials;
sifting out at each stage those candidates and aspects that prove less promising.
Piloting in representative circumstances is the final step
before large-scale implementation. Its usual role is a summative validation
of the initiative, rather than providing formative and developmental feedback.
The prior phases of research-based development, too-often by-passed
in education, are where the product is refined through rich and detailed
feedback, its quality and robustness enhanced, and unintended side-effects
discovered.
There is a fuller discussion on how to improve the contribution of educational
research to practice in (Burkhardt and Schoenfeld 2003) and (Burkhardt 2006)
as well as in other contributions to this journal. They point out the many
obstacles in the way of useful research that are placed by the current academic
value system in education.
There seem to be three main reasons for government resistance to such improvements:
- The lack of awareness of strategic design as an issue that needs as much
attention as other aspects of design;
- A reluctance to lose the freedom to make policy decisions based on “common
sense” in response to public pressure and/or political opportunity;
- The greater cost and time that professional design implies, modest though
the cost is in comparison with the costs of implementation.
All these reflect the belief, widely held in politics and the media, that
education is an area where specialized knowledge is needed only for details.
“After all, I went through the system and look what it did for me” is a common,
usually unspoken, feeling.
4. Successful strategic design: some examples
4
In this section I outline four initiatives where the strategic design appears
to have played a substantial part in their success. This will help to balance
the gloomy picture painted so far, showing that effective strategic design is possible,
and will inform the discussion of principles for strategic design in Section
5. In selecting these examples, I have looked for designs that combine:
- Educational ambition, breaking new ground in the system they serve;
- Some large scale impact (compatible with the goals!);
- Influence on designs that followed; and
- Are in English (with apologies to heterophones).
In each case, there are links and references to more on the materials, including
examples.
4A Nuffield A-level Physics
1
This course set out to engage 16-18 year old UK students with the processes
of scientific investigation, and to bring some of the major innovations of
20th century physics into school. The origin of this project lay in concerns,
common after Sputnik in 1957, about the state of science education and the
shortage of scientists. In the absence of a national curriculum specification,
this context gave the team freedom to innovate, with success or failure measured
by the level of voluntary participation by schools.
In Issue 1 of this journal, Paul Black
described the thinking and the effort behind the project, including its strategic
design as well as the new and ambitious educational goals and the tactical
and technical design moves that were devised to achieve them (Black, 2008).
So here I shall be brief, simply bringing together the main strategies.
- The course was developed in collaboration or consultation with the key
constituencies, including university physicists, experienced science teachers,
both as team members and as participants in trials, schools that would
trial the course, equipment manufacturers, publishers, teacher trainers,
school district authorities, an examination board, and the funding agency
– the Nuffield Foundation.
- A radically new type of A-level examination was developed, reflecting
the innovative nature of the course. The unprecedented number of components
ranged from a multiple-choice test through more extended examination tasks
to a student report on an individual experimental project.
- Since entry to university in England largely depends on the results of
A-level examinations, negotiations ensured the wide acceptability of the
new examination, in particular for university admissions. The government
body charged with oversight of the examinations had also to agree.
- The construction of the course was seen as a piece of engineering, a
job to be done despite inadequate knowledge of how some of the basic components
in the learning process work.
- Two years of trials in a group of schools provided vital feedback, not
only for the detailed design, but for acceptability by teachers, and for
getting the timing right. These trials did result in some big changes to
the original plans.
While the content of the course, which challenged the existing norms for
curriculum, pedagogy and examinations, was the core of its success, these
strategic elements in the design seem equally essential.
The project had major impact on physics teaching in and beyond the UK. The
course and its examination continued for over 25 years, with a related successor
now in use. It pushed back the boundaries of what was seen to be possible
in school physics, bringing in quantum mechanics and thermodynamics. The
project influenced the subsequent development of many more conventional syllabuses
and textbooks.
4B Connected Mathematics
2
This course was designed to improve the teaching and learning of mathematics
for US students aged 11 to 14. It was developed through a multi-year project,
involving at its peak 12 full-time-equivalent people in the design team.
It was funded by the US National Science Foundation, as one of 13 projects
that aimed to realize the goals set out in “The NCTM Standards” (NCTM, 1989).
Developed by the National Council of Teachers of Mathematics as part of a
national concern at the quality of mathematics education, these standards
set out learning, teaching and assessment goals for school mathematics across
the age range 5 to 18.
Connected Mathematics (CMP), as its name implies, pays particular
attention to tactical design issues, including the coherence of, progression
in, and connections between the various aspects of mathematics. The curriculum
materials build on the authors’ decades of experience in prior projects.
The contribution in this issue (Lappan, Phillips, 2009) by its lead designers, Glenda Lappan and Elizabeth Phillips,
sets out the thinking behind their approach and the way they worked.
The strategic design of this and the other NSF-funded mathematics projects
followed a standard US model involving: several iterations of planning, design,
development, field-testing, and evaluation, followed by publication, marketing,
and support – with regular revision to provide new editions.
Some of the design challenges they faced are universal:
- How far can one incorporate changes in the way mathematics is done outside
school (using calculators and computers for most routine procedures, for
example) and the research findings from the cognitive science and mathematics
education on student learning, while remaining acceptable to a society
that has a traditional picture of “school math”?
- How far can one demand higher-level teaching skills and still serve current
teachers? What support for professional development should one assume?
Other challenges are peculiar to the US, and to this project – for example:
- While in most societies any innovation will face traditionalist counter
pressures (and probably should, as a test of its worth), in US mathematics
education there is a particularly well-organized, well-funded lobby that
attacks any sign of reform.
- Unlike the other three cases in this section, the designers were unable
to significantly influence the high-stakes tests that are used for school
accountability in all US states, with the usual strong influence on classroom
activities. The research indicates that students in schools using CMP perform
at least as well on such tests as comparable groups in more traditional
curricula but the much higher performance in the extra dimensions of understanding
that CMP enables is not assessed or, therefore, publicly recognized.
- Particular attention had to be paid to the listed requirements of the
large “adoption states”, notably California and Texas, where approval is
important for direct impact, influence on other states, and commercial
viability through sales. These requirements are often far from coherent,
reflecting the diverse wishes of the different groups on the committees
that compile them. They always add up to far more than any teacher could
teach, let alone students learn –
altogether a designers’ nightmare that has gotten worse as individual school
districts impose “pacing guides” that, week by week, say when each topic
should be taught and tested.
- The materials were published and offered for sale in competition with
many other curricula, including the four other NSF-funded middle school
curricula, some of which have strong features, as well as the traditional
curricula that have long dominated the market. (These might be seen as
‘comparison groups’.)
In spite of these formidable challenges, CMP has achieved major impact on
US schools. It has a substantial share of the market and is central to any
discussion of middle school mathematics education. What are the factors behind
this success?
- Inherent quality of the material All authors will say that this,
the tactical and technical design, is the key to success. One would like
this to be true, and the quality of CMP is widely acknowledged. On the
other hand, the traditional curricula that have dominated the market, and
still have a large share, succeed despite their only obvious virtue being
familiarity to the customer and client groups.
“That’s the proper way to teach math, like when I was at school.”
- Quality of the design team The success of the Connected
Mathematics curriculum, which is written for both teachers and students,
reflects the diverse talents of the design team. The team consisted of
authors, graduate students, graphics designers, teacher collaborators,
researchers, and an advisory board made up of mathematicians, mathematics
educators, teachers, administrators, and parents.In addition, consultants
from the sciences, engineering, reading, English language learners, and
special education provided valuable insights for specific aspects of
the curriculum.
- Understanding and growing a “niche market” The authors have
long been at the heart of the main organizations in US mathematics education,
not only NCTM but NCSM, the smaller organization of “math supervisors”
in school systems who strongly influence the choices of materials. This
has given them a deep understanding of the needs and constraints perceived
by these key constituencies. This has informed the design of CMP. Those
who were looking for real change, long advocated within this community,
found a workable curriculum that met their ambitions.
- Specific support for meeting strategic challenges The project
recognized the challenges that implementation presents and offered
specific guidance and support. Figure 9 shows examples
of this in CM materials.
- National evaluation Driven by the ”math wars” controversy,
the Bush administration commissioned an evaluation of the available
curricula. An
expert group (not, on this occasion, pre-selected to produce “the right
result”) rated Connected Mathematics as exemplary.
The future will show how far the continuing counter-campaign will succeed,
or whether CMP will provide the new base from which further advances
can be built – for example, in the fuller integration of IT, and the
delivery of functional mathematical literacy.
4C VCE Mathematics
3
In the late 1980s, the Victoria Certificate of Education was introduced
to all Victorian schools as a single pathway for all students to complete
secondary school and, at the same time, as a way in which universities could
select students for particular courses of study. The VCE was designed as
a course of study to be taken over two years in a range of subjects, constructed
according to the same set of principles and accredited by a single authority
representing government and other key stakeholders.
Assessment within the VCE would be a mix of school-based assessments and
end-of-year examinations. Under the Mathematics Study Design, the course
had to provide time for teaching and learning in:
- The development of standard skills and applications;
- Problem solving, applications and modeling (hereafter called problem
solving); and
- Mathematical investigations (hereafter called projects);
Students had to demonstrate that they had worked on all these ‘work requirements’
in both Years 11 and 12. For all final year (Year 12) mathematics courses,
the assessment balance was set at 33% for school assessed coursework and
67% for end-of-year externally set and externally graded examinations. Students’
work was assessed by their teachers and the results were moderated by groups
of teachers from nearby schools. Here we report only on those changes related
to the introduction of problem solving and projects.
VCE mathematics took a fresh look at the range of types of performance
that are important in mathematics, and developed ways to assess the expanded
range in a high-stakes assessment. The design of the problem solving
and modeling coursework broke new ground in many ways. While
the timed examinations were based on standard task types, the VCE included
the following innovative features:
- Mandating that, as part of the assessment, students tackle non-routine
problems and mathematical investigations (‘projects’) in both pure mathematical
and real world contexts;
- Providing substantial time for these tasks, both in class and at home,
with strict protocols for teachers to authenticate that the work done outside
examination conditions had really been done by the student;
- Providing each year new ”starting points” and “themes” for problem solving
and modeling tasks and projects that were compulsory for students to work
on – on the one hand these gave students the opportunity to define their
own specific problems and solution paths and, on the other hand, ensured
some mathematical depth in the topics involved;
- Developing criteria for scoring students reports on their problem solving
and projects, along with systems for teachers to moderate results across
schools; and
- Designing a test to authenticate coursework.
In the early years of the new examination, students had to undertake a 20-hour
mathematical project over 4 weeks, and an 8-hour problem solving task over
2 weeks in each mathematics subject;
this was later changed because of workload so that there was only one of
these tasks for each subject.
The genesis of this innovation involved people who were at the forefront
of Australian developments in mathematics education. Ross Turner and later
Max Stephens managed the design and implementation and smoothed its passage
into reality, always a challenge for innovative high-stakes assessment. (VCE
results are a key factor in university entrance decisions.) Susie Groves
and Kaye Stacey had
pioneered the introduction of problem solving into teacher education at Burwood
College, now in Deakin University, with “The Burwood Box” and associated
teaching materials for schools (Stacey and Groves, 1985). Both were seconded
to the examination board to develop the very substantial written support
materials, which explained the new processes of problem solving and modeling
to teachers. When concerns from universities about standards and authentication
demanded revisions, Peter Stacey and Barry McCrae played a leading role in
the re-design process, including the authenticating test.
For about the first decade of VCE Mathematics, the assessment tasks were
developed each year by groups including university mathematicians, mathematics
educators and practising teachers, and provided to schools by the central
assessing authority. They showed teachers the activities that were important
for students to engage in, and provided topics that contained substantial
mathematical content related to the course material. Sample scripts at each
grade level, marked and annotated, were supplied to ensure consistent marking
by teachers and assessment supervisors.
Figure 10 shows a brief example of a state-provided
theme for an “Investigative project” on mathematical modeling and rates
of change, with one of the starting points that students could choose
for the 20-hour project for the main calculus and functions subject. Figure
11 shows the complete task and instructions for another theme, Maxima
and minima. Note that the starting points have a structured part (a),
but encourage students to work independently and to follow their own
paths in part (b). Students would work in class to begin the project
then, over 4 weeks in class and at home, would carry out the investigation
and prepare the report. Students would report regularly to their teacher
to provide evidence that they were working on the projects themselves,
and finally submit a report of about 10 pages for assessment. Figure
12 shows the criteria for teachers to use in assessing student work
including an assessment checklist and grade descriptors.
Some teachers and students found the experience of the project stressful,
and indeed some misunderstood the nature of mathematical investigation
so wasted time preparing extraordinarily visually attractive reports
with minimal mathematical content. However, for many teachers and students,
these activities provided an unsurpassed mathematical experience. Stacey
(1995, p 66) quotes one very experienced teacher as saying: “I have never
seen such intense, creative and cooperative work in mathematics. In class,
there was a great deal of discussion, yet they were all working on their
own problems.”
Figure 13 shows three examples of the “problem
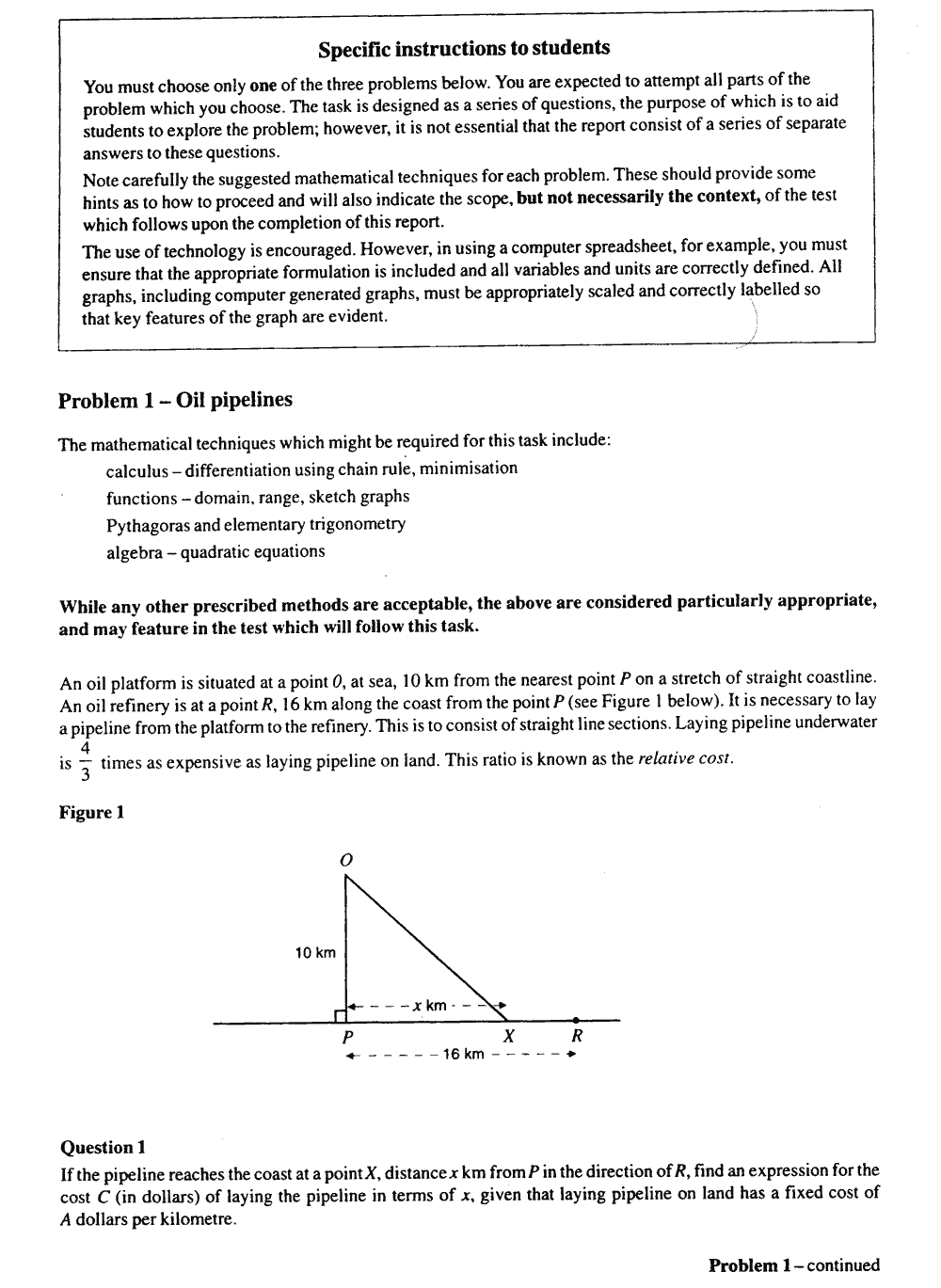
solving task”: Oil pipelines; Through the fog; Rational points on
curves. Designed for 8 hours work, in and out of class, these tasks
recognized that students require time to conduct substantial mathematical
problem solving of a non-routine nature. Since these tasks are more structured
than the projects, providing a set of non-routine questions for students
to tackle, they give students less opportunity to follow their own paths.
Public concern grew in the first years that some students were getting
unauthorized help – with (unsubstantiated) rumours of “buying solutions
in the market”. Protocols for teachers to monitor each student’s progress
worked well in many schools, but in the high stakes environment, suspicion
about cheating lurked.
This problem was solved by the introduction of an interesting innovation
– a short timed test (again centrally set) on the main mathematical ideas
involved in the solution of the problem, given to students after their
reports were handed in. Figure 14 shows the test
for students who had tackled Through the fog. Students whose
performance on the test did not match their performance on the 8-hour
task were called for interview by teachers and principals, where they
were given another opportunity to demonstrate their understanding of
the mathematics in their reports. This process worked very well, and
restored public confidence in the assessment (McCrae, 1995; Stephens & McCrae, 1995). Teachers were supported in the assessment challenges through published
support materials, including task-specific criteria and mark schemes
(Figure 15 shows the criteria for Oil Pipelines)
illustrated with student work.
What were the features of strategic design behind this success?
- Changing a high-stakes examination The research study described
below (Barnes, Clarke and Stephens, 2000) shows how the change in the high-stakes
examination led to corresponding changes in classroom practice throughout
secondary school.
- A fine balance of ambition and realism The changes sought and
achieved were very ambitious, reflecting a world-wide consensus on best
practice in school mathematics in a form that was (and is) rarely found.
- Development from feedback The curriculum and assessment authority
was prepared to fine-tune the design to make it work.
- A consensus for change in the system The changes in VCE were
mandated by the system as a whole; this design team used the opportunity
provided by a climate in which “the status quo was not acceptable”.
- Tests as a monitoring device Assessing and authenticating extended
pieces of student work is always a challenge. Tests have been used in various
ways as part of this process; the use here as a monitoring device was both
original and effective in restoring public confidence.
In an associated research study, Barnes, Clarke and Stephens (2000) looked
at changes in what happened in school classrooms following this change in
high-stakes assessment. This compared classrooms in Victoria with those in
New South Wales where, though the rhetoric promoting problem solving was
similar, there had not been corresponding reforms in assessment. They found
that problem solving activities involving mathematical tasks of the kind
introduced into the tests were introduced into classrooms, not only in the
final year but throughout the secondary schools involved – though, in the
lower grades, perhaps more in form than in substance. David Clarke wrote:
“Most striking in this analysis, was the evidence in Victoria of the ‘ripple
effect’ (Clarke & Stephens, 1996), whereby the language and format
of teacher-devised assessment tasks employed in grades 7 to 10 in Victorian
schools echoed their officially mandated correlates in the 12th grade VCE
to an extraordinary level of detail. ”
The classroom visibility of problem solving activities and assessment emerged
as the key difference between the two states.
Because it tracked changes, this study is important in providing
evidence of a causal connection between task types in high-stakes
assessment and activities in the implemented curriculum – not simply the
well-known similarity of the two (see section 2A).
As often happens, the success of this assessment model was ultimately undermined
by outside events – problems in subjects other than mathematics caused the
curriculum and assessment authority to remove any restrictions on the type of
school-based assessment. Gradually, schools decided it was easier to give
assessment that mimicked the remaining examinations, and so the experience
for students of engaging in substantial problem solving and investigations
gradually withered.
Were there weaknesses in the strategic design? Whenever the school-assessed
component was strongly guided by official requirements and material for substantial
investigations was supplied, it went well in the refined system. But when
both formal requirements and support were withdrawn, it was seen as too challenging.
This suggests:
- Task design is critical The system-level decision to give teachers
freedom in the choice of assessment tasks again was a crucial error in
strategic design. In other systems this move has often been justified as
“giving teachers and students freedom for creative work” but, in a high-stakes
assessment, it is no surprise that they give security and predictability
a higher priority. Control over, at least, the range of task-types used
and how frequently the tasks must be changed is central to the assessment
of non-routine problem solving and investigation.
- Performance goals should be spread across task types The designers’
decision to focus the formal examinations entirely on “facts and skills”
and “analysis” (slightly longer but still routine questions) meant that
problem solving and investigations, confined to the school-assessed component,
were vulnerable to the above change. This decision seemed to make sense,
given the time appropriate for substantial investigative activities. (The
case study in section 4D, below, shows that such things
can be assessed to some extent in timed examinations.)
- Support materials are essential Exemplar problems and projects
were important in supporting teachers and students in this new kind of
work; however, they were only developed for Year 12, whereas teachers of
earlier years could have benefited similarly, raising levels of performance
throughout the schools.
A notable feature of this innovation, in comparison with the others in this
Section, is the fluidity of design control. Key decisions were taken by committees
with changing chairs and membership; the coherence of approach that was maintained
over a decade perhaps reflects that of the mathematics education community
in Victoria at that time.
The initiative has had effects in other Australian states that persist,
with some increasing emphasis on real problem solving nationwide (see e.g.
Curtis & Denton, 2003).
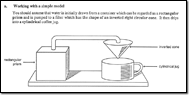
4D Testing Strategic Skills – “The Box Model”
4
This initiative, developed in the 1980s by the Shell Centre with the
largest UK examination board (Joint Matriculation Board, JMB), brought
together in a single package (presented as a box of materials - see
Figure 16):
- A new type of task for a high-stakes mathematics examination – with
five task exemplars, designed to show the variety to be expected in
the ‘live’ examination, with scoring guidance and examples of student
work;
- Teaching materials for three weeks’ teaching, developed to enable
typical teachers to prepare their students for this type of task; and
- Materials to support related in-school do-it-yourself professional
development.
An unusual strategic design feature, compared to the examples outlined
above, was the gradual change model that was adopted. One new
task type was introduced each year, representing:
- One question on the examination;
- 5% of the two-year mathematics syllabus; and
- About three weeks teaching.
Care was taken to remove from the syllabus some topics that took a comparable
amount of classroom time. This approach proved popular with teachers.
They enjoyed the three weeks of new teaching, pedagogically challenging
but well-supported; they were equally glad to get back to more familiar
ground for a while thereafter. They looked forward to the next package.
The first year’s change was the introduction of 15-minute tasks that
assess non-routine problem solving in pure mathematics. The materials,
published as Problems with Patterns and Numbers (PPN, Shell
Centre, 1984), were bought by most of the schools that took the Board’s
O-level examination for age 16 students. The following year, The
Language of Functions and Graphs (LFG,
Swan, 1986) introduced the modeling
of real world situations with Cartesian graphs, and with algebra – graph
interpretation, model critique and formulation are all included. See Figure
17 for exemplar tasks
from both boxes.
Strategically, the initiative was made possible by my membership of
the Research Advisory Committee and the Mathematics Subject Committee
of the JMB, through which a relationship was built that allowed innovation.
I pointed out that, of their list of seven “knowledge and abilities to
be tested” in mathematics (Figure 18), only two
or three were actually assessed by the then-current types of examination
task. I convinced the Board that it was worth improving on this. The
year-by-year change approach was accepted, the Shell Centre found funds
to develop the support materials and tasks for the “live examinations”.
The Board’s chief examiner for mathematics was part of the development
team.
The design and development methodology used is also of interest. The
initial design approach was different in the two cases. PPN was designed
by the Shell Centre team with a group of teachers who were active members
of the Association of Teachers of Mathematics. ATM had, for many years,
pioneered approaches to teaching non-routine problem solving and more
open mathematical investigations. LFG was designed by Malcolm Swan, building
on a decade of Shell Centre research and development work on “translation
skills” (Burkhardt, 1981) by Claude Janvier, Alan Bell and Malcolm Swan
(Janvier 1981, Bell & Janvier, 1981).
One tactical design feature is worth noting. Each of the units demanded
significant changes from the normal teaching style of most teachers.
Non-routine problem solving is destroyed if the teacher breaks the problem
up into steps, or guides the student through the mathematics – yet these
are standard teacher moves when students are having difficulty. Similarly,
LFG is built around classroom discussion in which students explain and
discuss each other's reasoning, not expecting answers from the teacher.
Aware that many teachers would not read extensive notes, we decided that
the essential style changes should be summarized as a few key points
on one page – the inside-back-cover of the teacher’s guide (Figure
19). Feedback from the trials indicated that this worked well. (The
five-session professional development material, which took the teaching
issues further, was probably not widely used in schools – though it was
popular with mathematics advisers for use in professional development
activities that they led.)
The development process was also unusual. The first round of trials was
based on detailed classroom observation by a team of observers of about six
teachers teaching the whole unit. The feedback meetings were based on detailed
reports:
- First, on the style of each teacher, without and with the new materials,
as seen by the observer concerned and any cross-observers; then
- Working step-by-step through the material, all the observers described
what happened in ‘their’ classrooms.
To limit the amount of discussion that so easily runs on when consensus
on design details is sought, I developed the principle of design control
– while empirical feedback and design suggestions are strongly encouraged
by the session chair, there is no search for consensus; feedback is absorbed
and decisions taken by the lead designer of the units, in this case Malcolm
Swan.
This approach to developmental feedback is, of course, much more expensive
than, for example, relying on samples of student work alone. The modules
were an example of “slow design” (de Lange, 2008). Each took about a year
to develop and cost in all around $20,000 per lesson.
These materials had significant impact. The modules were bought by most
of the schools that used this examination. The student responses to the tasks
in the actual examination showed a reasonable range of performance. Since
this was a new area of performance, it is no surprise that the level was
much higher than in the exploratory tests at the beginning of the project.
This kind of ‘switch on’ gain is educationally both valid and valuable –
the students acquired important new skills and the board’s examination reflected
more of their stated goals. There is a lesson in strategic design here. In
contrast to attempts to raise standards in familiar areas of performance
(adding fractions, using percentages, etc.), the introduction of important new areas,
previously missing in examinations, if it is done well almost guarantees
substantial success.
Again, this innovation foundered because of unconnected events – after only
two years, the assessment at age 16 was restructured under larger organizations.
Characteristically, such administrative changes absorb all the attention
and energy of the bodies concerned for several years – working out the new
arrangements and, incidentally, suppressing other innovations. It did not
prove possible to carry over the relationship with the JMB to its broader
successor body (NEAB, now AQA).
When policy makers weigh the likely benefits of reorganization, their speciality,
they rarely recognize the cost – not only in disruption but in stopping ongoing
improvement.
Some of the task types we introduced have persisted in other examinations,
though usually in a more routine form. The “replacement unit” approach to
step-by-step improvement has been successfully used by other designers –
though often without change in high-stakes examinations, limiting the impact.
Comments on these successes
5
These examples show certain common features that may be more general:
- While a funding agency provided the opportunity, the design initiative
came from a group with many years experience and recognized skill in the
design of innovation, a deep understanding of the area they chose, and
knowledge of the results of its long-term research agenda.
- The team was aware of the strategic design challenge and addressed the
needs and concerns of all the key constituencies centrally involved – successfully,
at least for a while.
- Well-aligned changes in the system’s high-stakes assessment, when achievable,
proved a powerful lever for increasing impact.
- Both an immediate “backlash” and a natural process of gradual erosion
are to be expected; reflecting resistance to change, they need to be covered
by persuasive arguments as well as evidence, and by ongoing “engines for
improvement”.
Any innovation in an education system is exposed to political and other
events that will “blow it off course” (in a way that, for example, medicine
and engineering are not). This is likely to remain true unless and until
politicians and the public are persuaded that systematic research, design
and development produces better solutions than the “common sense” that so
often determines policy.
5. Principles for strategic design
5
In this section, I move on from examples and analysis to suggest some
principles for strategic design. While none is essential for substantial,
beneficial, ongoing impact on the system, they each seem to make it more
likely.
Any such principles must, at this stage, be tentative; my hope is that they
will be useful as a focus for the discussion that the paper aims to stimulate.
To that end, I complement the principles with a list of issues – questions
that need investigation as we try to understand better, and to improve, the
interaction of innovative designs and the education systems they seek to
improve. Finally I summarize the top-level goals that this work implies and
some immediate actions that would forward them.
Strategic design principles
1
The following seem to be features of successful examples, while they have
been neglected in the design of other innovations that failed. (They are
phrased in the imperative.)
System awareness: Seek to understand the dynamics of the system
you seek to improve, in all its interacting parts, and use it to guide the
strategic design of the innovation.
Realism: Study the system as it is, not as it is intended to be,
and the forces that shape decisions and actions of all the key groups, from
politicians, parents and the media to teachers and their students; don’t
assume resources that have not been available without valid assurances that
they will be.
Targeting: Be clear and specific about improvement aims, and the
groups of users you are designing for – development should reconcile the
goals and outcomes for those groups.
Alignment: Try to ensure that the set of tools and processes you
develop form a coherent whole, in themselves and in interaction with the
rest of the system – all the key players should be aware and “on board”.
Robustness and flexibility: Since unexpected shocks to your plans
are inevitable, try to design the set of tools and processes so that various
elements can function independently in a range of contexts of use. For example,
design so as to avoid “lethal mutations” (Brown & Campione, 1996) and
to create designs that “degrade gracefully” (Walker,
2006)
Consensus building: Seek consensus on goals and entailments prior
to design and throughout the development process – a profession that speaks
with one voice has more influence on policy than one where diverse opinions
reach policy makers. Consensus does not just happen; it often needs to be
built through explicitly designed processes.
Communication and marketing: Be aware that any large-scale impact
of your work will be influenced by the public, guided by the media. Improve
your communication skills with these groups, and your network of contacts.
Space for excellence in tactical and technical design: Work to
retain as much space as possible for the creative talents in your design
team, and the systematic development that refines the products – good strategic
design is worthless without them.
“We must educate our masters”: Seek to make policy makers, funders,
and designers aware of the crucial role strategic design will play in the
success of the enterprise in turning its goals into large-scale impact.
Big challenges need big teams: The range of skills needed to carry
through a design and development program, with high-quality in all its aspects,
needs to be reflected in the design team – often, particularly for large
scale developments, only a multidisciplinary team can understand and work
with the various communities that will interact with the product.
Strategic design issues
2
At a more detailed level, there are various issues in strategic design which
merit systematic investigation.
Referred to above, they all relate to aspects of choosing a model of
change for an innovation. The appropriate choice will depend on features
of the existing system, and on the resources likely to be available to support
the change. A key variable, usually neglected, is the pace of
change in their practice that the crucial performers (often teachers)
are likely to be able to achieve, without corrupting the intentions of the
innovation – a too-common outcome. Such issues include:
How big a step? How ambitious should a change be? For
a given level of support, if the step is too large, few will take it without
stumbling; if it is too small, why bother? If we are ambitious, can we define
and support a pathway of progress for the key performers, particularly
teachers, so the latter can gradually move to match our ambitions in their
classrooms?
‘Big bang’ v incremental change Should we seek to achieve our goals
as a single major change (e.g. introducing a new curriculum, as in 4A and 4B,
or incrementally, as a planned sequences of changes (as in 4D)?
Small steps can be less expensive, more easily sold, and more digestible
to users. A comprehensive reform is more conventional, and more satisfying
to many, including politicians who like to “solve problems” (though other
fields, like medicine and engineering, move incrementally). The trade-offs
are fairly clear; the best choice less so – and system dependent.
Time scales How can we meet short term political thinking and achieve
anything useful? We have noted the fundamental mismatch between the time-scale
of politics and that of significant educational improvement. Politicians
need to show results well before the next election. Education systems are
built around professionals, skilled in aspects of their work through well-grooved
practices; changes in those practices, particularly those requiring new skills,
take time – for the system as a whole, typically a decade or more. For example,
the recognition in the US in the early 1980s of the need for change in mathematics
education led, through the NCTM Standards in 1989, to the NSF-funded curriculum
projects, whose products began to impinge on the textbook market around 2000
– the process of institutionalization, in which these curricula become the
accepted norm, still continues.
I believe there is opportunity for creative thinking on ways to reconcile
these two timescales. One approach is planned incremental change, which can
provide politicians with a sequence of year-by-year successes to claim within
a decade-long improvement schedule that learns as it proceeds. I expect that
there are others.
Standard slots v new opportunities Should we try to improve an
existing entity (e.g., a school subject or an examination) or to get a new
one accepted, as a replacement or as an alternative? This dilemma has faced
many innovators. For example, statistics education, which has developed internationally
as a problem-based subject built on interpreting real data, has long been
unhappy with being seen as part of school mathematics (though that needs
much more of the same approach!). This discomfort remains but attempts to
get a separate subject slot in the timetable have had limited success. (It
is available as an option in the UK for age 14 upwards.)
That otherwise-excellent book Mathematics and Democracy (Steen, 2001) even suggests that quantitative literacy should
be taught separately from Mathematics – without questioning why society should
give so much curriculum time to a secondary school mathematics curriculum
that is both non-functional and non-motivating for most students, and the
adults they become.
Cross-subject teaching of subjects, though often advocated, has proven even
harder to establish; schools are still organized around subject slots, each
with its own agenda.
The dilemma, and the trade-offs, are clear. Little or no impact in a pure
form versus wider impact of a debased version. Some novel approaches have
been tried, with success on a small scale – for example, a whole-school project
day every week or two. It is worth looking for others.
All these issues of strategic design deserve more study and experiment.
6. Improving strategic design
6
Finally, I propose a set of long and medium term goals, together with immediate
actions that seem likely to forward their achievement.
Long term goals
1
Recognition by policy makers that education can and should become a research-based
field, like medicine where:
- Insight-focused analytic research on working systems is the best route
to diagnosis of problems and their likely causes;
- A long term agenda for improvement is complemented, as in other fields,
by a regularly-reviewed sequence of steps along the way with sensible timescales;
- Good engineering, integrating insights from prior research and development,
design research, systematic development and evaluation in depth, will produce
the most effective solutions;
- Strategic design of their initiatives should be as professional as the
tactical and technical design already (sometimes) are, using the same methodology;
and
- Much better evaluation of products and initiatives in education,
covering in some depth both the various outcomes and the conditions under
which they were achieved.
For this we will need:
- More researchers choosing projects and using methodologies that provide
the in-depth evaluative evidence that policy makers need on products and
processes that are widely available, yielding reliable evidence on “what
works, how well, under what circumstances”;
and
- More people trained in engineering research methods to design and develop
robust solutions.
In mathematics education we will need to learn to emulate science education
in developing:
- Effective machinery for building a consensus on what is needed, and the
steps along that road, leading to;
- Unified recommendations for innovation that reflect government realities.
Medium term goals
2
Recognition by policy makers that (as in health care, for example):
- High-stakes targets (i.e. tests) for (teachers and schools) can distort
priorities, ensuring that the implemented curriculum in most classrooms
is no better than what is tested. The good news (as in Section 4) is the
substantial evidence that better tests can be an effective lever for improvement.
- What is achievable within the timescale required and resources available
is:
- An empirical question that can only be reliably answered by imaginative
design, systematic development and evaluation in some depth;
- Usually much less than is desirable – or is promised by “experts” who
are keen to please government but have no valid evidence for what they
recommend; and
- Will require funding with at least a few–year timescale, involving
competitive design groups and independent evaluation with agreed criteria
and methodologies (c.f. NICE in health care).
- After so many failures from “obviously needed” reforms, there is political
capital to be gained from a sensible research-based approach.
Short term actions
3
Over the next year or two, we can move to strengthen the case for the above
goals by:
- Identifying, as in section 4, examples of successful design, then studying
the various aspects of their strategic design in some depth, and in comparison
with parallel innovations where these are available;
- Identifying, and specifying in some detail, alternative models of change,
analyzing their key features and the expected cost-benefit analysis;
- Refining and strengthening evidence of payoff from giving medium-term
support to high-quality design teams with proven track records in well-defined
areas; and
- Developing effective channels for communication and influence on policy
makers – one of ISDDE’s prime goals to which this journal is a contribution.
There is much to be done to review, strengthen and implement these proposals.
Better understanding of strategic design, and how it interacts with other
aspects will surely be part of it. I believe such an enterprise is worth
increased attention and, insofar as it succeeds, will forward both learning
and teaching and the development of the profession of educational design.
It is worth remembering von Clausewitz’ definition of strategy as the
ability to “make the best use of the few means at our disposal”.
Acknowledgements
ii
The thinking behind this paper has built on discussions over many years
with fellow designers, project leaders and funders. I am particularly grateful
to Phil Daro, Alan Schoenfeld, Mark St. John, Glenda Lappan, Janice Earle,
Quentin Thompson and my colleagues in the Shell Centre, Daniel Pead and Malcolm
Swan. Others, notably Susan McKenney, have provided helpful suggestions.
The limitations are my own.
I hope that responses to this paper will help us collectively to move forward
in our understanding of strategic design, how to improve it, and how to persuade
funders that it is an area of design that needs both imagination and systematic
development.
References
iii
Barnes, M., Clarke, D., and Stephens, M. (2000). Assessment: The
engine of systemic curricular reform? Journal of Curriculum
Studies, 32(5), 623-650.
Bell, A., Janvier, C. (1981) The Interpretation of Graphs Representing
Situations. For the Learning of Mathematics 2(1) pp34-42.
Black, P.J., & Atkin, J. (Eds.), (1996). Changing the subject:
Innovations in science, mathematics and technology education. London:
Routledge.
Black, P. & Wiliam, D. (1998). Assessment and Classroom Learning. Assessment
in Education 5(1) pp. 7-71.
Black, P. & Wiliam, D. (2001). Inside the black box. London:
Kings College
Brown, A. L., & Campione, J. C. (1996). Psychological learning theory
and the design of innovative environments: On procedures, principles
and systems. In L. Shauble & R. Glaser (Eds.), Contributions
of instructional innovation to understanding learning. Hillsdale,
NJ: Lawrence Erlbaum Associates.
Burkhardt, H., (1981). The Real World and Mathematics, Blackie: Glasgow,
revised Nottingham: Shell Centre Publications 2000.
Burkhardt, H. (1990). On Specifying a National Curriculum, in Developments
in School Mathematics Worldwide, Wirszup, I & Streit, R. (Eds.)
Chicago: University of Chicago School Mathematics Project.
Burkhardt, H. (2006). From design research to large-scale impact:
Engineering research in education. In J. Van den Akker, K. Gravemeijer,
S. McKenney, & N. Nieveen (Eds.), Educational design research.
London: Routledge.
Burkhardt, H., & Schoenfeld, A. H. (2003). Improving Educational
Research: towards a more useful, more influential and better funded enterprise. Educational
Researcher, 32, 3-14.
Clarke, D. J. & Stephens, W. M. (1996). The ripple effect: the instructional
impact of the systemic introduction of performance assessment in mathematics.
In M. Birenbaum and F. Dochy (eds), Alternatives in Assessment of
Achievements, Learning Processes and Prior Knowledge (pp. 63-92).
Dordrecht, The Netherlands: Kluwer.
Cockcroft (1982). Mathematics Counts. London: HMSO.
Cohen, D.K., Hill, H.C. (2001). Learning Policy: When State Education
Reform Works. Yale University Press, New Haven, CT
Crowther (1959). Report 15-18 Half our future. A Report of
the Central Advisory Council for Education, HMSO: London.
Curtis, D. & Denton, R. (2003). The Authentic Performance-based
Assessment of Problem-solving. Station Arcade, South Australia:
National Centre for Vocational Education Research.
de Lange, J. (2008). Invited talk at the ISDDE annual meeting. June
29-July 2. Egmond aan Zee, the Netherlands.
DfES. (1988). Proposals of the Secretary of State for the
National Curriculum in Mathematics, Department for Education and
Science, London: HMSO.
Fullan, M. (1991). The new meaning of educational change. New
York: Teachers College Press.
Goodlad, J. (1994). Curriculum as a field of study. In T. Husén, & T.
Postlethwaite (Eds.), The international encyclopedia of education (pp.
1262-1267). Oxford: Pergamon Press.
Guskey, T. R. (2000). Evaluating professional development.
Thousand Oaks: Corwin Press.
Guskey, T. R. (2002). Professional development and teacher change. Teachers
and Teaching: theory and practice, 8(3/4), 381-391.
Janvier, C. (1981). Use of Situations in Mathematics Education. Educational
Studies in Mathematics 12 113-122.
Joyce, B., & Showers, B. (1980). Improving science teaching: The
messages of research. Educational Leadership, 37, 379-385.
Joyce, B., & Showers, B. (1995). Student achievement through
staff development: Fundamentals of school renewal (2nd ed.). White
Plains, NY: Longman.
Loucks-Horsley, S., Hewson, P., Love, N., & Stiles, K. (1998). Designing
professional development for teachers of science and mathematics.
Thousand Oaks, CA: Corwin Press.
MARS (2001). Crust, R., Burkhardt H. and the MARS team. Balanced
Assessment in Mathematics. Annual tests for Grades 3 through 10.
2001–2004. Monterey, CA: CTB/McGraw-Hill; 2005- Nottingham: Shell
Centre Publications
McCrae, B. (1995). An evaluation of system-wide assessment of problem
solving at Year 12 by report and related test. In Proceedings of
the 18th Annual Conference of MERGA.
NCTM (1989). Curriculum and Evaluation Standards for Mathematics,
National Council of Teachers of Mathematics, Reston VA: NCTM
NGA, CCSSO (2009). Common Core Standards Initiative,
National Governors Association/Council of Chief State School Officers,
Washington DC.
http://www.corestandards.org/ Retrieved November 2009
Phillips, R.J., Burkhardt, H., Fraser, R., Coupland, J., Pimm, D., & Ridgway,
J. (1988). Learning activities & classroom roles with and without
the microcomputer. Journal of Mathematical Behavior, 6, 305–338.
Plomp, T. (1982). Onderwijs technologie: Enige verkenningen [Educational
technology: Some explorations]. Inaugural address. Enschede: University
of Twente.
Schoenfeld, A. H. (1985). Mathematical problem solving. Orlando,
FL: Academic Press.
Schoenfeld, A. H. (2002). Research methods in (mathematics) education.
In L. English (Ed.), Handbook of international research in mathematics
education (pp. 435–488). Mahwah, NJ: Erlbaum.
Shell Centre (1984). Swan, M., Pitt, J., Fraser, R. E., & Burkhardt,
H., with the Shell Centre team, Problems with Patterns and Numbers.
Joint Matriculation Board, Manchester, U.K.; reprinted 2000, Shell Centre
Publications, Nottingham, U.K.
http://www.mathshell.com/scp/index.htm.
Stacey, K. (1995) The challenges of keeping open problem solving open
in school mathematics. Zentralblatt fur Didaktik der Mathematik 95 62
– 67.
Stacey, K. & Groves, S. (1985) Strategies for Problem Solving,
Melbourne: Latitude Publications
Stephens, M., & McCrae, B. (1995). Assessing problem solving in
a school system: principles to practice. Australian Senior Mathematics
Journal, 9(1), 11–28.
Swan, M. with the Shell Centre team: (1986). The Language of Functions
and Graphs, Manchester, U.K.: Joint Matriculation Board, reprinted
2000, Nottingham, U.K.: Shell Centre Publications.
http://www.mathshell.com/scp/index.htm.
Van den Akker, J., Gravemeijer, K., McKenney, S. & Nieveen, N. (Eds.)
(2006). Educational design research. London: Routledge.
Verhagen, P.W. (2000). Over het opleiden van onderwijskundig ontwerpers.
[On educating educational designers] Inaugural address. Enschede:
University of Twente.
Victorian Board of Studies (1995). VCE Mathematics:
Specialist – Official Sample CATs. Blackburn: HarperSchools.
Walker, D. (2006). Toward productive design studies. In J. van den Akker,
K. Gravemeijer, S. McKenney & N. Nieveen (Eds.) Educational design
research. London: Routledge.
Footnotes
iv
[1] The contrast with medicine,
for example, is stark. One cannot imagine penicillin getting lost.
[2]Apart from their military
connotations, these terms parallel those that Alan Schoenfeld coined in
his analysis of mathematical problem solving (Schoenfeld, 1985). This is
appropriate because design is a type of problem solving. Schoenfeld
added a fourth metacognitive aspect, control – the monitoring
and guiding of the problem solving process – which is reflected in design
control..
[3] I have mainly contributed
to the other aspects.
[4] I will say little about
this important area because, particularly in mathematics education, the
choice of learning goals is often confused with the pedagogical question
of how that learning should be achieved. The latter is the focus of most
of the controversy.
[5] The description of
the camel as “a horse designed by a committee”, while a slander on that
admirable beast, captures this important point.
[6] “Goodhart’s Law” states
that “when a measure becomes a target, it ceases to be a good measure”
– essentially because targets promotes gaming and other distortions described
here. Dylan Wiliam’s version is “The higher the stakes, the worse the assessment”.
There is evidence here that this, while commonly true, is not inevitable.
[7] Ironically, what usually
happens in practice is the reverse of parents choosing schools for the
kids; because of limits of capacity in each school, popular schools choose
their students.
[8] In health care it is
now well-recognized that unbalanced targets distort clinical priorities.
For example, an earlier emphasis in the UK on reducing maximum waiting
times led to the treatment of some more urgent cases being delayed.
[9] If an English Language
test were relabeled Mathematics, its psychometric “reliability” would be
unchanged. The statistical tools used measure consistency and levels of
difficulty; they say nothing about what is being assessed.
[10] The Cockcroft Report
(1982) defined the purpose of good assessment in these terms.
[11] I have avoided the
standard terms, validity and reliability, because their
usual non-technical meanings are distorted to allow statistical
definitions that amount simply to consistency – between individual
items and the test and between supposedly equivalent tests.
[12] When the National
Curriculum was being developed, a senior UK policy maker said to me: “Well,
with maths, it’s things you can either do or you can’t, isn’t it?” and
went on to impose this checklist approach on the Working Group. For English
Language, which politicians and policy makers understand much better, essays
and other extended writing, not just vocabulary lists and grammar rules,
are central in both the standards and the tests. There are no substantial
tasks in the Mathematics standards or tests.
[13] Though more sophisticated
concepts, such as the formalism for arithmetic progressions, can be used
profitably in this task, most of the interesting results can be found without
them – and few 16-year–olds can use them in non-routine problems, even
when they can in routine exercises.
[14] For example, examination
tasks in Euclidean Geometry consisted of two parts: a “proof” of a theorem
that the student was expected to have learnt, followed by a “rider” that
involved using the theorem, among other things, to solve a non-routine
extension.
[15] This approach implicitly
recognizes the weakness of models of performance based entirely on analytic
descriptions of the elements of the domain. However, many in authority,
inside and outside the field, find it surprisingly difficult to accept
specifications that are partly based on exemplars.
[16] 40 pages of varied
task exemplars (typically 5 to 20 minutes) were included in the original
version of the National Curriculum (DfES 1988), designed by the Government’s
Mathematics Working Group and circulated for comment. The removal of the
exemplar tasks from subsequent revisions was never explained; it was probably
their lack of one-to-one alignment with the detailed level criteria. The
length of each of the test items that emerged is about 90 seconds.
[17] A comforting phrase
that is often used in England.
[18] For example, some
schools exclude students from the high-stakes Grade 12 A-level examination
in those subjects where they did not do well in the Grade 11 AS examination,
even though that subject may be important to a student’s future plans.
[19] Jan de Lange, at
the 2008 ISDDE Egmond conference, used the phrase “slow design” as the
route to excellence.
[20] As in
architecture, where competitions for important buildings are common.
[21] The UK Government
had a ‘grid’ system across the various departments of state designed to
ensure that there was a new announcement every few days to keep the media
happy.
[22] In an example from
health care of political decisions under outside pressure, the USA and
New Zealand allow pharmaceutical companies to market their drugs directly
to consumers. Patients, despite their lack of diagnostic expertise, are
increasingly demanding certain treatments.
[24] I am not trying
to suggest that all medical procedures are research-based but the ongoing
movement in that direction is a good model for education. (In both fields,
practitioners also respond to societal demands, however unfounded – e.g.
antibiotics for virus infections, long division by hand!)
[25] I am grateful to
the lead designers for their help the with facts; the analysis is mine.
[26] The Nuffield Foundation
has a remarkable record of successful innovation in science education.
The Foundation has always paid attention to the system issues involved.
[27] At that time students’
A-level certificates bore the signature of the Secretary of State!
[28] They were awarded
the ISSDE Prize for Educational Design in 2008 for Connected Mathematics.
[29] Broader spectrum
tests are available (MARS, 2000–) and are used in some school
districts, mostly in California, in addition to the state tests. Their
influence has been mostly indirect.
[30] This is one reason
behind the comment that US curricula tend to be “mile wide, inch deep.”
[31] The customer, usually
the school district leadership, makes the decision to buy materials; the
clients, teachers and students, use them.
[32] In the absence of
the substantial empirical effort that, as in medicine, would be needed
to collect reliable evidence, this was the usual “evaluation by inspection”.
[33] Mathematics was
broken into four “subjects”; students would choose at most two a year.
[34] Their work had been
recognized in their appointment by the International Program Committee
of the 5th Internal Congress on Mathematical Education as Australian Organizers
of the Problem Solving theme at the 1984 Adelaide Congress (Alan Schoenfeld
and I shared this with them).
[35] Malcolm Swan, the
lead designer, was awarded the ISSDE Prize for Educational Design in 2008
for this module. “The Red Box” is still used and talked about across the
English-speaking world.
[36] The second round
of development was conventional. A representative sample of about 30 classrooms
trialled the materials, with teachers reporting back on their experience
and sending sample student work.
[37] Some of these issues
have been discussed in the Dutch literature, e.g by Plomp (1982), Verhagen
(2000), van den Akker, Gravemeijer, McKenney and Nieveen (2006).
[38] The 13 projects
in mathematics supported by NSF, of which 4B is one,
made a wide range of choices – from modest change to near-revolution.
[39] This 25-year timescale,
from an initiation event to systemic change, is not atypical across fields,
exemplified by penicillin and the vacuum cleaner among other revolutionary
innovations.
[40] Variously called mathematical
literacy by PISA and many others, functional mathematics in
the UK, quantitative reasoning, and numeracy (in its
original meaning, see Crowther Report 1959), so often now corrupted
to mean basic skills in arithmetic.
[41] In the UK the National
Institute for Health and Clinical Excellence (NICE) evaluates drugs and
medical procedures for effectiveness and, somewhat controversially, for
cost-effectiveness. Many countries, faced with rapidly rising cost of new
treatments, are considering such systems.
[42] This emphasis is
very different from current fashions in research “quality” (Burkhardt and
Schoenfeld 2003). More basic research should be seen as long term, also
demanding evidence of the generalizability (Schoenfeld 2001) of results
– in particular, how far they are valid and robust in the domain of the
intended design application.
About the Author
v
Hugh Burkhardt has been at the Shell Centre for Mathematical
Education at the University of Nottingham since 1976, as Director until
1992. Since then he has led a series of international projects in the UK
and the US, including Balanced Assessment, the Mathematical Assessment
Resource Service (MARS), and its development of a Toolkit for Change Agents.
He takes an 'engineering' view of educational research and development
- that it is about systematic design and development to make a complex
system work better, with theory as a guide and empirical evidence the ultimate
arbiter. His core interest is in the dynamics of curriculum change. He
sees assessment as one important 'tool for change' among the many that
are needed to help achieve some resemblance between goals of policy and
outcomes in practice. His other interests include making mathematics more
functional for everyone through teaching real problem solving and mathematical
modeling, computer-aided math education, software interface design and
human-computer interaction. He graduated from Oxford University and the
University of Birmingham where, alongside research in theoretical physics
and undergraduate teaching, he first developed his work on teaching the
uses of mathematics to help solve everyday life problems. He remains occasionally
active in elementary particle physics. He founded and is Executive Chair
of the International Society for Design and Development in Education.